WikiDer > Постоянная кручения

В постоянная кручения представляет собой геометрическое свойство поперечного сечения стержня, которое участвует в соотношении между углом скручивания и приложенным крутящим моментом вдоль оси стержня для однородного линейно-упругого стержня. Постоянная кручения вместе со свойствами материала и длиной описывает крутящий момент стержня. жесткость. Единица системы СИ для постоянной кручения - м⁴.

История

В 1820 году французский инженер А. Дюло аналитически вывел, что постоянная кручения балки идентична постоянной второй момент площади нормально к сечению J_zz, которое имеет точное аналитическое уравнение, предполагая, что плоское сечение до скручивания остается плоским после скручивания, а диаметр остается прямой линией. К сожалению, это предположение верно только для балок с круглым поперечным сечением и неверно для любых других форма, в которой происходит коробление.^[1]

Для некруглых поперечных сечений не существует точных аналитических уравнений для определения постоянной кручения. Однако приблизительные решения были найдены для многих форм. Некруглые поперечные сечения всегда имеют деформации коробления, что требует численных методов для точного расчета постоянной кручения.^[2]

Жесткость на кручение балок с некруглым поперечным сечением значительно увеличивается, если искривление концевых участков ограничивается, например, жесткими концевыми блоками.^[3]

Частичная деривация

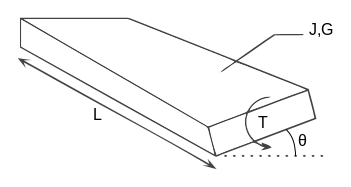
Для балки равномерного сечения по длине:

${displaystyle heta = {frac {TL} {GJ}}}$

куда

${displaystyle heta}$ угол закручивания в радианах

Т прилагаемый крутящий момент

L длина балки

грамм это Модуль жесткости (модуль сдвига) материала

J крутильная постоянная

Торсионная жесткость (ГДж) и жесткость (ГДж / л)

Обращая предыдущее соотношение, мы можем определить две величины: жесткость на кручение

${displaystyle GJ = {frac {TL} {heta}}}$ с единицами СИ Н.м²/ рад

И жесткость на кручение:

${displaystyle {frac {GJ} {L}} = {frac {T} {heta}}}$ с единицами СИ Н.м / рад

Примеры конкретных однородных форм поперечного сечения

Круг

${displaystyle J_ {zz} = J_ {xx} + J_ {yy} = {frac {pi r ^ {4}} {4}} + {frac {pi r ^ {4}} {4}} = {frac { пи г ^ {4}} {2}}}$^[4]

куда

р это радиус

Это идентично второй момент площади J_zz и точно.

в качестве альтернативы напишите: ${displaystyle J = {frac {pi D ^ {4}} {32}}}$^[4]куда

D это диаметр

Эллипс

${displaystyle Japprox {frac {pi a ^ {3} b ^ {3}} {a ^ {2} + b ^ {2}}}}$^[5][6]

куда

а это большой радиус

б это малый радиус

Квадрат

${displaystyle Japprox, 2.25a ^ {4}}$^[5]

куда

а является половина длина стороны.

Прямоугольник

${displaystyle Japprox eta ab ^ {3}}$

куда

а это длина длинной стороны

б это длина короткой стороны

${displaystyle eta}$ находится из следующей таблицы:

а / б	${displaystyle eta}$
1.0	0.141
1.5	0.196
2.0	0.229
2.5	0.249
3.0	0.263
4.0	0.281
5.0	0.291
6.0	0.299
10.0	0.312
${displaystyle infty}$	0.333

^[7]

В качестве альтернативы можно использовать следующее уравнение с погрешностью не более 4%:

${displaystyle Japprox ab ^ {3} left ({frac {16} {3}} - 3,36 {frac {b} {a}} left (1- {frac {b ^ {4}} {12a ^ {4}}) } ight) ight)}$^[5]

В приведенной выше формуле a и b являются половина длина длинной и короткой сторон соответственно.

Открытая тонкостенная труба одинаковой толщины

${displaystyle J = {frac {1} {3}} Ut ^ {3}}$^[8]

т толщина стенки

U длина средней границы (периметр срединного сечения)

Круглая тонкостенная открытая труба одинаковой толщины (приближение)

Это трубка с продольной прорезью в стенке.

${displaystyle J = {frac {2} {3}} pi rt ^ {3}}$^[9]

т толщина стенки

р средний радиус

Это выводится из приведенного выше уравнения для произвольной тонкостенной открытой трубы однородной толщины.

Рекомендации

внешняя ссылка

• Калькулятор постоянной кручения