WikiDer > Усеченная восьмигранная призма
| Усеченная восьмигранная призма | |
|---|---|
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 54 |
| Символ Шлефли | т0,1,3{3,4,2} или t {3,4} × {} т0,1,2,3{3,3,2} или tr {3,3} × {} |
| Кокстер-Дынкин | |
| Клетки | 16: 2 6 8 |
| Лица | 64: 48 {4} 16 {6} |
| Края | 96 |
| Вершины | 48 |
| Фигура вершины |  Равнобедренный-треугольная пирамида |
| Группа симметрии | [3,4,2], порядок 96 [3,3,2], порядок 48 |
| Двойной многогранник | Шестигранная бипирамида Тетракис |
| Характеристики | выпуклый |
В 4-х мерном геометрия, а усеченная восьмигранная призма или же всенаправленная тетраэдрическая призма выпуклый равномерный 4-многогранник. В этом 4-многограннике 16 клетки (2 усеченные октаэдры соединены 6 кубики, 8 шестиугольные призмы.) Имеет 64 грани (48 квадраты и 16 шестиугольники), 96 ребер и 48 вершин.
Он имеет две конструкции симметрии, одну из усеченный октаэдр, и один как омниусечение из тетраэдр.
Это одна из 18 однородных многогранных призм, созданных с помощью призмы для соединения пар параллельно Платоновы тела и Архимедовы тела.
Изображений
 Сеть | 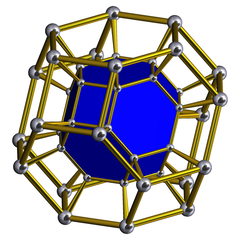 Диаграмма Шлегеля |
Альтернативные названия
- Усеченная восьмигранная диадическая призма (Норман В. Джонсон)
- Усеченная октаэдрическая гиперпризма
- Топ (Джонатан Бауэрс: для усеченной восьмигранной призмы)
Связанные многогранники
В плоскостная тетраэдрическая призма (также называемый икосаэдрическая призма), ![]()
![]()
![]()
![]()
![]()
![]()
![]() , sr {3,3} × {}, связана с этим многогранником точно так же, как курносый тетраэдр (икосаэдр),
, sr {3,3} × {}, связана с этим многогранником точно так же, как курносый тетраэдр (икосаэдр), ![]()
![]()
![]()
![]()
![]() это чередование усеченный октаэдр в своей тетраэдрической симметрии
это чередование усеченный октаэдр в своей тетраэдрической симметрии ![]()
![]()
![]()
![]()
![]() . В плоскостная тетраэдрическая призма имеет симметрию [(3,3)+, 2], порядка 24, хотя как икосаэдрическая призма, ее полная симметрия составляет [5,3,2], порядок 240.
. В плоскостная тетраэдрическая призма имеет симметрию [(3,3)+, 2], порядка 24, хотя как икосаэдрическая призма, ее полная симметрия составляет [5,3,2], порядок 240.
Также связаны полная курносая тетраэдрическая антипризма или же всенаправленная тетраэдрическая антипризма определяется как чередование полностью усеченной тетраэдрической призмы, представленной = ht0,1,2,3{3,3,2} или ![]()
![]()
![]()
![]()
![]()
![]()
![]() , хотя его нельзя построить как равномерный 4-многогранник. Это также можно рассматривать как чередующаяся усеченная восьмигранная призма или же пиритоэдрическая икосаэдрическая антипризма,
, хотя его нельзя построить как равномерный 4-многогранник. Это также можно рассматривать как чередующаяся усеченная восьмигранная призма или же пиритоэдрическая икосаэдрическая антипризма, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Имеет 2 икосаэдры соединены 6 тетраэдры и 8 октаэдры, с 24 неправильными тетраэдры в чередующихся промежутках. Всего у него 40 ячеек, 112 треугольных граней, 96 ребер и 24 вершины. Имеет [4, (3,2)+] симметрии, порядка 48, а также [3,3,2]+ симметрия, порядок 24.
. Имеет 2 икосаэдры соединены 6 тетраэдры и 8 октаэдры, с 24 неправильными тетраэдры в чередующихся промежутках. Всего у него 40 ячеек, 112 треугольных граней, 96 ребер и 24 вершины. Имеет [4, (3,2)+] симметрии, порядка 48, а также [3,3,2]+ симметрия, порядок 24.
Существует конструкция с двумя правильными икосаэдрами в положениях курноса с двумя длинами ребер в соотношении примерно 0,831: 1.
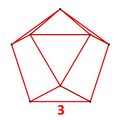
Фигура вершины для всенаправленная тетраэдрическая антипризма
Смотрите также
внешняя ссылка
- 6. Выпуклая однородная призматическая полихора - Модель 54., Георгий Ольшевский.
- Клитцинг, Ричард. "4D однородные многогранники (полихоры) x x3x3x - вершина".
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |
