WikiDer > График Тутте – Кокстера
| График Тутте – Кокстера | |
|---|---|
 | |
| Названный в честь | В. Т. Тутте Х. С. М. Коксетер |
| Вершины | 30 |
| Края | 45 |
| Радиус | 4 |
| Диаметр | 4 |
| Обхват | 8 |
| Автоморфизмы | 1440 (Aut (S6)) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Клетка Граф Мура Симметричный Дистанционно-регулярный Дистанционно-транзитивный Двудольный |
| Таблица графиков и параметров | |
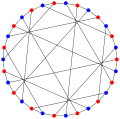
в математический поле теория графов, то График Тутте – Кокстера или Тутте восемь клеток или График Кремоны – Ричмонда это 3-регулярный график с 30 вершинами и 45 ребрами. Как самый маленький кубический граф из обхват 8 это клетка и Граф Мура. это двудольный, и может быть построена как Граф Леви из обобщенный четырехугольник W2 (известный как Конфигурация Кремона – Ричмонд). Граф назван в честь Уильям Томас Тутте и Х. С. М. Коксетер; он был открыт Тутте (1947), но его связь с геометрическими конфигурациями была исследована обоими авторами в паре совместно опубликованных статей (Tutte 1958; Coxeter 1958a).
Все кубический дистанционно регулярные графы известны.[1] Tutte – Coxeter - один из 13 таких графиков.
Она имеет номер перехода 13,[2][3] толщина книги 3 и номер очереди 2.[4]
Конструкции и автоморфизмы
Особенно простая комбинаторная конструкция графа Тутта – Кокстера принадлежит Кокстеру (1958b) и основана на работе Сильвестра (1844). В современной терминологии возьмем полный график на 6 вершинах K6. Он имеет 15 ребер, а также 15 идеальное соответствие. Каждая вершина графа Тутта – Кокстера соответствует ребру или точному совпадению K6, и каждое ребро графа Тутта – Кокстера соединяет идеальное соответствие K6 к каждому из трех составляющих его ребер. По симметрии каждое ребро K6 принадлежит трем идеальным совпадениям. Между прочим, это разделение вершин на ребра-вершины и совпадающие вершины показывает, что граф Тутте-Кокстера двудольный.
На основе этой конструкции Кокстер показал, что граф Тутте – Кокстера является симметричный граф; оно имеет группа 1440 г. автоморфизмы, которые можно отождествить с автоморфизмами группы перестановок шести элементов (Coxeter 1958b). В внутренние автоморфизмы этой группы соответствуют перестановке шести вершин K6 график; эти перестановки действуют на граф Тутта – Кокстера, переставляя вершины на каждой стороне его двудольного деления, сохраняя при этом каждую из двух сторон фиксированной как набор. В дополнение внешние автоморфизмы группы перестановок меняют одну сторону двудольного разделения на другую. Как показал Кокстер, любой путь, содержащий до пяти ребер в графе Тутта – Кокстера, эквивалентен любому другому такому пути с помощью одного такого автоморфизма.
График Тутте – Кокстера как здание
Этот график является сферическое здание ассоциированный с симплектической группой (между этой группой и симметрической группой существует исключительный изоморфизм ). В частности, это график заболеваемости обобщенный четырехугольник.
Конкретно, граф Тутте-Кокстера можно определить из 4-мерного симплектическое векторное пространство V над следующим образом:
- вершины - либо ненулевые векторы, либо изотропные двумерные подпространства,
- есть край между ненулевым вектором v и изотропное двумерное подпространство если и только если .
Галерея
В хроматическое число графа Тутта – Кокстера равно 2.
В хроматический индекс графа Тутта – Кокстера равно 3.
Рекомендации
- ^ Brouwer, A.E .; Коэн, А. М .; и Ноймайер А. Дистанционно регулярные графы. Нью-Йорк: Springer-Verlag, 1989.
- ^ Пегг, Э. Т.; Эксу, Г. (2009). «Графики пересекающихся чисел». Математика журнал. 11 (2). Дои:10.3888 / tmj.11.2-2.CS1 maint: ref = harv (ссылка на сайт)
- ^ Эксу, Дж. «Прямолинейные рисунки знаменитых графов».
- ^ Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- Кокстер, Х. С. М. (1958а). «Хорды неразрушенной квадрики в PG (3,3)». Мочь. J. Math. 10: 484–488. Дои:10.4153 / CJM-1958-047-0.
- Кокстер, Х. С. М. (1958b). «Двенадцать баллов в PG (5,3) с 95040 самопреобразованиями». Труды Королевского общества А. 247 (1250): 279–293. Дои:10.1098 / rspa.1958.0184. JSTOR 100667. S2CID 121676627.
- Сильвестр, Дж. Дж. (1844). «Элементарные исследования в анализе комбинаторной агрегации». Фил. Mag. Серия 3. 24: 285–295. Дои:10.1080/14786444408644856.
- Тутте, В. Т. (1947). «Семейство кубических графов». Proc. Cambridge Philos. Soc. 43 (4): 459–474. Дои:10.1017 / S0305004100023720.
- Тутте, В. Т. (1958). «Хорды неразрушенной квадрики в PG (3,3)». Мочь. J. Math. 10: 481–483. Дои:10.4153 / CJM-1958-046-3.
внешняя ссылка
- Франсуа Лабель. "3D модель восьмерки Тутте".
- Вайсштейн, Эрик В. «Граф Леви». MathWorld.
- Экзу, Дж. «Прямолинейные рисунки известных графов». [1]