WikiDer > Теорема Вивианиса - Википедия

Для любой внутренней точки P сумма длин s + ты + т равна высоте равностороннего треугольника.

Теорема Вивиани, названный в честь Винченцо Вивиани, утверждает, что сумма расстояний от любой внутренняя точка к сторонам равносторонний треугольник равна длине треугольника высота.^[1] Это теорема, обычно используемая на различных математических олимпиадах, экзаменах по математике в средней школе, и имеет широкое применение во многих задачах реального мира.

Доказательство

Наглядное доказательство теоремы Вивиани

1.	Показаны ближайшие расстояния от точки P до сторон равностороннего треугольника ABC.
2.	Прямые DE, FG и HI, параллельные AB, BC и CA, соответственно, и проходящие через P, определяют аналогичные треугольники PHE, PFI и PDG.
3.	Поскольку эти треугольники равносторонние, их высоту можно повернуть вертикально.
4.	Поскольку PGCH представляет собой параллелограмм, треугольник PHE можно сдвинуть вверх, чтобы показать, что сумма высот равна высоте треугольника ABC.

Это доказательство зависит от легко доказываемого утверждения о том, что площадь треугольника равна половине его основания, умноженному на его высоту, то есть половину произведения одной стороны на высоту с этой стороны.^[2]

Пусть ABC - равносторонний треугольник, высота которого равна час и чья сторона а.

Пусть P - произвольная точка внутри треугольника и u, s, t расстояния P от сторон. Проведите линию от P до каждого из A, B и C, образуя три треугольника PAB, PBC и PCA.

Теперь площади этих треугольников равны ${ displaystyle { frac {и cdot a} {2}}}$, ${ displaystyle { frac {s cdot a} {2}}}$, и ${ displaystyle { frac {t cdot a} {2}}}$. Они точно заполняют ограничивающий треугольник, поэтому сумма этих площадей равна площади ограничивающего треугольника, поэтому мы можем написать:

${ displaystyle { frac {u cdot a} {2}} + { frac {s cdot a} {2}} + { frac {t cdot a} {2}} = { frac {h cdot a} {2}}}$

и поэтому

${ displaystyle u + s + t = h}$

Q.E.D.

Converse

Верно и обратное: если сумма расстояний от внутренней точки треугольника до сторон не зависит от местоположения точки, треугольник является равносторонним.^[3]

Приложения

Диаграмма воспламеняемости для метана

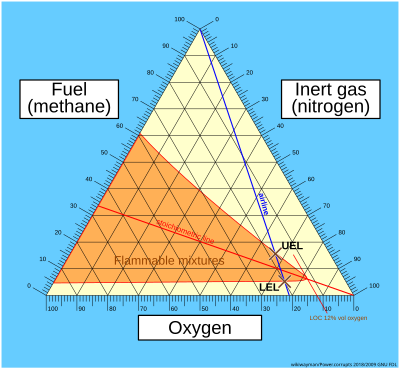
Теорема Вивиани означает, что прямые, параллельные сторонам равностороннего треугольника, дают координаты для построения тройные участки, Такие как диаграммы воспламеняемости.

В общем, они позволяют давать координаты на регулярной основе. симплекс таким же образом.

Расширения

Параллелограмм

Сумма расстояний от любой внутренней точки параллелограмм по сторонам не зависит от местоположения точки. Верно и обратное: если сумма расстояний от точки внутри четырехугольник к сторонам не зависит от расположения точки, то четырехугольник представляет собой параллелограмм.^[3]

Результат обобщается на любые 2п-угольник с параллельными противоположными сторонами. Поскольку сумма расстояний между любой парой противоположных параллельных сторон постоянна, отсюда следует, что сумма всех попарных сумм между парами параллельных сторон также постоянна. Обратное в общем случае неверно, так как результат верен для равносторонний шестиугольник, у которого не обязательно параллельны противоположные стороны.

Правильный многоугольник

Если многоугольник обычный (как равносторонние, так и равносторонний) сумма расстояний до сторон от внутренней точки не зависит от местоположения точки. В частности, он равен п раз апофема, куда п - это количество сторон, а апофема - это расстояние от центра до стороны.^[3][4] Однако обратное неверно; неквадратный параллелограмм - это контрпример.^[3]

Равноугольный многоугольник

Сумма расстояний от внутренней точки до сторон равносторонний многоугольник не зависит от расположения точки.^[1]

Выпуклый многоугольник

Необходимым и достаточным условием того, чтобы выпуклый многоугольник имел постоянную сумму расстояний от любой внутренней точки до сторон, является наличие трех неколлинеарных внутренних точек с равными суммами расстояний.^[1]

Правильный многогранник

Сумма расстояний от любой точки внутри правильный многогранник по сторонам не зависит от местоположения точки. Однако обратное неверно даже для тетраэдры.^[3]

Рекомендации

дальнейшее чтение

• Герон, Шэй; Тесслер, Ран (2002). «Проблема Ферма-Штайнера». Амер. Математика. Ежемесячно. 109 (5): 443–451. Дои:10.2307/2695644. JSTOR 2695644.
• Самельсон, Ханс (2003). «Доказательство без слов: теорема Вивиани с векторами». Математика. Mag. 76 (3): 225. Дои:10.2307/3219327. JSTOR 3219327.
• Чен, Чжибо; Лян, Тиан (2006). «Обратное к теореме Вивиани». Математический журнал колледжа. 37 (5): 390–391.
• Кавасаки, Кен-Ичиро; Яги, Йошихиро; Янагава, Кацуя (2005). «О теореме Вивиани в трех измерениях». Математика. Газ. 89 (515): 283–287. JSTOR 3621243.
• Чжоу, Ли (2012). «Многогранники Вивиани и точки Ферма». Coll. Математика. J. 43 (4): 309–312. arXiv:1008.1236. CiteSeerX 10.1.1.740.7670. Дои:10.4169 / College.math.j.43.4.309.

внешняя ссылка

• Вайсштейн, Эрик В. «Теорема Вивиани». MathWorld.
• Ли Чжоу, Многогранники Вивиани и точки Ферма
• "Теорема Вивиани: что это?". в Разрежьте узел.
• Варендорф, Джей. «Теорема Вивиани». то Вольфрам Демонстрационный проект.
• «Вариант теоремы Вивиани и некоторые обобщения». в Эскизы динамической геометрии, интерактивный эскиз динамической геометрии.
• Аббуд, Элиас (2017). «Локусы точек, вдохновленные теоремой Вивиани». arXiv:1701.07339 [math.HO].
• Армстронг, Адди; Маккуиллан, Дэн (2017). «Специализация, обобщение и новое доказательство теоремы Вивиани». arXiv:1701.01344 [math.HO].