WikiDer > Разложение вейвлет-пакета

Wavelet packet decomposition

Первоначально известный как Оптимальная структура дерева поддиапазонов (SB-TS) также называется Разложение вейвлет-пакетов (WPD) (иногда называют просто Вейвлет-пакеты или же Дерево поддиапазонов) это вейвлет преобразование, где дискретный (дискретизированный) сигнал проходит через большее количество фильтров, чем дискретное вейвлет-преобразование (DWT).

Вступление

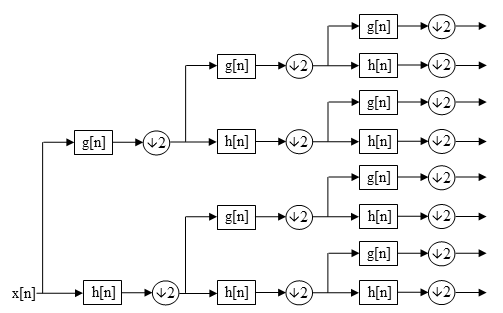
В DWT каждый уровень вычисляется путем передачи только коэффициентов предыдущего вейвлет-приближения (cAj) через дискретное время низких и высоких частот квадратурные зеркальные фильтры.[1] Однако в WPD как деталь (cDj (в одномерном случае), cHj, резюмеj, CDj (в двумерном случае)) и коэффициенты аппроксимации разлагаются для создания полного двоичного дерева.[2][3][4][5][6][7]

Разложение вейвлет-пакета на 3 уровня g [n] - это коэффициенты приближения нижних частот, h [n] - коэффициенты детализации верхних частот.

Для n уровней декомпозиции WPD дает 2п различные наборы коэффициентов (или узлов) в отличие от (n + 1) наборов для DWT. Однако из-за понижающая дискретизация процесс общее количество коэффициентов остается прежним и нет избыточности.

С точки зрения сжатия стандартное вейвлет-преобразование может не дать наилучшего результата, так как оно ограничено базовыми вейвлетами, которые увеличиваются в два раза по направлению к низким частотам. Возможно, другая комбинация оснований дает более желаемое представление для конкретного сигнала. Лучший базовый алгоритм Койфмана и Викерхаузера[1] находит набор баз, которые обеспечивают наиболее желаемое представление данных относительно конкретной функции стоимости (например, энтропия).

Были проведены соответствующие исследования в области обработки сигналов и связи для решения вопроса выбора деревьев поддиапазонов (ортогональный базис) различных видов, например регулярный, диадический, нерегулярный, по отношению к интересующим показателям производительности, включая уплотнение энергии (энтропия), корреляции поддиапазонов и другие.[3][4][5][6][7]

Теория дискретного вейвлет-преобразования (непрерывного по переменной (-ым)) предлагает приближение для преобразования дискретных (дискретизированных) сигналов. Напротив, теория дискретного преобразования поддиапазона обеспечивает идеальное представление дискретных сигналов.[5]

Галерея

  • Daubechies12-packet-functions.png
  • Добеши12-пакет-спектр.png

Приложения

Вейвлет-пакеты успешно применялись в доклинической диагностике.[8]

Рекомендации

  1. ^ а б Койфман Р.Р. и Викерхаузер М.В., 1992. Алгоритмы на основе энтропии для выбора наилучшего базиса, IEEE Transactions по теории информации, 38 (2).
  2. ^ Добеши И. (1992), Десять лекций по вейвлетам, SIAM
  3. ^ а б А.Н. Акансу и Ю. Лю, О методах разложения сигналов(Приглашенная статья), Журнал оптической инженерии, специальный выпуск Visual Communications and Image Processing, том 30, стр. 912-920, июль 1991 г.
  4. ^ а б Х. Каглар, Ю. Лю, А.Н. Акансу, Статистически оптимизированный дизайн PR-QMF, Proc. SPIE Визуальные коммуникации и обработка изображений, т. 1605, стр. 86-94, 1991.
  5. ^ а б c А.Н. Акансу и Р.А. Хаддад, Разложение сигнала с разным разрешением: преобразования, поддиапазоны и вейвлеты.Бостон, Массачусетс: Academic Press, ISBN 978-0-12-047141-6, 1992.
  6. ^ а б А. Бениассин, А. Акансу, Анализ производительности и оптимальное структурирование подканалов для дискретных многотональных трансиверов , Proc. IEEE Proc. Международный симпозиум IEEE по схемам и системам (ISCAS), стр. 1456-1459, апрель 1995 г.
  7. ^ а б М.В. Тазебай, А. Акансу, Адаптивные поддиапазонные преобразования в частотно-временных эксцизерах для систем связи DSSS, IEEE Trans. Сигнальный процесс., Т. 43, pp. 2776-2782, ноябрь 1995 г.
  8. ^ Zhang, Y .; Донг, З. (2015). «Доклиническая диагностика магнитно-резонансных (МР) изображений головного мозга с помощью дискретного вейвлет-пакетного преобразования с энтропией Цаллиса и машиной с обобщенным проксимальным опорным вектором собственных значений (GEPSVM)». Энтропия. 17 (4): 1795–1813. Bibcode:2015 Энтрп..17.1795Z. Дои:10.3390 / e17041795.

внешняя ссылка

  • Реализацию разложения вейвлет-пакетов можно найти в наборе инструментов MATLAB вейвлет: [1].
  • Реализацию R можно найти в пакете wavethresh: [2].
  • Иллюстрацию и реализацию вейвлет-пакетов вместе с их кодом на C ++ можно найти по адресу [3].
  • JWave: Реализация на Java для 1-D и 2-D вейвлет-пакетов с использованием Хаар, Добеши, Coiflet, и Legendre вейвлеты.