WikiDer > Зонтик Whitney

Сечение поверхности

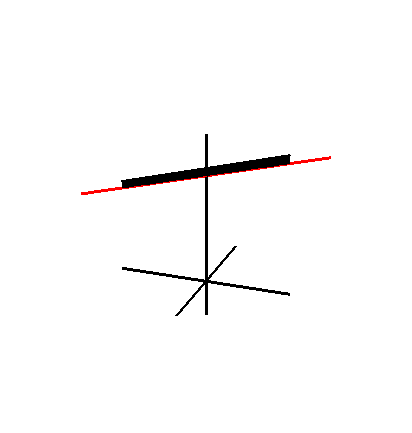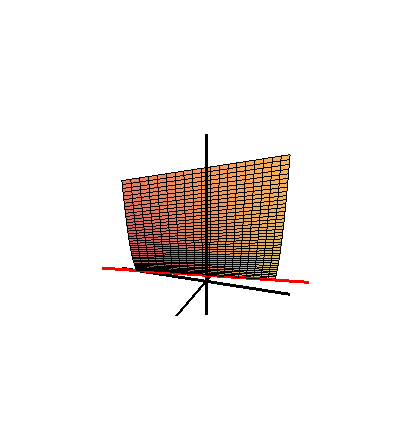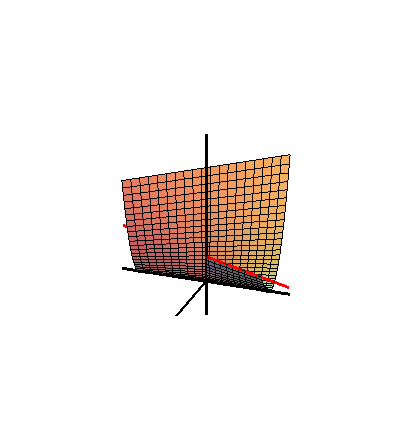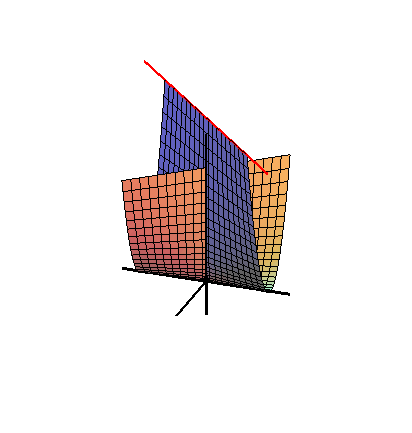
В математика, то Зонтик Whitney (или же Зонтик Уитни, названный в честь американского математика Хасслер Уитни, иногда называемый Cayley зонт) - специфическая самопересекающаяся поверхность помещен в три измерения. Это объединение всех прямых, которые проходят через точки фиксированного парабола и перпендикулярны фиксированной прямой, параллельной оси параболы и лежащей на ней перпендикулярная биссектриса.

Формулы

Зонт Уитни можно подарить параметрические уравнения в Декартовы координаты

${ Displaystyle left {{ begin {выровнено} x (u, v) & = uv, y (u, v) & = u, z (u, v) & = v ^ {2} , end {align}} right.}$

где параметры ты и v диапазон по действительные числа. Это также дается неявное уравнение

${ displaystyle x ^ {2} -y ^ {2} z = 0.}$

Эта формула также включает отрицательные z ось (которая называется ручка зонта).

Характеристики

Зонт Уитни в виде линейчатой ​​поверхности, образованной движущейся прямой линией

Зонт Уитни, сделанный из одной нитки внутри пластикового куба

Зонт Уитни - это линейчатая поверхность и правый коноид. Это важно в области теория сингулярности, как простой местный модель защемления необычность. Точка защемления и складчатая особенность единственные устойчивые локальные особенности карт из р² к р³.

Он назван в честь Американец математик Хасслер Уитни.

В теория струн, а Уитни Брейн является D7-браной, обертывающей многообразие, особенности которого локально моделируются зонтиком Уитни. Браны Уитни появляются естественным образом, если принять предел слабой связи Сена F-теория.

Смотрите также

• Перекрестная крышка
• Правый коноид
• Линейчатая поверхность

Рекомендации

• "Зонтик Уитни". Топологический зоопарк. Центр геометрии. Получено 2006-03-08. Cite имеет пустой неизвестный параметр: | accessyear = (помощь) (Изображения и видео с зонтом Уитни.)