WikiDer > Теория лезвийных элементов
Теория лезвийных элементов (ДЕРЖАТЬ ПАРИ) - математический процесс, первоначально разработанный Уильям Фроуд (1878), Дэвид В. Тейлор (1893) и Стефан Джевецки определить поведение пропеллеры. Он включает в себя разбиение лезвия на несколько мелких частей и определение сил, действующих на каждый из этих небольших элементов лезвия. Затем эти силы интегрируются вдоль всей лопасти и за один оборот ротора, чтобы получить силы и моменты, создаваемые всем гребным винтом или ротором. Одна из основных трудностей заключается в моделировании наведенной скорости на диске ротора. Из-за этого теория лопаточных элементов часто сочетается с теорией импульса для получения дополнительных соотношений, необходимых для описания наведенной скорости на диске ротора (более подробную информацию см. Теория импульса элемента клинка). На самом базовом уровне приближения предполагается однородная наведенная скорость на диске:
В качестве альтернативы изменение индуцированной скорости по радиусу можно смоделировать, разбивая лопасть на небольшие кольца и применяя сохранение массы, количества движения и энергии к каждому кольцу. Такой подход иногда называют Froude-Finsterwalder уравнение.
Если метод лопастных элементов применяется к несущим винтам вертолетов в прямом полете, необходимо учитывать колебательное движение лопастей, а также продольное и поперечное распределение наведенной скорости на диске винта. Самыми простыми моделями прямого полета являются модели первой гармоники.
Теория простого лезвия и элемента
В то время как теория импульса полезен для определения идеального КПД, он дает очень неполный отчет о работе гребных винтов, среди прочего пренебрегая крутящим моментом. Для более подробного изучения действия воздушного винта лопасти рассматриваются как состоящие из ряда небольших элементов, и рассчитываются воздушные силы, действующие на каждый элемент. Таким образом, в то время как теория импульса имеет дело с потоком воздуха, теория лопаточных элементов имеет дело прежде всего с силами, действующими на лопасти воздушного винта. Идея анализа сил на элементарных лентах лопастей гребного винта была впервые опубликована Уильямом Фроудом в 1878 году.[1] Он также был независимо разработан Джевецким и изложен в книге о механическом полете, опубликованной в России семь лет спустя, в 1885 году.[2] Опять же, в 1907 г. Lanchester опубликовал несколько более продвинутую форму теории лопастных элементов, не зная о предыдущих работах по этому вопросу. Однако простую теорию лопастных элементов обычно называют теорией Джевецкого, поскольку именно Джевецки воплотил ее в практической форме и ввел в широкое употребление. Кроме того, он был первым, кто суммировал силы на элементах лопасти, чтобы получить тягу и крутящий момент для всего воздушного винта, и первым представил идею использования данных аэродинамического профиля для определения сил, действующих на элементы лопасти.
В теории лопастных элементов Джевецкого винт считается искривленным или искривленным. профиль, каждый сегмент которого следует по винтовой траектории и рассматривается как сегмент обычного крыла. В простой теории обычно предполагается, что коэффициенты аэродинамического профиля, полученные в результате испытаний в аэродинамической трубе модельных крыльев (обычно испытываемых с удлинением 6), применяются непосредственно к элементам лопастей воздушного винта той же формы поперечного сечения.[3]
Воздушный поток вокруг каждого элемента считается двумерным, поэтому на него не влияют соседние части лопасти. Теоретически установлена независимость лопастных элементов любого заданного радиуса относительно соседних элементов.[4] и также было показано, что это в значительной степени справедливо для рабочих частей лопасти специальными экспериментами.[5] сделано для этой цели. Также предполагается, что воздух проходит через винт без радиального потока (т.е. нет сжатия потока при прохождении через диск гребного винта) и что нет столкновения лопастей.
Аэродинамические силы на элементе лопасти
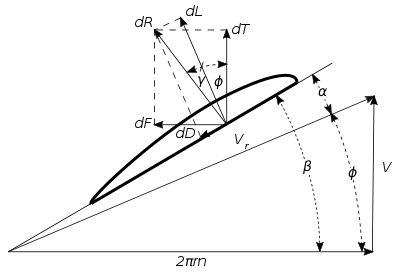
Рассмотрим элемент в радиус р, изображенный на рис.1, который имеет бесконечно малую длину доктор и ширина б. Движение элемента воздушного винта в полете происходит по винтовой траектории, определяемой поступательной скоростью. V летательного аппарата и тангенциальной скорости 2πrn элемента в плоскости винта, где п представляет количество оборотов в единицу времени. Скорость элемента относительно воздуха Vr является равнодействующей прямой и тангенциальной скоростей, как показано на рис. 2. Назовем угол между направлением движения элемента и плоскостью вращения Φ, и угол лезвия β. Тогда угол атаки элемента α относительно воздуха равен .
Применяя обычные коэффициенты аэродинамического профиля, подъемная сила на элементе равна:
Позволять γ быть углом между составляющей подъемной силы и равнодействующей силой, или . Тогда общая результирующая воздушная сила на элементе равна:
Тяга элемента - это составляющая равнодействующей силы в направлении оси воздушного винта (рис. 2), или
и с тех пор
Для удобства пусть
и
потом
а общая тяга гребного винта (лопастей B) составляет:
Снова обращаясь к Фиг.2, тангенциальная сила или сила крутящего момента равна
а крутящий момент на элементе равен
который, если , можно написать
Таким образом, выражение для крутящего момента всего гребного винта имеет вид
Мощность, потребляемая винтом, или крутящий момент в лошадиных силах, равна
а эффективность
Эффективность элемента
Из-за изменения ширины лопасти, угла и сечения аэродинамического профиля вдоль лопасти невозможно получить простое выражение для тяги, крутящего момента и эффективности гребных винтов в целом. Одиночный элемент на расстоянии около двух третей или трех четвертей радиуса наконечника, тем не менее, является достаточно репрезентативным для всего воздушного винта, и поэтому интересно исследовать выражение для эффективности отдельного элемента. Эффективность элемента - это отношение полезной мощности к потребляемой мощности, или
Сейчас же загар Φ - отношение прямой скорости к тангенциальной, а загар . Следовательно, согласно простой теории лопастных элементов, эффективность элемента гребного винта зависит только от отношения поступательной скорости к тангенциальной и от профиля профиля.
Значение Φ что дает максимальный КПД для элемента, определяемый дифференцированием КПД по отношению к Φ и приравнивая результат к нулю,
Изменение КПД с 0 показано на рис.3 для двух крайних значений γ. КПД достигает максимума при а затем снова падает до нуля при . С
ан 28,6 максимально возможный КПД элемента согласно простой теории составляет 0,932, а при из 9,5 это всего 0,812. При значениях Φ при котором работают наиболее важные элементы большинства гребных винтов (от 10 ° до 15 °), эффект по КПД еще больше. В диапазоне от 10 ° до 15 ° кривые на рис. 3 показывают, что выгодно иметь как профилей профиля и угла Φ (или продвижение на оборот, и, следовательно, шаг) как можно выше.
Ограничения теории простого лезвия
Согласно теории количества движения воздуху, проходящему через винт, передается скорость, и половина этой скорости передается воздуху к тому времени, когда он достигает плоскости пропеллера. Это увеличение скорости воздуха, проходящего в диск гребного винта, называется скоростью притока. Он всегда обнаруживается там, где есть скачок давления в жидкости. В случае горизонтального движения крыла воздуху придается нисходящая скорость, как показано на рис. 4., и теоретически половина этой скорости передается перед крылом и над ним, а другая половина - под ним и сзади.
Этот индуцированный нисходящий поток присутствует в модельных испытаниях крыла, из которых получены коэффициенты аэродинамического профиля, используемые в теории лопастных элементов; приток, указанный в теории импульса, поэтому автоматически учитывается в простой теории лопаточных элементов. Однако индуцированный нисходящий поток сильно различается для разных соотношений сторон, равняется нулю для бесконечного соотношения сторон. Большинство испытаний модели аэродинамического профиля проводится с прямоугольными крыльями, имеющими произвольно выбранное удлинение 6, и нет никаких оснований предполагать, что нисходящий поток в таком испытании соответствует притоку для каждого элемента лопасти воздушного винта. Фактически, общий вывод, сделанный из исчерпывающей серии тестов,[6] в котором распределение давления было измерено по 12 секциям модельного воздушного винта, работающего в аэродинамической трубе, заключается в том, что коэффициент подъемной силы элемента лопасти воздушного винта значительно отличается от измеренного при том же угле атаки на аэродинамическом профиле с соотношением сторон 6. Это - одна из самых слабых сторон простой теории лопаточных элементов.
Еще одним недостатком является то, что не учитывается взаимное влияние лопастей винта. Элементы лопастей на любом конкретном радиусе образуют каскад, похожий на многоплоскость с отрицательным смещением, как показано на рис. 4. Вблизи вершин, где зазор велик, натяг очень мал, но по направлению к основанию лопастей он довольно большой. большой.
В реальных гребных винтах наблюдается потеря наконечника, которую теория лопастных элементов не принимает во внимание. Таким образом, силы тяги и крутящего момента, рассчитанные с помощью теории, больше для элементов около наконечника, чем те, которые были обнаружены экспериментально.[7]
Чтобы исключить эффект масштаба, аэродинамическая труба испытания на модельных крыльях следует проводить при том же значении Число Рейнольдса (шкала) как соответствующие элементы в лопастях гребного винта. Характеристики профиля, измеренные в таком малом масштабе, как, например, скорость воздуха 30 м / ч. с 3-дюйм. хордовый профиль, демонстрируют особенности, не обнаруженные при проведении испытаний в масштабе, сопоставимом с масштабом винтовых элементов. Характеристики стандартной гребной секции, представленные на рис. 11, 12, 13 и 14 были получены из тестов с высокими числами Рейнольдса в Туннель переменной плотности N.A.C.A., и, к счастью, за исключением самого толстого из этих участков, разница в характеристиках при высоких и малых числах Рейнольдса очень мала. Эти значения могут быть использованы с разумной точностью для шкалы гребных винтов, работающих на конечных скоростях, значительно ниже скорости звука в воздухе и, следовательно, относительно свободных от каких-либо эффектов сжимаемости.
Низкая точность простой теории лопаточного элемента очень хорошо показана в отчете Дюран и Лесли,[8] в котором они вычислили характеристики большого количества модельных гребных винтов (80) и сравнили вычисленные значения с фактическими характеристиками, полученными в результате испытаний самих модельных гребных винтов. По словам авторов:
Расхождения между двумя наборами результатов, хотя и демонстрируют определенные элементы согласованности, в целом слишком велики и слишком капризно распределены, чтобы оправдать использование теории в этой простейшей форме для иных, чем приблизительные оценки, или для сравнительных целей.
Профили были испытаны в двух разных аэродинамических трубах и в одной из них при двух разных скоростях воздуха, и характеристики воздушного винта, рассчитанные на основе трех наборов данных о профиле, различаются на целых 28%, что довольно убедительно демонстрирует необходимость наличия профиля. тесты сделаны в правильном масштабе.
Несмотря на все свои неточности, простая теория лопастей и элементов оказалась полезным инструментом в руках опытных конструкторов гребных винтов. С его помощью опытный конструктор, обладающий знаниями подходящих эмпирических факторов, может спроектировать гребные винты, которые обычно достаточно хорошо соответствуют основным условиям, предъявляемым к ним, поскольку они поглощают мощность двигателя почти с надлежащей частотой вращения. Однако они не обязательно являются наиболее эффективными гребными винтами для своей цели, поскольку простая теория недостаточно точна, чтобы показать небольшие различия в эффективности из-за изменений в распределении шага, формы плана и т. Д.
Пример анализа с помощью теории простого лезвия
При выборе винта для анализа желательно знать его аэродинамические характеристики, чтобы можно было проверить точность результатов расчетов. Также желательно, чтобы анализ выполнялся для гребного винта, работающего на относительно низкой скорости на конце, чтобы не было никаких эффектов сжимаемости и чтобы он работал без помех от тела. Единственные испытания гребных винтов, которые удовлетворяют всем этим условиям, - это испытания моделей гребных винтов в аэродинамической трубе. Поэтому мы возьмем для нашего примера центральный или главный гребной винт из серии деревянных гребных винтов стандартной формы ВМС, испытанных доктором В. Ф. Дюраном в Стэнфордский университетгород.[9] Это двухлопастной винт диаметром 3 фута с равномерным геометрическим шагом 2,1 фута (или отношением диаметров шага 0,7). Лопасти имеют стандартные гребные секции на основе профиля РАФ-6 (рис. 6), а ширина, толщина и углы лопастей указаны в первой части таблицы I. В нашем анализе мы будем рассматривать винт как продвигающийся с скорость 40 миль в час и вращение со скоростью 1800 об / мин.
Для сечения 75% радиуса наконечника радиус составляет 1,125 фута, ширина лопасти составляет 0,198 фута, отношение толщины составляет 0,107, нижний изгиб равен нулю, а угол лопасти β составляет 16,6 °.
Скорость движения вперед V = 40 миль в час.
и
Угол пути
Таким образом, угол атаки
Из Рис.7, для плоского профиля с коэффициентом толщины 0,107 при угле атаки 1,1 °, γ = 3,0 °, а из рис.9 CL = 0,425. (Для участков с меньшим развалом CL следует скорректировать в соответствии с соотношением, приведенным на рис. 8, и γ дается то же значение, что и для секции с плоской поверхностью, имеющей только верхний изгиб.)
потом
и,
Также,
Расчеты Тc и Qc для шести репрезентативных элементов гребного винта даны в удобной табличной форме в Таблице I, а значения Тc и Qc показаны в зависимости от радиуса на рис. 9. Кривые, проведенные через эти точки, иногда называют кривыми градации крутящего момента. Площади под кривой представляют
и
это выражения для общей тяги и крутящего момента на лопасть на единицу динамического давления, обусловленного скоростью продвижения. Площади могут быть найдены с помощью планиметра, должное внимание, конечно, должно быть уделено шкалам значений, или интегрирование может быть выполнено приблизительно (но с удовлетворительной точностью) с помощью Правило Симпсона.
При использовании правила Симпсона радиус делится на четное число равных частей, например, десять. Затем ординату каждого деления можно найти по кривой оценки. Если исходные элементы лопасти делят лопасть на четное число равных частей, нет необходимости строить кривые классификации, но эти кривые имеют преимущество в том, что они графически показывают распределение тяги и крутящего момента вдоль лопатки. Они также обеспечивают проверку расчетов, поскольку неправильные точки обычно не образуют четкую кривую.
| D = 3,0 фута. p = 2,1 фута. | Скорость движения вперед = 40 м / ч. = 58,65 фут. / Сек. Скорость вращения = 1800 об / мин. = 30 р. С. | |||||
|---|---|---|---|---|---|---|
| r / R | 0.15 | 0.30 | 0.45 | 0.60 | 0.75 | 0.90 |
| г (футы) | 0.225 | 0.450 | 0.675 | 0.900 | 1.125 | 1.350 |
| b (футы) | 0.225 | 0.236 | 0.250 | 0.236 | 0.198 | 0.135 |
| часv/ b | 0.190 | 0.200 | 0.167 | 0.133 | 0.107 | 0.090 |
| часл/ b | 0.180 | 0.058 | 0.007 | 000 | 000 | 000 |
| β (град.) | 56.1 | 36.6 | 26.4 | 20.4 | 16.6 | 13.9 |
| 2πrn | 42.3 | 84.7 | 127.1 | 169.6 | 212.0 | 254.0 |
| 1.389 | 0.693 | 0.461 | 0.346 | 0.277 | 0.231 | |
| Φ (град.) | 54.2 | 34.7 | 24.7 | 19.1 | 15.5 | 13.0 |
| 1.9 | 1.9 | 1.7 | 1.3 | 1.1 | 0.9 | |
| γ (град.) | 3.9 | 4.1 | 3.6 | 3.3 | 3.0 | 3.0 |
| cosγ | 0.998 | 0.997 | 0.998 | 0.998 | 0.999 | 0.999 |
| CL | 0.084 | 0.445 | 0.588 | 0.514 | 0.425 | 0.356 |
| грех Φ | 0.8111 | 0.5693 | 0.4179 | 0.3272 | 0.2672 | 0.2250 |
| 0.0288 | 0.325 | 0.843 | 1.135 | 1.180 | 0.949 | |
| Φ + γ (град.) | 58.1 | 38.8 | 28.3 | 22.4 | 18.5 | 16.0 |
| соз (γ + Φ) | 0.5280 | 0.7793 | 0.8805 | 0.9245 | 0.9483 | 0.9613 |
| 0.0152 | 0.253 | 0.742 | 1.050 | 1.119 | 0.912 | |
| грех (γ + Φ) | 0.8490 | 0.6266 | 0.4741 | 0.3811 | 0.3173 | 0.2756 |
| 0.0055 | 0.0916 | 0.270 | 0.389 | 0.421 | 0.353 | |
Если обозначить абсциссы через р и ординаты в различных делениях по у1 у2 , ... y11, согласно правилу Симпсона площадь с десятью равными частями будет
Следовательно, площадь под кривой градиента тяги в нашем примере равна
и подобным образом
Вышеупомянутые интеграции также были выполнены с помощью планиметра, и средние результаты пяти испытаний согласуются с результатами, полученными с помощью правила Симпсона, в пределах одной четверти одного процента.
Тяга воздушного винта в стандартном воздухе составляет
и крутящий момент
Мощность, потребляемая гребным винтом, равна
или же
а эффективность
Рассчитанные выше характеристики сравниваются с измеренными в аэродинамической трубе следующим образом:
| Рассчитано | Модельный тест | |
|---|---|---|
| Потребляемая мощность, л.с. | 0.953 | 1.073 |
| Тяга, фунты | 7.42 | 7.77 |
| Эффективность | 0.830 | 0.771 |
Мощность, рассчитанная по простой теории лопаточных элементов, в этом случае более чем на 11% меньше, тяга составляет около 5%, а КПД составляет около 8%. Конечно, иначе рассчитанные характеристики были бы получены, если бы характеристики гребной секции из испытаний на одной и той же серии аэродинамических поверхностей в другой аэродинамической трубе были использованы, но испытания в туннелях с переменной плотностью, вероятно, являются наиболее надежными из всех.
Некоторый свет можно пролить на расхождение между расчетными и наблюдаемыми характеристиками, если снова обратиться к испытаниям распределения давления на модельном гребном винте.[6] В этих испытаниях было измерено распределение давления по нескольким секциям лопасти воздушного винта во время работы воздушного винта в аэродинамической трубе, и были выполнены три следующих серии испытаний на соответствующих аэродинамических профилях:
- а. Стандартные силовые испытания профилей с удлинением 6.
- б.Испытания распределения давления по среднему сечению указанных профилей удлинения 6.
- c. Испытания распределения давления по специальному профилю, выполненному в виде одной лопасти воздушного винта, но без закрутки, причем давление измеряется на тех же участках, что и в лопасти воздушного винта.
Результаты этих трех серий испытаний аэродинамического профиля показаны для сечения на трех четвертях радиуса законцовки на рис. 10, взятом из отчета. Следует отметить, что коэффициенты равнодействующей силы Cр довольно хорошо согласуются для среднего сечения аэродинамического профиля с удлинением 6 и соответствующего сечения специального аэродинамического профиля лопасти воздушного винта, но результирующий коэффициент силы для всего аэродинамического профиля с удлинением 6 значительно ниже. Поэтому естественно, что расчетная тяга и мощность воздушного винта должны быть слишком низкими, если основываться на характеристиках профиля для удлинения 6.
Модификации теории лезвия-элемента
Было предложено множество модификаций простой теории лопаточного элемента, чтобы сделать ее более полной и повысить ее точность. В большинстве этих модифицированных теорий делается попытка учесть столкновение лопастей, а в некоторых из них также предпринимаются попытки устранить неточность из-за использования данных аэродинамического профиля из испытаний на крыльях, имеющих конечное удлинение, например 6. Первая модификация, которая была сделана, заключалась в сочетании простой теории Джевецкого с теорией импульса Фруда.
Диаграммы
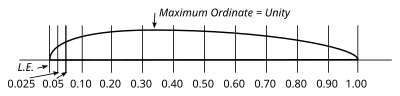
- Стандартные винтовые секции на основе R.A.F.-6 Infinite.
Атрибуция
![]() В эту статью включен текст из публикации, которая сейчас находится в всеобщее достояние: Вейк, Фред Эрнест (1899). Конструкция воздушного винта. Нью-Йорк, McGraw-Hill Book Company, inc.
В эту статью включен текст из публикации, которая сейчас находится в всеобщее достояние: Вейк, Фред Эрнест (1899). Конструкция воздушного винта. Нью-Йорк, McGraw-Hill Book Company, inc.
Смотрите также
внешняя ссылка
- Анализ элементов лопастей для гребных винтов
- Теория вертолета - Теория лопастных элементов в прямом полете из Aerospaceweb.org
- Теория лезвийных элементов
- Стефан Джевецки 1903
- QBlade: программное обеспечение с открытым исходным кодом Blade Element Method от H.F.I. TU Berlin
- NASA-TM-102219: Обзор моделей неоднородного притока для динамики полета винтокрылых аппаратов и приложений управления, Роберт Чен, НАСА
Рекомендации
- ^ Фруд, Уильям (1878). Элементарная связь между тангажем, скольжением и тяговым усилием. Inst. Военно-морские архитекторы.
- ^ На этот факт, о котором мало кто знает в англоязычных странах, обратил внимание автора профессор Ф. В. Павловски из Мичиганского университета. Первая французская статья Джевецкого по его теории была опубликована в 1892 году. Он написал во всех семи статьях о силовых установках самолетов, которые были представлены Академии наук, Морской ассоциации техники и Le Congrès International d'Architecture et de Construction Navale. 15 июля 1900 г. Он, наконец, написал книгу, обобщающую все его работы, под названием «Генеральная теория движущей силы», изданная в 1920 г. Готье-Виллар в Париже.
- ^ Джевецки предположил, что характеристики крылового профиля могут быть получены при испытаниях винтов на специальных моделях.
- ^ Глауэрт, H (1926). Теория Aerofoil и Airscrew. Издательство Кембриджского университета.
- ^ К. Н. Х., Лок; Bateman, H .; Тауненд, Х. К. Х. (1924). Эксперименты по проверке независимости элементов лопасти винта. Британский Р. и М. 953.
- ^ а б Fage, A .; Ховард, Р. Г. (1921). Рассмотрение теории винта в свете данных, полученных в результате экспериментального исследования распределения давления по всей поверхности лопасти винта, а также по профилям соответствующей формы. Британский Р. и М. 681.
- ^ К. Н. Х. Лок и Х. Бейтман, Британский Р. и М. 892, 1923, «Анализ семейства воздушных винтов с помощью теории вихрей и измерения полного напора».
- ^ Сравнение испытаний модели воздушного винта с теорией аэродинамического профиля, Уильям Ф. Дюран и Э. П. Лесли, N.A.C.A.T.R. 196, 1924 г.
- ^ Дюран, В. Ф. (1926). Испытания тринадцати гребных винтов типа ВМФ. N.A.C.A .T.R. 237. Пропеллер модели C.
















































![{ displaystyle int _ {0} ^ {R} F (r) dr = { frac { bigtriangleup r} {3}} [y_ {1} +2 (y_ {3} + y_ {5} + y_ {7} + y_ {9}) + 4 (y_ {2} + y_ {4} + y_ {6} + y_ {8} + y_ {10}) + y_ {11}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e09aa182193ed3623bdacb66ba7fe1cce7f760a)
![{ displaystyle { begin {align} int _ {0} ^ {R} T_ {c} dr & = { frac {0,15} {3}} [0 + 2 (0,038 + 0,600 + 1,050 + 1,091) +4 (0 + 0,253 + 0,863 + 1,120 + 0912) +0] & = 0,9075, конец {выровнен}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b75f87189c9c41460c0d07104579c8dfedd9d92)










