WikiDer > Каноническая форма

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Каноническая форма» – Новости · газеты · книги · ученый · JSTOR (Декабрь 2007 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Алгоритмический анаграмма тест с использованием мультимножества как канонические формы: струны "мадам Кюри" и "радий пришел"даны как C массивы. Каждый преобразуется в каноническую форму путем сортировки. Поскольку обе отсортированные строки буквально совпадают, исходные строки были анаграммами друг друга.

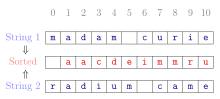
В математика и Информатика, а канонический, нормальный, или же стандарт форма из математический объект это стандартный способ представления этого объекта как математическое выражение. Часто это тот, который обеспечивает простейшее представление объекта и позволяет его уникальным образом идентифицировать.^[1] Различие между «канонической» и «нормальной» формами варьируется от подполя к подполю. В большинстве полей каноническая форма определяет уникальный представление для каждого объекта, в то время как нормальная форма просто определяет его форму без требования уникальности.^[2]

Каноническая форма положительное число в десятичное представление конечная последовательность цифр, не начинающаяся с нуля. В более общем смысле, для класса объектов, на котором отношение эквивалентности определено, каноническая форма заключается в выборе конкретного объекта в каждом классе. Например:

• Нормальная форма Джордана каноническая форма для матричное подобие.
• В форма эшелона строки является канонической формой, если рассматривать как эквивалентную матрицу и ее левое произведение на обратимая матрица.

В информатике, а точнее в компьютерная алгебра, при представлении математических объектов на компьютере обычно существует много разных способов представления одного и того же объекта. В этом контексте каноническая форма представляет собой такое представление, что каждый объект имеет уникальное представление (с канонизация являясь процессом, посредством которого представление принимает свою каноническую форму).^[3] Таким образом, равенство двух объектов легко проверить, проверив равенство их канонических форм.

Несмотря на это преимущество, канонические формы часто зависят от произвольного выбора (например, упорядочивания переменных), что создает трудности при проверке равенства двух объектов в результате независимых вычислений. Следовательно, в компьютерной алгебре нормальная форма - более слабое понятие: A нормальная форма - представление такое, что ноль представлен однозначно. Это позволяет проверять равенство, переводя разницу двух объектов в нормальную форму.

Каноническая форма также может означать дифференциальная форма который определяется естественным (каноническим) способом.

Определение

Учитывая набор S объектов с отношение эквивалентности R на S, а каноническая форма дается обозначением некоторых объектов S быть «в канонической форме», так что каждый рассматриваемый объект эквивалентен ровно одному объекту в канонической форме. Другими словами, канонические формы в S представляют классы эквивалентности один раз и только один раз. Чтобы проверить, эквивалентны ли два объекта, достаточно проверить равенство их канонических форм. Таким образом, каноническая форма обеспечивает классификационная теорема и более того, поскольку он не только классифицирует каждый класс, но также дает выделенного (канонического) представителя для каждого объекта в классе.

Формально канонизация отношения эквивалентности р на съемочной площадке S это отображение c:S→S такой, что для всех s, s₁, s₂ ∈ S:

1. c(s) = c(c(s))   (идемпотентность),
2. s₁ р s₂ если и только если c(s₁) = c(s₂) (решительность) и
3. s р c(s) (репрезентативность).

Свойство 3 избыточно; следует применить 2 к 1.

С практической точки зрения часто бывает полезно уметь распознавать канонические формы. Также необходимо подумать о практическом алгоритмическом вопросе: как перейти от данного объекта s в S в его канонической форме s*? Канонические формы обычно используются для повышения эффективности работы с классами эквивалентности. Например, в модульная арифметика, канонической формой для класса вычетов обычно считается наименьшее неотрицательное целое число в нем. Операции над классами выполняются путем объединения этих представителей, а затем уменьшения результата до его наименее неотрицательного остатка. Требование уникальности иногда ослабляется, позволяя формам быть уникальными с точностью до некоторого более тонкого отношения эквивалентности, такого как разрешение переупорядочения сроки (если нет естественной упорядоченности по срокам).

Каноническая форма может быть просто условностью или глубокой теоремой. Например, полиномы условно записываются с членами в убывающей степени: обычно пишут Икс² + Икс + 30 чем Икс + 30 + Икс², хотя две формы определяют один и тот же многочлен. Напротив, существование Иорданская каноническая форма для матрицы - глубокая теорема.

Примеры

Примечание: в этом разделе "вплоть до«некоторое отношение эквивалентности E означает, что каноническая форма в целом не уникальна, но если один объект имеет две различные канонические формы, они E-эквивалентны.

Обозначение большого числа

Стандартная форма используется многими математиками и учеными для написания чрезвычайно большие числа более кратким и понятным языком, наиболее заметным из которых является научная нотация.^[4]

Теория чисел

• Каноническое представление положительного целого числа
• Каноническая форма непрерывная дробь

Линейная алгебра

Объекты	А эквивалентно B если:	Нормальная форма	Примечания
Нормальный матрицы над сложные числа	${ displaystyle A = U ^ {*} BU}$ для некоторых унитарная матрица U	Диагональные матрицы (до повторного заказа)	Это Спектральная теорема
Матрицы над комплексными числами	${ displaystyle A = UBV ^ {*}}$ для некоторых унитарные матрицы U и V	Диагональные матрицы с действительными положительными элементами (в порядке убывания)	Разложение по сингулярным числам
Матрицы над алгебраически замкнутое поле	${ displaystyle A = P ^ {- 1} BP}$ для некоторых обратимый матрица п	Нормальная форма Джордана (вплоть до переупорядочивания блоков)
Матрицы над алгебраически замкнутое поле	${ displaystyle A = P ^ {- 1} BP}$ для некоторых обратимый матрица п	Каноническая форма Вейра (вплоть до переупорядочивания блоков)
Матрицы над полем	${ displaystyle A = P ^ {- 1} BP}$ для некоторых обратимый матрица п	Нормальная форма Фробениуса
Матрицы над главная идеальная область	${ displaystyle A = P ^ {- 1} BQ}$ для некоторых обратимый Матрицы п и Q	Нормальная форма Смита	Эквивалентность аналогична разрешению обратимых преобразований элементарных строк и столбцов.
Матрицы над целыми числами	${ displaystyle A = UB}$ для некоторых унимодулярный матрица U	Нормальная форма Эрмита
Конечномерный векторные пространства над полем K	А и B изоморфны как векторные пространства	${ displaystyle K ^ {n}}$, п неотрицательное целое число

Алгебра

Геометрия

В аналитическая геометрия:

• Уравнение линии: Топор + К = C, с А² + B² = 1 и C ≥ 0
• Уравнение круга: ${ Displaystyle (х-в) ^ {2} + (у-к) ^ {2} = г ^ {2}}$

Напротив, существуют альтернативные формы для написания уравнений. Например, уравнение линии может быть записано как линейное уравнение в точечный уклон и форма пересечения склонов.

Выпуклые многогранники можно поместить в каноническая форма такой, что:

• Все лица плоские,
• Все ребра касаются единичной сферы, и
• Центроид многогранника находится в начале координат.^[5]

Интегрируемые системы

Каждый дифференцируемый многообразие имеет котангенсный пучок. Этот набор всегда можно наделить определенным дифференциальная форма, называется каноническая одноформа. Эта форма придает котангенсному расслоению структуру симплектическое многообразие, и позволяет интегрировать векторные поля на многообразии с помощью Уравнения Эйлера-Лагранжа, или с помощью Гамильтонова механика. Такие системы интегрируемых дифференциальные уравнения называются интегрируемые системы.

Динамические системы

Изучение динамические системы перекрывается с интегрируемые системы; там есть идея нормальная форма (динамические системы).

Трехмерная геометрия

При изучении многообразий в трех измерениях каждый имеет первая фундаментальная форма, то вторая основная форма и третья основная форма.

Функциональный анализ

Объекты	А эквивалентно B если:	Нормальная форма
Гильбертовы пространства	Если А и B оба являются гильбертовыми пространствами бесконечной размерности, то А и B изометрически изоморфны.	${ displaystyle ell ^ {2} (I)}$ пробелы последовательности (вплоть до замены индексного набора я с другим набором индексов того же мощность)
Коммутативный ${ displaystyle C ^ {*}}$-алгебры с единицей	А и B изоморфны как ${ displaystyle C ^ {*}}$-алгебры	Алгебра ${ Displaystyle C (X)}$ непрерывных функций на компактный Пространство Хаусдорфа, вплоть до гомеоморфизм базовой площади.

Классическая логика

• Нормальная форма отрицания
• Конъюнктивная нормальная форма
• Дизъюнктивная нормальная форма
• Алгебраическая нормальная форма
• Prenex нормальная форма
• Сколем нормальная форма
• Каноническая форма Блейка, также известная как полная сумма простых импликант, полная сумма или дизъюнктивная простая форма

Теория множеств

• Нормальная форма Кантора из порядковый номер

Теория игры

• Игра в нормальной форме

Теория доказательств

• Нормальная форма (естественная дедукция)

Системы перезаписи

Символическое преобразование формулы из одной формы в другую называется «переписыванием» этой формулы. Можно изучить абстрактные свойства переписывания общих формул, изучив набор правил, с помощью которых можно корректно манипулировать формулами. Это «правила переписывания» - неотъемлемая часть абстрактная система переписывания. Часто возникает вопрос, можно ли привести какое-то общее выражение к единой общей форме, нормальной форме. Если разные последовательности перезаписей по-прежнему приводят к одной и той же форме, то эту форму можно назвать нормальной формой, а перезапись - сливающейся. Не всегда удается получить нормальную форму.

Лямбда-исчисление

• Лямбда-член находится в бета нормальная форма если бета-редукция невозможна; лямбда-исчисление является частным случаем абстрактной системы перезаписи. В нетипизированном лямбда-исчислении, например, термин ${ Displaystyle ( лямбда х. (хх) ; лямбда х. (хх))}$ не имеет нормальной формы. В типизированном лямбда-исчислении каждый правильно сформированный термин можно переписать в его нормальную форму.

Теория графов

В теория графов, раздел математики, канонизация графа проблема нахождения канонической формы данного графа грамм. Каноническая форма - это помеченный график Canon (грамм) то есть изоморфный к грамм, такой, что любой граф, изоморфный грамм имеет ту же каноническую форму, что и грамм. Таким образом, из решения проблемы канонизации графа, можно было бы также решить проблему изоморфизм графов: проверить, есть ли два графика грамм и ЧАС изоморфны, вычислить их канонические формы Canon (грамм) и Canon (ЧАС) и проверьте, идентичны ли эти две канонические формы.

Вычисление

В вычисление, приведение данных к любой канонической форме обычно называется нормализация данных.

Например, нормализация базы данных это процесс организации поля и столы из реляционная база данных минимизировать избыточность и зависимость.^[6]

В области безопасность программного обеспечения, обычный уязвимость не отмечен злонамеренный ввод (см. Внедрение кода). Смягчение этой проблемы правильное проверка ввода. Перед выполнением проверки ввода, ввод обычно нормализуется путем исключения кодирования (например, Кодировка HTML) и сводя входные данные к одному общему набор символов.

Другие формы данных, обычно связанные с обработка сигналов (включая аудио и визуализация) или же машинное обучение, можно нормализовать, чтобы получить ограниченный диапазон значений.

Смотрите также

• Канонизация
• Каноническая основа
• Канонический класс
• Нормализация (значения)
• Стандартизация

Примечания

Рекомендации

• Шилов, Георгий Э. (1977), Сильверман, Ричард А. (ред.), Линейная алгебра, Дувр, ISBN 0-486-63518-X.
• Хансен, Ван Лундсгаард (2006), Функциональный анализ: вход в гильбертово пространство, Мировое научное издательство, ISBN 981-256-563-9.