WikiDer > Упаковка круга в равносторонний треугольник
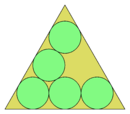
Упаковка круга в равносторонний треугольник это проблема упаковки в дискретная математика где цель состоит в том, чтобы упаковать п единичные круги в минимально возможные равносторонний треугольник. Оптимальные решения известны п <13 и для любого треугольное число кругов, и предположения доступны для п < 28.[1][2][3]
Гипотеза Пол Эрдёш и Норман Олер утверждает, что если п - треугольное число, то оптимальные упаковки п − 1 и из п окружности имеют одинаковую длину стороны: то есть, согласно гипотезе, оптимальная упаковка для п − 1 круги можно найти, удалив любой единственный круг из оптимальной гексагональной упаковки п круги.[4] Теперь известно, что эта гипотеза верна для п ≤ 15.[5]
Минимальные решения для длины стороны треугольника:[1]
| Количество кругов | Треугольный | Длина | Площадь |
|---|---|---|---|
| 1 | Истинный | = 3.464... | 5.196... |
| 2 | Ложь | = 5.464... | 12.928... |
| 3 | Истинный | = 5.464... | 12.928... |
| 4 | Ложь | = 6.928...  | 20.784... |
| 5 | Ложь | = 7.464...   | 24.124... |
| 6 | Истинный | = 7.464... | 24.124... |
| 7 | Ложь | = 8.928... | 34.516... |
| 8 | Ложь | = 9.293... | 37.401... |
| 9 | Ложь | = 9.464... | 38.784... |
| 10 | Истинный | = 9.464... | 38.784... |
| 11 | Ложь | = 10.730... | 49.854... |
| 12 | Ложь | = 10.928... | 51.712... |
| 13 | Ложь | = 11.406... | 56.338... |
| 14 | Ложь | = 11.464... | 56.908... |
| 15 | Истинный | = 11.464... | 56.908... |
Тесно связанная с этим проблема состоит в том, чтобы покрыть равносторонний треугольник фиксированным числом равных кругов, имеющих как можно меньший радиус.[6]
Смотрите также
- Упаковка круга в равнобедренный прямоугольный треугольник
- Круги Малфатти, конструкция, дающая оптимальное решение для трех окружностей в равностороннем треугольнике
Рекомендации
- ^ а б Мелиссен, Ханс (1993), "Плотные упаковки конгруэнтных кругов в равносторонний треугольник", Американский математический ежемесячник, 100 (10): 916–925, Дои:10.2307/2324212, JSTOR 2324212, МИСТЕР 1252928.
- ^ Melissen, J. B.M .; Шур, П. К. (1995), «Упаковка 16, 17 или 18 кругов в равносторонний треугольник», Дискретная математика, 145 (1–3): 333–342, Дои:10.1016 / 0012-365X (95) 90139-C, МИСТЕР 1356610.
- ^ Грэм, Р. Л.; Любачевский, Б. Д. (1995), «Плотные упаковки равных дисков в равностороннем треугольнике: от 22 до 34 и далее», Электронный журнал комбинаторики, 2: Статья 1, прим. 39 стр. (В электронном виде), МИСТЕР 1309122.
- ^ Олер, Норман (1961), "Проблема конечной упаковки", Канадский математический бюллетень, 4 (2): 153–155, Дои:10.4153 / CMB-1961-018-7, МИСТЕР 0133065.
- ^ Паян, Чарльз (1997), "Empilement de cercles égaux dans un quadquilatéral. À Propos d'une conjecture d'Erdős-Oler", Дискретная математика (на французском языке), 165/166: 555–565, Дои:10.1016 / S0012-365X (96) 00201-4, МИСТЕР 1439300.
- ^ Нурмела, Кари Дж. (2000), «Предположительно оптимальные покрытия равностороннего треугольника, содержащего до 36 равных окружностей», Экспериментальная математика, 9 (2): 241–250, Дои:10.1080/10586458.2000.10504649, МИСТЕР 1780209, S2CID 45127090.
 | Этот Связанные с элементарной геометрией статья - это заглушка. Вы можете помочь Википедии расширяя это. |