WikiDer > Cograph

В График Турана Т(13,4), пример кографа

В теория графов, а cograph, или же дополняемо-приводимый граф, или же п₄-свободный график, это график который может быть сгенерирован из одновершинного графа K₁ к дополнение и несвязный союз. То есть семейство кографов - это наименьший класс графов, который включает K₁ и замкнут относительно дополнения и дизъюнктного объединения.

Кографы были открыты независимо несколькими авторами с 1970-х годов; ранние ссылки включают Юнг (1978), Lerchs (1971), Сейнше (1974), и Самнер (1974). Их также называли D * -графы,^[1] наследственные графы Дейси (после связанной работы Джеймса К. Дейси-младшего на ортомодульные решетки),^[2] и 2-четные графы.^[3]Они имеют простую структурную декомпозицию с участием несвязный союз и дополнительный граф операции, которые могут быть кратко представлены в виде помеченного дерева и алгоритмически использоваться для эффективного решения многих проблем, таких как поиск максимальная клика которые трудны для более общих классов графов.

Частные случаи кографов включают полные графики, полные двудольные графы, кластерные графы, и графики пороговых значений. Кографы, в свою очередь, являются частными случаями дистанционно-наследственные графы, графы перестановок, графики сопоставимости, и идеальные графики.

Определение

Рекурсивная конструкция

Любой кограф может быть построен по следующим правилам:

1. любой граф с единственной вершиной является cograph;
2. если ${ displaystyle G}$ Кограф, и его дополнительный граф ${ displaystyle { overline {G}}}$;
3. если ${ displaystyle G}$ и ${ displaystyle H}$ являются кографами, поэтому их несвязный союз ${ Displaystyle G чашка H}$.

Кографы могут быть определены как графы, которые могут быть построены с использованием этих операций, начиная с графов с одной вершиной.^[4]В качестве альтернативы, вместо использования операции дополнения, можно использовать операцию соединения, которая состоит в формировании несвязного объединения ${ Displaystyle G чашка H}$ а затем добавляем ребро между каждой парой вершин из ${ displaystyle G}$ и вершина из ${ displaystyle H}$.

Другие характеристики

Можно дать несколько альтернативных характеристик кографов. Среди них:

• Кограф - это граф, не содержащий дорожка п₄ на 4 вершинах (и, следовательно, длины 3) как индуцированный подграф. То есть граф является кографом тогда и только тогда, когда для любых четырех вершин ${ displaystyle v_ {1}, v_ {2}, v_ {3}, v_ {4}}$, если ${ Displaystyle {v_ {1}, v_ {2} }, {v_ {2}, v_ {3} }}$ и ${ displaystyle {v_ {3}, v_ {4} }}$ являются ребрами графа, то хотя бы одно из ${ Displaystyle {v_ {1}, v_ {3} }, {v_ {1}, v_ {4} }}$ или же ${ displaystyle {v_ {2}, v_ {4} }}$ тоже край.^[4]
• Кограф - это граф, все индуцированные подграфы которого обладают тем свойством, что любой максимальный клика пересекает любые максимальное независимое множество в одной вершине.
• Кограф - это граф, в котором каждый нетривиальный индуцированный подграф имеет не менее двух вершин с одинаковыми окрестностями.
• Кограф - это граф, в котором каждый связный индуцированный подграф имеет несвязное дополнение.
• Кограф - это граф, все связные индуцированные подграфы имеют диаметр максимум 2.
• Кограф - это граф, в котором каждый связный компонент это дистанционно-наследственный граф диаметром не более 2.
• Кограф - это граф с ширина клики максимум 2.^[5]
• Кограф - это график сопоставимости из последовательно-параллельный частичный порядок.^[1]
• Кограф - это граф перестановок из отделимая перестановка.^[6]
• Кограф - это граф, все минимальные аккордовые окончания находятся тривиально совершенные графы.^[7]
• Кограф - это по наследству хорошо раскрашенный график, граф такой, что каждый жадная окраска каждого индуцированного подграфа использует оптимальное количество цветов.^[8]
• Граф является кографом тогда и только тогда, когда каждая вершина графа имеет порядок вершин. идеальный порядок, поскольку не имея п₄ означает, что никаких препятствий для идеального порядка не существует ни в каком порядке вершин.

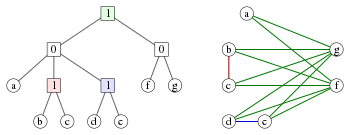
Cotrees

Дерево и соответствующий граф. Каждый край (ты,v) в кографе имеет цвет, соответствующий цвету наименее общего предка ты и v в дереве.

А Cotree это дерево, в котором внутренние узлы помечены числами 0 и 1. Каждое cotree Т определяет cograph грамм имея листья Т как вершины, и в котором поддерево укоренено в каждом узле Т соответствует индуцированный подграф в грамм определяется набором листьев, спускающихся с этого узла:

• Поддерево, состоящее из единственного листового узла, соответствует индуцированному подграфу с единственной вершиной.
• Поддерево с корнем в узле с меткой 0 соответствует объединению подграфов, определенных дочерними элементами этого узла.
• Поддерево с корнем в узле с меткой 1 соответствует присоединиться подграфов, определенных дочерними элементами этого узла; то есть мы формируем объединение и добавляем ребро между каждыми двумя вершинами, соответствующими листам в разных поддеревьях. В качестве альтернативы объединение набора графов можно рассматривать как образованное путем дополнения каждого графа, формирования объединения дополнений и последующего дополнения полученного объединения.

Эквивалентный способ описания кографа, образованного из дерева, состоит в том, что две вершины соединены ребром тогда и только тогда, когда наименьший общий предок соответствующих листьев помечены цифрой 1. И наоборот, каждый cograph может быть представлен таким образом cotree. Если мы требуем, чтобы метки на любом пути корневого листа этого дерева чередовались между 0 и 1, это представление будет уникальным.^[4]

Вычислительные свойства

Кографы могут быть распознаны в линейном времени, а представление cotree построено с использованием модульная декомпозиция,^[9] уточнение раздела,^[10] LexBFS ,^[11] или же расщепление.^[12] После того, как представление cotree построено, многие знакомые проблемы с графами могут быть решены с помощью простых вычислений снизу вверх на cotree.

Например, чтобы найти максимальная клика в cograph вычислить в восходящем порядке максимальную клику в каждом подграфе, представленном поддеревом cotree. Для узла с меткой 0 максимальная клика является максимальной среди клик, вычисленных для дочерних узлов этого узла. Для узла с меткой 1 максимальная клика представляет собой объединение клик, вычисленных для дочерних узлов этого узла, и имеет размер, равный сумме размеров дочерних клик. Таким образом, поочередно максимизируя и суммируя значения, хранящиеся в каждом узле cotree, мы можем вычислить максимальный размер клики, а поочередно максимизируя и взяв объединения, мы можем построить саму максимальную клику. Подобные вычисления дерева снизу вверх позволяют максимальный независимый набор, число раскраски вершин, максимальное покрытие клики и гамильтоничность (т. е. существование Гамильтонов цикл) для вычисления за линейное время из cotree-представления кографа.^[4] Поскольку кографы имеют ограниченную ширину клики, Теорема Курселя может использоваться для проверки любого свойства в монадическом втором порядке логика графиков (MSO₁) на кографах за линейное время.^[13]

Проблема проверки того, является ли данный граф k вершины далеко и / или т края от кографа управляемый с фиксированными параметрами.^[14] Решаем, можно ли k-Кромко-удалено к графу может быть решено за O^*(2.415^k) время,^[15] и k-Отредактировано по краю к графу в O^*(4.612^k).^[16] Если самый большой индуцированный подграф графа графа можно найти, удалив k вершин графа, его можно найти за O^*(3.30^k) время.^[15]

Два кографа изоморфный тогда и только тогда, когда их родовые деревья (в канонической форме без двух смежных вершин с одинаковой меткой) изоморфны. Из-за этой эквивалентности можно определить за линейное время, изоморфны ли два кографа, построив их дочерние деревья и применив линейный тест изоморфизма времени для помеченных деревьев.^[4]

Если ЧАС является индуцированный подграф кографа грамм, тогда ЧАС сам по себе cograph; cotree для ЧАС может быть сформирован путем удаления части листьев с дерева для грамм а затем подавление узлов, у которых есть только один дочерний элемент. Это следует из Теорема Крускала о дереве что связь быть индуцированным подграфом хорошо квазиупорядоченный на кографах.^[17] Таким образом, если подсемейство кографов (например, планарный cographs) замкнут относительно операций индуцированного подграфа, то он имеет конечное число запрещенные индуцированные подграфы. С вычислительной точки зрения это означает, что проверка принадлежности к такому подсемейству может выполняться за линейное время, используя восходящее вычисление на cotree данного графа, чтобы проверить, содержит ли он какой-либо из этих запрещенных подграфов. Однако, когда размеры двух кографов являются переменными, проверка того, является ли один из них индуцированным подграфом другого, является НП-полный.^[18]

Кографы играют ключевую роль в алгоритмах распознавания функции однократного чтения.^[19]

Перечисление

Количество подключенных кографов с п вершины, для п = 1, 2, 3, ..., это:

1, 1, 2, 5, 12, 33, 90, 261, 766, 2312, 7068, 21965, 68954, ... (последовательность A000669 в OEIS)

За п > 1 существует одинаковое количество отключенных кографов, потому что для каждого кографа ровно один или его дополнительный граф подключен.

Связанные семейства графов

Подклассы

Каждый полный график K_п является копографом, в котором cotree состоит из одного 1-узла и п листья. Точно так же каждый полный двудольный граф K_а,б это cograph. Его cotree базируется на 1-узле, у которого есть два дочерних узла с 0 узлами, один с а лист детей и один с б лист детей.A График Турана может быть сформирован путем объединения семейства независимых множеств равного размера; таким образом, это также cograph, cotree которого базируется на 1-узле, который имеет дочерний 0-узел для каждого независимого набора.

Каждый график пороговых значений тоже cograph. Пороговый граф может быть сформирован путем многократного добавления одной вершины, либо связанной со всеми предыдущими вершинами, либо ни с одной из них; каждая такая операция является одной из операций непересекающегося объединения или соединения, посредством которых может быть образовано cotree.^[20]

Суперклассы

Характеристика кографов тем свойством, что каждая клика и максимальное независимое множество имеют непустое пересечение, является более сильной версией определяющего свойства сильно совершенные графы, в котором каждый индуцированный подграф содержит независимое множество, пересекающее все максимальные клики. В кографе каждое максимальное независимое множество пересекает все максимальные клики. Таким образом, каждый кограф абсолютно совершенен.^[21]

Тот факт, что кографы п₄-free означает, что они отлично поддается заказу. Фактически, каждый порядок вершин кографа является совершенным порядком, что дополнительно подразумевает, что максимальное нахождение клики и минимальная раскраска могут быть найдены за линейное время с любой жадной раскраской и без необходимости в декомпозиции cotree.

Каждый cograph - это дистанционно-наследственный граф, что означает, что каждый индуцированный путь в кографе кратчайший путь. Кографы могут быть охарактеризованы среди дистанционно-наследственных графов как имеющие диаметр два в каждой компоненте связности. график сопоставимости из последовательно-параллельный частичный порядок, полученный заменой дизъюнктного объединения и операций соединения, с помощью которых был построен копограф, дизъюнктным объединением и порядковая сумма операций над частичными порядками, потому что сильно совершенные графы, идеально упорядочиваемые графы, графы с дистанционной наследственностью и графы сопоставимости - все это идеальные графики, Кографы тоже прекрасны.^[20]

Примечания

Рекомендации

внешняя ссылка

• «Кограф-графики», Информационная система по включению классов графов
• Вайсштейн, Эрик В. «Кограф». MathWorld.