WikiDer > Модульная декомпозиция
В теория графов, то модульная декомпозиция является разложением график на подмножества вершин, называемых модули. Модуль - это обобщение связный компонент графа. Однако, в отличие от связанных компонентов, один модуль может быть надлежащим подмножеством другого. Таким образом, модули приводят к рекурсивному (иерархическому) разбиению графа, а не просто к разбиению.
Возможны варианты модульной декомпозиции для неориентированные графы и ориентированные графы. Для каждого неориентированного графа это разложение уникально.
Это понятие может быть обобщено на другие структуры (например, ориентированные графы) и полезно для разработки эффективных алгоритмов распознавания некоторых классов графов, для поиска транзитивных ориентаций графики сопоставимости, для проблемы оптимизации на графиках, а для рисунок графика.
Модули
Поскольку понятие модулей было переоткрыто во многих областях, модули также были названы автономные комплексы, однородные множества, интервалы, и партитивные наборы. Возможно, самое раннее упоминание о них и первое описание модульных частных и разложения графов, которые они вызывают, появились в (Галлай 1967).
А модуль графа является обобщением связный компонент. Связанный компонент обладает тем свойством, что он представляет собой набор таких вершин, что каждый член это не сосед каждой вершины не в . (Это объединение компонентов связности тогда и только тогда, когда оно обладает этим свойством.) В более общем смысле, является модулем, если для каждой вершины , либо каждый член не является соседом или каждый член является соседом .
Эквивалентно, является модулем, если все члены имеют одинаковый набор соседей среди вершин, не принадлежащих .
В отличие от связных компонентов, модули графа такие же, как модули его дополнять, и модули могут быть «вложенными»: один модуль может быть правильным подмножеством другого. Обратите внимание, что набор вершин графа является модулем, как и его одноэлементные подмножества и пустое множество; это называется тривиальные модули. Граф может иметь или не иметь других модулей. Граф называется премьер если все его модули тривиальны.
Несмотря на эти различия, модули сохраняют желаемое свойство связных компонентов, а именно то, что многие свойства подграфа индуцированный связным компонентом не зависят от остальной части графа. Аналогичное явление также применимо к подграфам, индуцированным модулями.
Поэтому модули графа представляют большой алгоритмический интерес. Набор вложенных модулей, примером которых является модульная декомпозиция, можно использовать для рекурсивного решения многих комбинаторных задач на графах, таких как распознавание и транзитивное ориентирование. графики сопоставимости, распознавая и находя перестановочные представления графы перестановок, распознавая, является ли граф cograph и найдя справку об ответе на вопрос, узнав интервальные графики и находим для них интервальные представления, определяя дистанционно-наследственные графы (Spinrad, 2003) и для рисунок графика (Пападопулос, 2006). Они играют важную роль в знаменитом доказательстве того, что Ловас теорема о совершенном графе (Голумбик, 1980).
Для распознавания дистанционно-наследственных графов и круговые графики, дальнейшее обобщение модульной декомпозиции, названное расщепление, особенно полезен (Spinrad, 2003).
Чтобы избежать двусмысленности в приведенных выше определениях, мы дадим следующие формальные определения модулей. . это модуль из если:
- вершины нельзя выделить ни одной вершиной в , т.е. , либо примыкает к обоим и или не примыкает к ни к .
- вершины имеют одинаковый набор внешних соседей, т.е. .
, и все синглтоны для являются модулями и называются тривиальные модули. График премьер если все его модули тривиальны. Подключенные компоненты графа , или его дополнительного графа также являются модулями .
это сильный модуль графа если он не перекрывает любой другой модуль : модуль , либо или или .
Модульные коэффициенты и коэффициенты
Если и являются непересекающимися модулями, то легко видеть, что либо каждый член является соседом каждого элемента , или никто из примыкает к любому члену . Таким образом, отношения между двумя непересекающимися модулями либо смежный или несмежный. Между этими двумя крайностями не может быть никаких промежуточных отношений.
Из-за этого, модульные перегородки из где каждый класс разбиения является модулем, представляют особый интерес. Предположим представляет собой модульную перегородку. Поскольку классы разбиений не пересекаются, их смежности составляют новый граф, a факторный граф , вершины которого входят в . То есть каждая вершина является модулем группы G, а смежности этих модулей - ребра .
На рисунке ниже вершина 1, вершины с 2 по 4, вершина 5, вершины 6 и 7 и вершины с 8 по 11 представляют собой модульное разбиение. На правой верхней диаграмме ребра между этими наборами изображают частное, данное этим разбиением, а ребра, внутренние по отношению к наборам, изображают соответствующие факторы.
Перегородки и являются тривиальные модульные перегородки. - это просто одновершинный граф, а . Предположим - нетривиальный модуль. потом и одноэлементные подмножества являются нетривиальным модульным разбиением . Таким образом, существование Любые Нетривиальные модули подразумевают существование нетривиальных модульных разбиений. В общем, многие или все члены могут быть нетривиальными модулями.
Если является нетривиальным модулярным разбиением, то компактное представление всех ребер, которые имеют концы в разных классах разбиения . Для каждого класса раздела в , подграф индуцированный называется фактор и дает представление всех ребер с обоими концами в . Следовательно, края можно восстановить только по фактор-графу и его факторы. Период, термин премьер Граф происходит из того факта, что граф простых чисел имеет только тривиальные факторы и факторы.
Когда является фактором модульного частного , Возможно, что можно рекурсивно разложить на множители и частные. Каждый уровень рекурсии дает частное. В базовом случае граф имеет только одну вершину. Коллективно могут быть восстановлены индуктивно, восстанавливая факторы снизу вверх, инвертируя шаги разложения, комбинируя факторы с частным на каждом уровне.
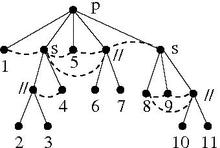
На рисунке ниже такое рекурсивное разложение представлено деревом, которое изображает один из способов рекурсивного разложения факторов исходного модульного раздела на меньшие модульные разделы.
Способ рекурсивного разложения графа на множители и частные может быть не уникальным. (Например, все подмножества вершин полного графа являются модулями, что означает, что существует много различных способов рекурсивного разложения.) Некоторые способы могут быть более полезными, чем другие.
Модульная декомпозиция
К счастью, существует такое рекурсивное разложение графа, которое неявно представляет все способы его разложения; это модульное разложение. Это сам по себе способ рекурсивно разложить граф на частные, но он включает все остальные. Разбиение, изображенное на рисунке ниже, является этим специальным разложением для данного графа.
Следующее - ключевое наблюдение для понимания модульной декомпозиции:
Если это модуль и это подмножество , тогда это модуль , тогда и только тогда, когда это модуль .
В (Галлай, 1967) Галлаи рекурсивно определил модульное разложение на графе с множеством вершин , следующим образом:
- В качестве базового случая, если имеет только одну вершину, его модульная декомпозиция представляет собой единственный узел дерева.
- Галлай показал, что если связно, как и его дополнение, то максимальные модули, являющиеся собственными подмножествами являются разделом . Поэтому они представляют собой модульную перегородку. Частное, которое они определяют, является простым. Корень дерева обозначен как премьер node, и эти модули назначаются как дочерние по отношению к . Поскольку они максимальны, каждый не представленный до сих пор модуль содержится в дочернем из . Для каждого ребенка из , заменяя с модульным деревом разложения дает представление всех модулей , согласно ключевому замечанию выше.
- Если отключено, его дополнение подключено. Каждое объединение компонент связности является модулем . Все остальные модули являются подмножествами одного связного компонента. Это представляет все модули, за исключением подмножеств связанных компонентов. Для каждого компонента , заменяя модульным деревом разложения дает представление всех модулей , согласно ключевому замечанию выше. Корень дерева обозначен как параллельно узел, и он прикрепляется вместо как дочерний элемент корня. Частное, определенное детьми, является дополнением к полному графу.
- Если дополнение отключен, подключен. Поддеревья, являющиеся дочерними определены способом, симметричным случаю, когда отключено, так как модули графа такие же, как модули его дополнения. Корень дерева обозначен как серийный узел, а частное, определенное дочерними элементами, представляет собой полный граф.
Конечное дерево имеет одноэлементные множества вершин как его листья, из-за базового случая. Множество вершин является модулем тогда и только тогда, когда он является узлом дерева или объединением дочерних элементов последовательного или параллельного узла. Это неявно дает всем модульным разделам . Именно в этом смысле дерево модульной декомпозиции "включает" все другие способы рекурсивной декомпозиции. в частные.
Алгоритмические проблемы
Структура данных для представления дерева модульной декомпозиции должна поддерживать операцию, которая вводит узел и возвращает набор вершин что представляет узел. Очевидный способ сделать это - назначить каждому узлу список вершины что он представляет. Учитывая указатель на узел, эта структура может возвращать набор вершин что он представляет в время. Однако для этой структуры данных потребуется пространство в худшем случае.
An -пространственная альтернатива, которая соответствует этой производительности, получается путем представления дерева модульной декомпозиции с использованием любого стандартного структура данных корневого дерева и маркировка каждого листа вершиной что он представляет. Набор представлен внутренним узлом задается набором меток его листовых потомков. Как известно, любое корневое дерево с листья имеет самое большее внутренние узлы. Можно использовать поиск в глубину, начиная с сообщать о метках листовых потомков в время.
Каждый узел набор вершин и если - внутренний узел, множество детей это раздел где каждый класс разбиения является модулем. Следовательно, они индуцируют частное в . Вершины этого частного являются элементами , так можно представить установкой ребер среди детей . Если и два члена и и , тогда и соседствуют в если и только если и смежны в этом частном. Для любой пары вершин , это определяется коэффициентом на детей наименее общего предка и в дереве модульной декомпозиции. Следовательно, модульное разложение, помеченное таким образом факторами, дает полное представление .
Многие комбинаторные задачи решаются на решая задачу отдельно по каждому из этих частных. Например, является графом сопоставимости тогда и только тогда, когда каждое из этих частных является графом сопоставимости (Gallai, 67; Möhring, 85). Следовательно, чтобы определить, является ли граф графом сопоставимости, нужно только выяснить, является ли каждое из частных. Фактически, чтобы найти переходная ориентация графа сравнимости достаточно транзитивно сориентировать каждое из этих частных его модулярного разложения (Gallai, 67; Möhring, 85). Аналогичное явление применяется к графам перестановок (McConnell и Spinrad '94), интервальным графам (Hsu и Ma '99), совершенным графам и другим классам графов. Некоторые важные задачи комбинаторной оптимизации на графах могут быть решены с использованием аналогичной стратегии (Möhring, 85).
Кографы - это графы, которые имеют только параллельные или последовательные узлы в своем модульном дереве декомпозиции.
Первый полиномиальный алгоритм для вычисления дерева модульной декомпозиции графа был опубликован в 1972 году (James, Stanton & Cowan, 1972), и теперь доступны линейные алгоритмы (McConnell & Spinrad 1999, Tedder et al. 2007, Cournier & Habib 1994).
Обобщения
Модульное разложение ориентированных графов может быть выполнено за линейное время (Макконнелл и де Монгольфье 2005).
За небольшим количеством простых исключений каждый граф с нетривиальным модульным разложением также имеет перекос раздела (Рид 2008).
использованная литература
- Галлай, Тибор (1967). "Transitiv orientierbare Graphen". Acta Mathematica Academiae Scientiarum Hungaricae. 18 (1–2): 25–66. Дои:10.1007 / BF02020961. Г-Н 0221974.
- Джеймс, Ли О .; Стэнтон, Ральф Дж .; Коуэн, Дональд Д. (1972). «Графическая декомпозиция для неориентированных графов». Proc. 3-я Юго-Восточная международная конференция по комбинаторике, теории графов и вычислениям (Флоридский Атлантический университет, Бока-Ратон, Флорида, 1972). Атлантический университет Флориды. С. 281–290. Г-Н 0351909.
- Голумбик, Мартин К. (1980). Алгоритмическая теория графов и совершенные графы. Академическая пресса. ISBN 0-444-51530-5.
- Hsu, W.L .; Ма, Т. (1999). «Быстрые и простые алгоритмы распознавания графиков хордовой сопоставимости и интервальных графиков». SIAM Журнал по вычислениям. 28 (3): 1004–1020. CiteSeerX 10.1.1.104.4647. Дои:10.1137 / S0097539792224814.
- МакКоннелл, Росс М .; де Монгольфье, Фабьен (2005). «Модульное разложение ориентированных графов по линейному времени». Дискретная прикладная математика. 145 (2): 198–209. Дои:10.1016 / j.dam.2004.02.017.CS1 maint: ref = harv (ссылка на сайт)
- МакКоннелл, Росс М .; Спинрад, Джереми П. (1999). «Модульная декомпозиция и переходная ориентация» (PDF). Дискретная математика. 201 (1–3): 189–241. Дои:10.1016 / S0012-365X (98) 00319-7. Г-Н 1687819.
- Меринг, Рольф Х. (1985). I. Соперник (ред.). «Алгоритмические аспекты графиков сопоставимости и интервальных графиков». Графики и порядок. Д. Рейдел: 41–101. Дои:10.1007/978-94-009-5315-4_2. ISBN 978-94-010-8848-0.
- Меринг, Рольф Х. (1985). «Алгоритмические аспекты декомпозиции подстановки в оптимизации отношений, систем множеств и булевых функций». Анналы исследований операций. 4: 195–225. Дои:10.1007 / BF02022041.
- Пападопулос, Харис; Фоглис, Константинос (2005). «Рисование графиков с использованием модульной декомпозиции» (PDF). Proc. 13-й Международный симпозиум по графическому рисованию (GD'05). Конспект лекций по информатике. 3843. Springer-Verlag. С. 343–354. Дои:10.1007/11618058_31. Г-Н 2229205.
- Рид, Брюс (2008). «Косые разбиения в совершенных графах» (PDF). Дискретная прикладная математика. 156 (7): 1150–1156. Дои:10.1016 / j.dam.2007.05.054. Г-Н 2404228. Архивировано из оригинал (PDF) в 2015-09-19. Получено 2012-08-13.CS1 maint: ref = harv (ссылка на сайт)
- Спинрад, Джереми П. (2003). Эффективные графические представления. Монографии Института Филдса. Американское математическое общество. ISBN 0-8218-2815-0.
- Теддер, Марк; Корнейл, Дерек; Хабиб, Мишель; Пол, Кристоф (2008). «Более простая модульная декомпозиция линейного времени с помощью рекурсивных факторизационных перестановок». Proc. 35-й Международный коллоквиум по автоматам, языкам и программированию (ICALP 2008). Конспект лекций по информатике. 5125. Springer-Verlag. С. 634–645. arXiv:0710.3901. Дои:10.1007/978-3-540-70575-8_52.
- Захеди, Эмад; Смит, Джейсон (2018). «Модульная декомпозиция графов и свойство сохранения расстояния». Дискретная прикладная математика (7). arXiv:1805.09853. Bibcode:2018arXiv180509853Z.CS1 maint: ref = harv (ссылка на сайт)




![G [X]](https://wikimedia.org/api/rest_v1/media/math/render/svg/14b3dd439dfe0c12fee4dcca2df4daf4ce19727a)































![{ Displaystyle G [X] / P}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d3d19fcdd9b4911906da9cffd9e9195a10325a5)




