WikiDer > Соединение додекаэдра и икосаэдра
| Первая звездчатость икосододекаэдра | |
|---|---|
 | |
| Тип | Двойное соединение |
| Диаграмма Кокстера | |
| Звездчатость основной | икосододекаэдр |
| Выпуклый корпус | Ромбический триаконтаэдр |
| Индекс | W47 |
| Многогранники | 1 икосаэдр 1 додекаэдр |
| Лица | 20 треугольники 12 пятиугольники |
| Края | 60 |
| Вершины | 32 |
| Группа симметрии | икосаэдр (ячас) |
В геометрия, этот многогранник можно рассматривать как многогранник звездчатость или сложный.
Как соединение
Это можно рассматривать как сложный из икосаэдр и додекаэдр. Это одно из четырех комплексов, построенных из Платоново твердое тело или же Твердое тело Кеплера-Пуансо, и это двойной.
Она имеет икосаэдрическая симметрия (ячас) и то же расположение вершин как ромбический триаконтаэдр.
Это можно рассматривать как трехмерный эквивалент соединения двух пятиугольников ({10/2} "декаграмма"); эта серия продолжается в четвертом измерении как соединение из 120 и 600 ячеек и в более высокие измерения как соединения гиперболических мозаик.
Додекаэдр и его двойной икосаэдр |
Десятиугольник справа - это Многоугольник Петри обоих твердых тел.
Как звездочка
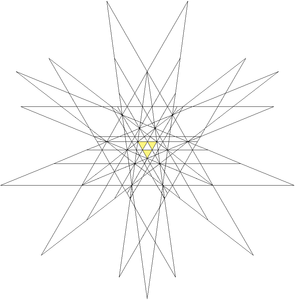
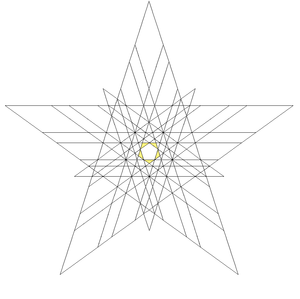
Этот многогранник это первый звездчатость из икосододекаэдр, и задано как Индекс модели Веннингера 47.
Звездчатые грани для строительства:
В популярной культуре
В фильме Трон (1982), персонаж Кусочек принял эту форму, когда не говорил.
В мультсериале Вселенная Стивена (2013-2019), Розовый Стивенщитовой пузырь, кратко использованный в эпизоде Измени свое мнение, имел такую форму.
Смотрите также
- Соединение двух тетраэдров
- Соединение куба и октаэдра
- Соединение малого звездчатого додекаэдра и большого додекаэдра
- Соединение большого звездчатого додекаэдра и большого икосаэдра
Рекомендации
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9.