WikiDer > Ромбический триаконтаэдр
Эта статья включает в себя список общих использованная литература, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. (Декабрь 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
| Ромбический триаконтаэдр | |
|---|---|
 (Нажмите здесь, чтобы повернуть модель) | |
| Тип | Каталонский твердый |
| Диаграмма Кокстера | |
| Обозначение Конвея | jD |
| Тип лица | V3.5.3.5 ромб |
| Лица | 30 |
| Края | 60 |
| Вершины | 32 |
| Вершины по типу | 20{3}+12{5} |
| Группа симметрии | ячас, H3, [5,3], (*532) |
| Группа вращения | Я, [5,3]+, (532) |
| Двугранный угол | 144° |
| Свойства | выпуклый, лицо переходный равногранный, изотоксальный, зоноэдр |
 Икосододекаэдр (двойственный многогранник) |  Сеть |
В геометрия, то ромбический триаконтаэдр, иногда просто называют триаконтаэдр так как это самый распространенный тридцатигранный многогранник, это выпуклый многогранник с 30 ромбический лица. Имеет 60 края и 32 вершины двух типов. Это Каталонский твердый, а двойственный многогранник из икосододекаэдр. Это зоноэдр.
 Грань ромбического триаконтаэдра. Длина диагоналей находятся в Золотое сечение. |

Отношение длинной диагонали к короткой диагонали каждой грани в точности равно Золотое сечение, φ, таким образом острые углы по каждому лицу измерять 2 загар−1(1/φ) = загар−1(2), или примерно 63,43 °. Полученный таким образом ромб называется золотой ромб.
Будучи двойником Архимедово твердое тело, ромбический триаконтаэдр лицо переходный, имея в виду группа симметрии твердых актов переходно на множестве лиц. Это означает, что для любых двух граней A и B существует вращение или отражение твердого тела, которое покидает его, занимая ту же область пространства, перемещая грань A на грань B.
Ромбический триаконтаэдр является одним из девяти реберно-транзитивный выпуклые многогранники, остальные пять Платоновы тела, то кубооктаэдр, то икосододекаэдр, а ромбический додекаэдр.
Ромбический триаконтаэдр интересен еще и тем, что в его вершинах расположены четыре Платоновых тела. Он содержит десять тетраэдры, 5 кубики, икосаэдр и додекаэдр. Центры граней содержат пять октаэдры.
Его можно сделать из усеченный октаэдр разделив шестиугольные грани на 3 ромба:

Декартовы координаты
Позволять быть Золотое сечение. 12 баллов, присвоенных а циклические перестановки этих координат являются вершинами правильный икосаэдр. Его двойная правильный додекаэдр, чьи ребра пересекаются с ребрами икосаэдра под прямым углом, имеет в качестве вершин 8 точек вместе с 12 точками и циклические перестановки этих координат. Все 32 точки вместе являются вершинами ромбического триаконтаэдра с центром в начале координат. Длина его краев . Его грани имеют диагонали с длиной. и .
Габаритные размеры
Если длина ребра ромбического триаконтаэдра равна а, площадь поверхности, объем, радиус из вписанная сфера (касательная к каждой из граней ромбического триаконтаэдра) и средний радиус, который касается середины каждого ребра:[1]
где φ это Золотое сечение.
В вдохновлять касается граней в центроидах их граней. Короткие диагонали принадлежат только ребрам вписанного правильного додекаэдра, а длинные диагонали включены только ребрам вписанного икосаэдра.
Рассечение
Ромбический триаконтаэдр можно разрезать на 20 частей. золотые ромбоэдры: 10 острых и 10 тупых.[2][3]
| 10 | 10 |
|---|---|
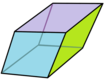 Острая форма |  Тупая форма |
Ортогональные проекции
Ромбический триаконтаэдр имеет четыре положения симметрии: два с центрами вершин, одну среднюю грань и одну среднюю грань. В проекцию «10» встроены «толстый» ромб и «тощий» ромб, которые соединяются вместе для создания непериодической мозаики, часто называемой Плитка Пенроуза.
| Проективный симметрия | [2] | [2] | [6] | [10] |
|---|---|---|---|---|
| Образ |  |  |  |  |
| Двойной образ |  |  |  |  |
Звёздчатые
Ромбический триаконтаэдр имеет 227 полностью опорных звездчатых элементов.[4][5] Другая звездчатая форма ромбического триаконтаэдра - это соединение пяти октаэдров. Общее количество звёздчатых звёзд ромбического триаконтаэдра составляет 358 833 097.
Связанные многогранники
| Семейство однородных икосаэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия: [5,3], (*532) | [5,3]+, (532) | ||||||
 |  |  |  |  |  |  |  |
| {5,3} | т {5,3} | г {5,3} | т {3,5} | {3,5} | рр {5,3} | tr {5,3} | ср {5,3} |
| Двойники к однородным многогранникам | |||||||
 |  |  |  |  | |||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Этот многогранник является частью последовательности ромбические многогранники и мозаики с [п,3] Группа Кокстера симметрия. Куб можно рассматривать как ромбический шестигранник, в котором ромбы также являются прямоугольниками.
| Мутации симметрии двойственных квазирегулярных мозаик: V (3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| * n32 | Сферический | Евклидово | Гиперболический | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Плитка |  |  |  |  |  |  |  | ||||
| Конф. | В (3,3)2 | V (3,4)2 | В (3,5)2 | В (3,6)2 | В (3,7)2 | V (3.8)2 | V (3.∞)2 | ||||
Ромбический триаконтаэдр с вписанным тетраэдром (красный) и куб (желтый).
(Нажмите здесь, чтобы повернуть модель)Ромбический триаконтаэдр с вписанным додекаэдром (синий) и икосаэдр (фиолетовый).
(Нажмите здесь, чтобы повернуть модель)
6-куб
Ромбический триаконтаэдр образует 32 вершины выпуклая оболочка одной проекции 6-куб до трех измерений.
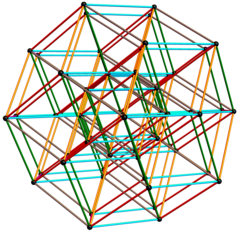 Трехмерные базисные векторы [u, v, w]:
| Показано со скрытыми внутренними краями 20 из 32 внутренних вершин образуют додекаэдр, а остальные 12 образуют икосаэдр. |
Использует
Датский дизайнер Хольгер Стрём использовал ромбический триаконтаэдр в качестве основы для дизайна своей сборной лампы IQ-light (IQ от «Переплетенные четырехугольники»).

Мастерица по дереву Джейн Костик строит коробки в форме ромбического триаконтаэдра.[6] Простая конструкция основана на менее чем очевидной связи между ромбическим триаконтаэдром и кубом.
Роджер фон Ох"Ball of Whacks" имеет форму ромбического триаконтаэдра.
Ромбический триаконтаэдр используется как "d30"тридцатигранная кость, иногда полезная в некоторых ролевые игры игры или другие места.
Кристофер Берд, соавтор Тайная жизнь растений написал статью для New Age Journal в мае 1975 года, популяризируя двойной икосаэдр и додекаэдр как «кристаллическую структуру Земли», модель «Земной (теллурической) Энергетической Решетки». Планета EarthStar Globe Билла Беккера и Бете А. Хагенс призвана показать «естественную геометрию Земли и геометрические отношения между священными местами, такими как Великая пирамида, Бермудский треугольник и остров Пасхи». Он напечатан в виде ромбического триаконтаэдра на 30 бриллиантах и складывается в шар.[7]
Смотрите также
использованная литература
- ^ Стивен Вольфрам, "[1]" от вольфрам Альфа. Проверено 7 января 2013 года.
- ^ [2]
- ^ Рассечение ромбического триаконтаэдра
- ^ Поули, Г. С. (1975). «227 триаконтаэдров». Geometriae Dedicata. Kluwer Academic Publishers. 4 (2–4): 221–232. Дои:10.1007 / BF00148756. ISSN 1572-9168.
- ^ Мессер, П. В. (1995). «Звёздчатые формы ромбического триаконтаэдра и за его пределами». Структурная топология. 21: 25–46.
- ^ коробка триаконтаэдра - KO Sticks LLC
- ^ http://www.vortexmaps.com/grid-history.php
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 0-486-23729-X. (Раздел 3-9)
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, Дои:10.1017 / CBO9780511569371, ISBN 978-0-521-54325-5, Г-Н 0730208 (Тринадцать полуправильных выпуклых многогранников и их двойники, стр. 22, Ромбический триаконтаэдр)
- Симметрии вещей 2008, Джон Х. Конвей, Хайди Берджел, Хаим Гудман-Штрасс, ISBN 978-1-56881-220-5 [3] (Глава 21, Именование архимедовых и каталонских многогранников и мозаик, стр. 285, Ромбический триаконтаэдр)
внешние ссылки
- Эрик В. Вайсштейн, Ромбический триаконтаэдр (Каталонский твердый) в MathWorld.
- Ромбический триаконтраэдр - Интерактивная модель многогранника
- Многогранники виртуальной реальности - Энциклопедия многогранников
- Звёздчатые формы ромбического триаконтаэдра.
- Земной шар EarthStar - проекция карты ромбического триаконтаэдра
- IQ-свет- лампа датского дизайнера Хольгера Стрёма.
- Сделать свой собственный
- деревянная конструкция коробки ромбического триаконтаэдра - плотник Джейн Костик
- 120 ромбических триаконтаэдров, 30 + 12 ромбических триаконтаэдров, и 12 ромбических триаконтаэдров Шандор Кабаи, Демонстрационный проект Wolfram
- Змея, нарисованная на ромбическом триаконтаэдре.
























































