WikiDer > Перекрещенный пятиугольный куплоид
| Перекрещенный пятиугольный куплоид | |
|---|---|
 | |
| Лица | 5 треугольники 5 квадраты 1 пятиугольник |
| Края | 20 |
| Вершины | 10 |
| Конфигурация вершины | 5(5.4.3/2.4) 5(3.4.3/2.4/3) |
| Группа симметрии | C5в, [5], (*55) |
| Группа вращения | C5, [5]+, (55) |
| Двойной многогранник | скрещенный пятиугольный кератиноид |
| Характеристики | неориентируемый |
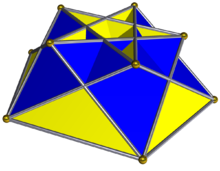
В геометрия, то скрещенный пятиугольный куполоид или же скрещенная пятиугольная полукупола один из членов бесконечной семьи куплоиды. Его можно получить как кусок большой сложный ромбикосододекаэдр. Как и во всех купола, база многоугольник вдвое больше края и вершины как верхний; но в этом случае базовый многоугольник является вырожденным {10/4} декаграмма, так как верх - это {5/4} пятиугольник. Следовательно, вырожденное основание удаляется, и вместо этого треугольники соединяются с квадратами.
Его можно рассматривать как купол с ретроградным пятиугольным основанием, так что квадраты и треугольники соединяются через основания в противоположном направлении от основания. пятиугольный купол, следовательно, пересекаются друг с другом.
Связанные многогранники
| п⁄d | 3 | 5 | 7 |
|---|---|---|---|
| 2 |  Перекрещенный треугольный куплоид |  Пентаграмматический куплоид |  Гептаграмматический куплоид |
| 4 | — |  Перекрещенный пятиугольный куплоид |  Скрещенный гептаграммный куплоид |
Скрещенный пятиугольный куплоид можно рассматривать как часть вырожденного однородного многогранника, известного как большой сложный ромбикосододекаэдр:
 Перекрещенный пятиугольный куплоид |  Большой сложный ромбикосододекаэдр | ||
 Малый дитригональный икосододекаэдр |  Дитригональный додекадодекаэдр |  Большой дитригональный икосододекаэдр |  Соединение пяти кубиков |
(На изображении скрещенного пятиугольного куплоида пятиугольник красный (внизу и не виден), квадраты желтые, а треугольники синие. На изображении небольшого сложного ромбоикосододекаэдра пятиугольники красные, квадраты синие ( скрыты внутри и не видны), а треугольники желтые.)
Если взять один пятиугольник из большого сложного ромбикосододекаэдра, затем взять пять соседних с ним квадратов, затем взять пять треугольников, граничащих с этими квадратами, получится скрещенный пятиугольный куплоид. Так как этот скрещенный пятиугольный куплоид, таким образом, имеет все стороны с этим многогранником, его можно назвать край-огранка этого. Невырожденные однородные многогранники, имеющие те же ребра, что и небольшой сложный ромбикосододекаэдр, представляют собой три дитригональные многогранники, а также обычный соединение пяти кубиков: следовательно, скрещенный пятиугольный куплоид также является гранью этих многогранников.
В качестве 5/4 <2, у скрещенного пятиугольного куплоида нет мембраны, как у пентаграмматического куплоида.
Двойной многогранник
Двойник скрещенного пятиугольного куплоида имеет 5 воздушных змеев и 5 воздушных змеев. антипараллелограмм лица, и может быть назван скрещенный пятиугольный кератиноид после Inchbald, из-за того, что он имеет форму полого рога:
Рекомендации
- Гай Инчбальд, Заполнение многогранников
- Ричард Клитцинг, Осесимметричные грани равномерных многогранников.
- Джим Макнил, Полукупола 5/2 и полукупола 5/4
- Джим Макнил, Полукупола
- Ульрих Микловейт, Гранки однородных многогранников


