WikiDer > Кристаллографическая теорема ограничения
Эта статья отсутствует информация о лаконичной формулировке теоремы. (Декабрь 2018 г.) |
В кристаллографическая теорема ограничения в своей основной форме было основано на наблюдении, что вращательная симметрия из кристалл обычно ограничиваются 2-кратным, 3-кратным, 4-кратным и 6-кратным. Тем не мение, квазикристаллы может иметь место с другой симметрией дифракционной картины, например с 5-кратной; они не были обнаружены до 1982 г. Дэн Шехтман.[1]
Кристаллы моделируются дискретными решетки, созданный списком независимый конечный переводы (Кокстер 1989). Поскольку дискретность требует, чтобы расстояния между точками решетки имели нижнюю границу, группа вращательной симметрии решетки в любой точке должна быть конечная группа (в качестве альтернативы, точка - единственная система, допускающая бесконечную симметрию вращения). Сила теоремы в том, что не все конечные группы совместимы с дискретной решеткой; в любом измерении у нас будет только конечное число совместимых групп.
Размеры 2 и 3
Частные случаи 2D (группы обоев) и 3D (космические группы) наиболее активно используются в приложениях, и их можно рассматривать вместе.
Решетка доказательство
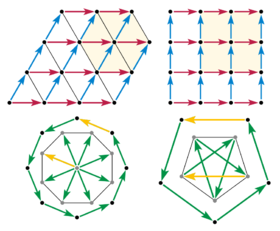
Симметрия вращения в размерности 2 или 3 должна перемещать точку решетки в преемственность других точек решетки в той же плоскости, порождая правильный многоугольник точек компланарной решетки. Теперь мы ограничимся рассмотрением плоскости, в которой действует симметрия (Шеррер 1946), проиллюстрированный решеткой векторов на рисунке.
Теперь рассмотрим 8-кратный поворот и векторы смещения между соседними точками многоугольника. Если между любыми двумя точками решетки существует смещение, то такое же смещение повторяется везде в решетке. Итак, соберите все смещения краев, чтобы начать с одной точки решетки. В рёберные векторы становятся радиальными векторами, и их 8-кратная симметрия подразумевает правильный восьмиугольник из точек решетки вокруг точки сбора. Но это невозможно, потому что новый восьмиугольник примерно на 80% больше оригинала. Значение сжатия в том, что оно безгранично. Эту же конструкцию можно повторять с новым восьмиугольником, и снова и снова, пока расстояние между точками решетки не станет настолько маленьким, насколько нам нравится; таким образом, нет дискретный решетка может иметь 8-кратную симметрию. Тот же аргумент применим к любому k-кратное вращение, для k больше 6.
Аргумент сокращения также устраняет 5-кратную симметрию. Рассмотрим правильный пятиугольник из точек решетки. Если он существует, то мы можем взять каждый Другой смещение края и (голова к хвосту) собрать 5-конечную звезду, причем последний край возвращается в исходную точку. Вершины такой звезды снова являются вершинами правильного пятиугольника с 5-кратной симметрией, но примерно на 60% меньше исходного.
Таким образом, теорема доказана.
Существование квазикристаллов и Мозаики Пенроуза показывает, что предположение о линейном переносе необходимо. У мозаик Пенроуза может быть 5-кратное вращательная симметрия и дискретная решетка, и любая локальная окрестность мозаики повторяется бесконечно много раз, но нет линейного переноса для мозаики в целом. А без предположения о дискретной решетке вышеупомянутая конструкция не только не приводит к противоречию, но и дает (недискретный) контрпример. Таким образом, 5-кратная вращательная симметрия не может быть устранена аргументом, в котором отсутствует какое-либо из этих предположений. Замощение Пенроуза всей (бесконечной) плоскости может иметь точную 5-кратную вращательную симметрию (всего разбиения) относительно одной точки, в то время как 4-кратная и 6-кратная решетки имеют бесконечно много центров вращательной симметрии.
Доказательство тригонометрии
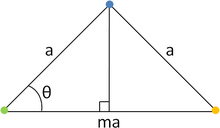
Рассмотрим две точки решетки A и B, разделенные вектором сдвига р. Рассмотрим угол α такой, что поворот на угол α относительно любой точки решетки является симметрией решетки. Вращение вокруг точки B на α отображает точку A в новую точку A '. Аналогично, поворот вокруг точки A на α отображает B в точку B '. Поскольку оба упомянутых поворота являются операциями симметрии, A 'и B' должны быть точками решетки. Из-за периодичности кристалла новый вектор р' который их связывает, должно быть целым числом, кратным р:
с целое число. Четыре вектора трансляции, три из которых имеют длину и один, соединяющий A 'и B', длиной , образуют трапецию. Следовательно, длина р' также определяется:
Объединение двух уравнений дает:
куда также является целым числом. Имея в виду, что мы разрешили целые числа . Решение возможных значений показывает, что единственными значениями в диапазоне от 0 ° до 180 ° являются 0 °, 60 °, 90 °, 120 ° и 180 °. В радианах единственные разрешенные вращения, совместимые с периодичностью решетки, равны 2π /п, куда п = 1, 2, 3, 4, 6. Это соответствует 1-, 2-, 3-, 4- и 6-кратной симметрии соответственно и, следовательно, исключает возможность 5-кратной или более чем 6-кратной симметрии. .
Краткое тригонометрическое доказательство
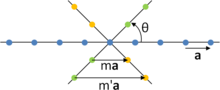
Рассмотрим линию атомов A-O-B, разделенные расстоянием а. Повернуть всю строку на θ = + 2π /п и θ = −2π /п, с точкой О фиксируется. После поворота на + 2π /п, A перемещается в точку решетки C а после поворота на -2π /п, B перемещается в точку решетки D. Из-за предполагаемой периодичности решетки две точки решетки C и D будет также в строке непосредственно под начальной строкой; более того C и D будут разделены р = ма, с м целое число. Но по геометрии расстояние между этими точками составляет:
- .
Приравнивание этих двух отношений дает:
Этого удовлетворяет только п = 1, 2, 3, 4, 6.
Матричное доказательство
Для альтернативного доказательства рассмотрим матрица характеристики. Сумма диагональных элементов матрицы называется след матрицы. В 2D и 3D каждое вращение является плоскостным вращением, и след является функцией только угла. Для двухмерного вращения след равен 2 cos θ; для трехмерного вращения 1 + 2 cos θ.
Примеры
- Рассмотрим 60 ° (6-кратное) матрица вращения в отношении ортонормированный базис в 2D.
- След ровно 1, целое число.
- Рассмотрим матрицу поворота на 45 ° (8-кратную).
- След 2 /√2, а не целое число.
Выбор базиса, образованного из векторов, охватывающих решетку, не гарантирует ни ортогональности, ни единичной длины, только линейную независимость. Однако след матрицы вращения одинаков для любого базиса. След - это инвариант подобия при линейных преобразованиях. В базисе решетки операция вращения должна отображать каждую точку решетки в целое число векторов решетки, поэтому элементы матрицы вращения в базисе решетки - и, следовательно, след - обязательно являются целыми числами. Как и в других доказательствах, это означает, что единственные разрешенные симметрии вращения соответствуют 1,2,3,4 или 6-кратной инвариантности. Например, обои и кристаллы не могут поворачиваться на 45 ° и оставаться неизменными, возможны только углы: 360 °, 180 °, 120 °, 90 ° или 60 °.
Пример
- Рассмотрим матрицу поворота на 60 ° (360 ° / 6) относительно косой решетчатая основа для черепица равносторонними треугольниками.
- След по-прежнему 1. детерминант (всегда +1 за поворот) также сохраняется.
Общее кристаллографическое ограничение на вращение делает нет гарантировать, что вращение будет совместимо с определенной решеткой. Например, поворот на 60 ° не подойдет для квадратной решетки; и поворот на 90 ° не будет работать с прямоугольной решеткой.
Высшие измерения
Когда размер решетки увеличивается до четырех или более, повороты больше не должны быть плоскими; 2D-доказательство неадекватно. Однако ограничения по-прежнему действуют, хотя допускается большее количество симметрий. Например, гиперкубическая решетка имеет восьмеричную вращательную симметрию, соответствующую восьмикратной вращательной симметрии гиперкуб. Это представляет интерес не только для математики, но и для физики квазикристаллов в условиях теория сокращения и проекта. С этой точки зрения трехмерный квазикристалл с 8-кратной симметрией вращения может быть описан как проекция пластины, вырезанной из четырехмерной решетки.
Следующая 4-мерная матрица вращения представляет собой вышеупомянутую восьмеричную симметрию гиперкуб (и кросс-многогранник):
Преобразование этой матрицы в новые координаты, заданные
- произведет:
Эта третья матрица соответствует повороту как на 45 ° (в первых двух измерениях), так и на 135 ° (в последних двух). Проецирование плиты гиперкубов по первым двум измерениям новых координат дает Мозаика Амманна – Бенкера (еще одна такая мозаика получается путем проецирования по последним двум измерениям), которая, следовательно, также имеет в среднем 8-кратную вращательную симметрию.
В Решетка А4 и Решетка F4 имеют вращательную симметрию порядка 10 и порядка 12 соответственно.
Чтобы сформулировать ограничение для всех измерений, удобно отвлечь внимание от одних только вращений и сосредоточиться на целочисленных матрицах (Бамберг, Кэрнс и Килминстер 2003). Мы говорим, что матрица A имеет порядок k когда это k-я степень (но не ниже), Аk, равняется тождеству. Таким образом, матрица шестикратного вращения в базисе равностороннего треугольника является целочисленной матрицей порядка 6. Пусть OrdN обозначают набор целых чисел, которые могут быть порядком N×N целочисленная матрица. Например, Ord2 = {1, 2, 3, 4, 6}. Мы хотим сформулировать явную формулу для OrdN.
Определим функцию ψ на основе Функция Эйлера φ; он будет отображать положительные целые числа в неотрицательные целые числа. Для нечетного основной, п, и положительное целое число, k, положим ψ (пk) равной значению общей функции φ (пk), которая в данном случае пk−пк − 1. Сделайте то же самое для ψ (2k) когда k > 1. Установите ψ (2) и ψ (1) в 0. Используя основная теорема арифметики, мы можем записать любое другое положительное целое однозначно как произведение степеней простых чисел, м = ∏α пαk α; положим ψ (м) = ∑α ψ (пαk α). Это отличается от самого totient, потому что это сумма, а не продукт.
Кристаллографическое ограничение в общем виде утверждает, что OrdN состоит из этих положительных целых чисел м такое, что ψ (м) ≤ N.
Наименьший размер для данного заказаOEIS: A080737 м 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 ψ (м) 0 0 2 2 4 2 6 4 6 4 10 4 12 6 6 8 16 6 18 6 8 10 22 6 20 12 18 8 28 6 30
За м> 2 значения ψ (м) равны удвоенному алгебраическая степень из cos (2π /м); поэтому ψ (м) строго меньше, чем м и достигает этого максимального значения тогда и только тогда, когда м это основной.
Эти дополнительные симметрии не позволяют плоскому срезу иметь, скажем, 8-кратную симметрию вращения. В плоскости все еще действуют ограничения 2D. Таким образом, вырезы, используемые для моделирования квазикристаллов, обязательно имеют толщину.
Целочисленные матрицы не ограничиваются поворотами; например, отражение также является симметрией порядка 2. Но, настаивая на определителе +1, мы можем ограничить матрицы до правильные вращения.
Формулировка в терминах изометрий
Кристаллографическая теорема об ограничении может быть сформулирована в терминах изометрии из Евклидово пространство. Набор изометрий может образовать группа. Автор группа дискретной изометрии мы будем иметь в виду группу изометрий, которая отображает каждую точку в дискретное подмножество рN, т.е. орбита любой точки представляет собой набор изолированные точки. Используя эту терминологию, кристаллографическая теорема ограничения в двух и трех измерениях может быть сформулирована следующим образом.
- Для каждого дискретного группа изометрии в двух- и трехмерном пространстве, которое включает трансляции, охватывающие все пространство, все изометрии конечных порядок имеют порядок 1, 2, 3, 4 или 6.
Изометрии порядка п включать, но не ограничиваться, п-кратные вращения. Теорема также исключает S8, S12, D4d, и D6d (видеть группы точек в трех измерениях), хотя они обладают только 4- и 6-кратной вращательной симметрией. Вращательная симметрия любого порядка относительно оси совместима с трансляционной симметрией вдоль этой оси.
Результат в таблице выше означает, что для каждой дискретной группы изометрий в четырех- и пятимерном пространстве, которая включает трансляции, охватывающие все пространство, все изометрии конечного порядка имеют порядок 1, 2, 3, 4, 5, 6, 8. , 10 или 12.
Все изометрии конечного порядка в шестимерном и семимерном пространстве имеют порядок 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 или 30.
Смотрите также
Примечания
- ^ Шехтман и др. (1982)
Рекомендации
- Бамберг, Джон; Кэрнс, Грант; Килминстер, Девин (март 2003 г.), «Кристаллографическое ограничение, перестановки и гипотеза Гольдбаха» (PDF), Американский математический ежемесячный журнал, 110 (3): 202–209, CiteSeerX 10.1.1.124.8582, Дои:10.2307/3647934, JSTOR 3647934
- Эллиот, Стивен (1998), Физика и химия твердого тела, Wiley, ISBN 978-0-471-98194-7
- Кокстер, Х. С. М. (1989), Введение в геометрию (2-е изд.), Wiley, ISBN 978-0-471-50458-0
- Шеррер, В. (1946), "Die Einlagerung eines Regären Vielecks in ein Gitter", Elemente der Mathematik, 1 (6): 97–98
- Шехтман, Д .; Blech, I .; Gratias, D .; Кан, Дж. У. (1984), "Металлическая фаза с дальним ориентационным порядком и без трансляционной симметрии", Письма с физическими проверками, 53 (20): 1951–1953, Bibcode:1984ПхРвЛ..53.1951С, Дои:10.1103 / PhysRevLett.53.1951