WikiDer > Направленный ациклический граф

Directed acyclic graph

А топологический порядок ориентированного ациклического графа: каждые край идет от более раннего в порядке (вверху слева) к более позднему в порядке (внизу справа). Ориентированный граф ацикличен тогда и только тогда, когда он имеет топологический порядок.

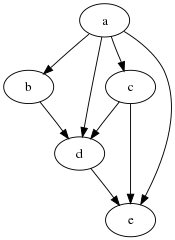
В математика, особенно теория графов, и Информатика, а ориентированный ациклический граф (DAG или даг /ˈdæɡ/ (Об этом звукеСлушать)) это ориентированный граф без направленные циклы. То есть состоит из вершины и края (также называемый дуги), причем каждое ребро направлено от одной вершины к другой, так что нет возможности начать с любой вершины v и следуйте последовательно направленной последовательности ребер, которая в конечном итоге возвращается к v опять таки. Эквивалентно DAG - это ориентированный граф, имеющий топологический порядок, последовательность вершин такая, что каждое ребро направлено от более раннего к более позднему в последовательности.

Группы DAG могут моделировать множество различных видов информации. Например, электронная таблица может быть смоделирован как группа DAG с вершиной для каждой ячейки и ребром, когда формула в одной ячейке использует значение из другой; топологический порядок этого DAG может использоваться для обновления всех значений ячеек при изменении электронной таблицы. Точно так же топологический порядок DAG может использоваться для упорядочивания операций компиляции в makefile. В методика оценки и обзора программ (PERT) использует группы доступности базы данных для моделирования основных этапов и действий крупных человеческих проектов и составляет график этих проектов, чтобы использовать как можно меньше общего времени. Комбинационная логика блоки в конструкции электронных схем, а операции в программирование потока данных языки, включают ациклические сети элементов обработки. Группы DAG также могут представлять совокупность событий и их влияние друг на друга либо в виде вероятностной структуры, например, Байесовская сеть или как запись исторических данных, таких как родословные или истории версий распределенный контроль версий системы. Группы DAG также можно использовать как компактное представление данных последовательности, таких как направленный ациклический граф слов представление коллекции строк или диаграмма двоичных решений представление последовательностей бинарных выборов. Говоря более абстрактно, достижимость отношение в DAG образует частичный заказ, и любые конечный частичный порядок может быть представлен группой DAG с использованием достижимости.

Важный полиномиальное время вычислительные проблемы на DAG включают топологическая сортировка (вычисление топологического упорядочения), построение переходное закрытие и переходная редукция (наибольший и наименьший группы DAG с одинаковым отношением достижимости соответственно) наборов, а проблема закрытия, цель которого - найти подмножество вершин с минимальным весом без ребер, соединяющих их с остальной частью графа. Преобразование ориентированного графа с циклами в DAG путем удаления как можно меньшего количества вершин или ребер ( набор вершин обратной связи и набор кромок обратной связи проблема соответственно) является NP-жесткий проблема, но любой ориентированный граф можно превратить в DAG (его конденсация) путем заключения контракта с каждым компонент сильной связности в единую супервершину. Проблемы поиска кратчайшие пути и самые длинные пути можно решить на DAG в линейное время, в отличие от произвольных графов, для которых алгоритмы кратчайшего пути медленнее, а задачи с самым длинным путем NP-трудны.

Соответствующая концепция для неориентированные графы это лес, неориентированный граф без циклов. Выбор ориентации для леса дает особый вид ориентированного ациклического графа, называемый многодерево. Однако не каждый ориентированный ациклический граф соответствует ориентации ребер неориентированного ациклического графа. В конце концов, любой неориентированный граф, циклический или ациклический, имеет ациклическая ориентация, задание направления для его ребер, которое превращает его в ориентированный ациклический граф. Чтобы подчеркнуть, что DAG - это не то же самое, что направленные версии неориентированных ациклических графов, некоторые авторы называют их ациклические ориентированные графы[1] или ациклические диграфы.[2]

Определения

А график формируется вершины и по края соединяющие пары вершин, где вершинами могут быть любые объекты, которые попарно соединены ребрами. В случае ориентированный граф, каждое ребро имеет ориентацию от одной вершины к другой вершине. А дорожка в ориентированном графе - это последовательность ребер, обладающая тем свойством, что конечная вершина каждого ребра в последовательности совпадает с начальной вершиной следующего ребра в последовательности; путь образует цикл, если начальная вершина его первого ребра равна конечной вершине его последнего ребра. Ориентированный ациклический граф - это ориентированный граф без циклов.[1][2][3]

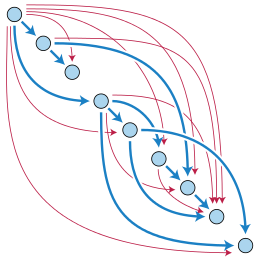
Добавление красных ребер к синему ориентированному ациклическому графу дает еще один DAG, переходное закрытие синего графика. Для каждого красного или синего края УФ, v является достижимый из ты: существует синий путь, начинающийся в ты и заканчивая v.

Вершина v ориентированного графа называется достижимый из другой вершины ты когда существует путь, который начинается в ты и заканчивается в v. Как частный случай, каждая вершина считается достижимой из самой себя (путем с нулевыми ребрами). Если вершина может достичь себя через нетривиальный путь (путь с одним или несколькими ребрами), то этот путь является циклом, поэтому другой способ определения ориентированных ациклических графов состоит в том, что они представляют собой графы, в которых ни одна вершина не может достичь себя через нетривиальный путь.[4]

А топологический порядок ориентированного графа - это упорядочение его вершин в последовательность, так что для каждого ребра начальная вершина ребра встречается раньше в последовательности, чем конечная вершина ребра. Граф, имеющий топологический порядок, не может иметь никаких циклов, потому что край в самой ранней вершине цикла должен быть ориентирован неправильно. Следовательно, любой граф с топологическим порядком является ациклическим. И наоборот, каждый ориентированный ациклический граф имеет по крайней мере один топологический порядок. Следовательно, это свойство можно использовать как альтернативное определение ориентированных ациклических графов: это как раз те графы, которые имеют топологический порядок.[2]

Математические свойства

Достижимость, переходное замыкание и переходное сокращение

В достижимость отношения в любом ориентированном ациклическом графе можно формализовать как частичный заказ ≤ на вершинах DAG. В этом частичном порядке две вершины ты и v заказываются как ты ≤ v именно тогда, когда существует направленный путь от ты к v в DAG; то есть когда v доступен из ты.[5] Однако разные группы DAG могут привести к одному и тому же отношению достижимости и одному и тому же частичному порядку.[6] Например, DAG с двумя гранями а → б и б → c имеет то же отношение достижимости, что и граф с тремя ребрами а → б, б → c, и а → c. Оба этих DAGS производят одинаковый частичный порядок, в котором вершины упорядочены как а ≤ б ≤ c.

Если грамм это DAG, его переходное закрытие - это граф с наибольшим количеством ребер, который представляет одно и то же отношение достижимости. У него есть преимущество ты → v всякий раз, когда ты может достигать v. То есть у него есть преимущество для каждой связанной пары ты ≤ v различных элементов в отношении достижимости грамм, и поэтому может рассматриваться как прямой перевод отношения достижимости ≤ в терминах теории графов. Тот же метод преобразования частичных заказов в DAG работает в более общем плане: для каждого конечного частично упорядоченного набора (S, ≤), граф, имеющий вершину для каждого члена S и ребро для каждой пары элементов, связанных ты ≤ v автоматически является транзитивно закрытым DAG и имеет (S, ≤) как отношение его достижимости. Таким образом, каждый конечный частично упорядоченный набор может быть представлен как отношение достижимости DAG.

DAG грамм
Переходное сокращение грамм

В переходная редукция группы DAG грамм - граф с наименьшим количеством ребер, который представляет то же отношение достижимости, что и грамм. Это подграф грамм, образованный отбрасыванием краев ты → v для которого грамм также содержит более длинный путь, соединяющий те же две вершины. Подобно транзитивному замыканию, транзитивное сокращение однозначно определено для DAG. Напротив, для ориентированного графа, который не является ациклическим, может быть более одного минимального подграфа с одним и тем же отношением достижимости.[7]

А Диаграмма Хассе представляющий частичный порядок включения множества (⊆) среди подмножеств трехэлементного множества.

Если DAG грамм имеет отношение достижимости, описываемое частичным порядком ≤, то транзитивное сокращение грамм является подграфом грамм что имеет преимущество ты → v для каждой пары в покрывающее отношение из ≤. Транзитивные редукции полезны для визуализации частичных порядков, которые они представляют, поскольку у них меньше ребер, чем у других графов, представляющих те же порядки, и поэтому они приводят к более простым графические рисунки. А Диаграмма Хассе частичного порядка - это рисунок переходной редукции, в котором ориентация каждого ребра показана путем размещения начальной вершины ребра в более низком положении, чем его конечная вершина.[8]

Топологический порядок

Каждый ориентированный ациклический граф имеет топологический порядок, такой порядок вершин, что начальная конечная точка каждого ребра встречается раньше, чем конечная конечная точка ребра. Существование такого порядка можно использовать для характеристики групп DAG: ориентированный граф является DAG тогда и только тогда, когда он имеет топологическое упорядочение. В общем, этот порядок не уникален; DAG имеет уникальный топологический порядок тогда и только тогда, когда он имеет направленный путь, содержащий все вершины, и в этом случае порядок такой же, как и порядок, в котором вершины появляются в пути.[9]

Семейство топологических порядков DAG такое же, как и семейство линейные расширения отношения достижимости для DAG,[10] поэтому любые два графа, представляющие один и тот же частичный порядок, имеют одинаковый набор топологических порядков.

Комбинаторное перечисление

В перечисление графов задача подсчета ориентированных ациклических графов изучалась Робинсон (1973).[11]Количество DAG на п помеченные вершины, для п = 0, 1, 2, 3, … (без ограничений на порядок, в котором эти номера появляются в топологическом порядке DAG)

1, 1, 3, 25, 543, 29281, 3781503,… (последовательность A003024 в OEIS).

Эти числа могут быть вычислены отношение повторения

[11]

Эрик В. Вайсштейн предположил,[12] и McKay et al. (2004) доказано, что одни и те же числа считают (0,1) матрицы для чего все собственные значения положительные действительные числа. Доказательство биективный: матрица А является матрица смежности DAG тогда и только тогда, когда А + я является (0,1) -матрицей со всеми положительными собственными значениями, где я обозначает единичная матрица. Потому что DAG не может иметь петли, его матрица смежности должна иметь нулевую диагональ, поэтому добавляя я сохраняет свойство, что все коэффициенты матрицы равны 0 или 1.[13]

Связанные семейства графов

А многодерево, группа DAG, образованная ориентирование края неориентированного дерева
А многодерево, DAG, в котором каждый подграф, достижимый из одной вершины (красный), является деревом

А многодерево ориентированный граф, образованный ориентацией ребер бесплатное дерево.[14] Каждое многодерево - это DAG. В частности, это касается древесные растения формируется путем направления всех краев наружу от корней дерева.

А многодерево (также называемый строго однозначным графом или мангровым лесом) - ориентированный граф, в котором существует не более одного направленного пути (в любом направлении) между любыми двумя вершинами; эквивалентно, это DAG, в котором для каждой вершины v, подграф достижимый из v образует дерево.[15]

Вычислительные проблемы

Топологическая сортировка и распознавание

Основная статья: Топологическая сортировка

Топологическая сортировка алгоритмическая проблема нахождения топологического упорядочения данного DAG. Это можно решить в линейное время.[16] Алгоритм топологической сортировки Кана строит порядок вершин напрямую. Он поддерживает список вершин, у которых нет входящих ребер из других вершин, которые еще не были включены в частично построенный топологический порядок; изначально этот список состоит из вершин без входящих ребер. Затем он несколько раз добавляет одну вершину из этого списка в конец частично построенного топологического упорядочения и проверяет, должны ли ее соседи быть добавлены в список. Алгоритм завершается, когда все вершины обработаны таким образом.[17] В качестве альтернативы топологический порядок может быть построен путем обращения почтовый заказ нумерация поиск в глубину обход графа.[16]

Также можно проверить, является ли данный ориентированный граф DAG за линейное время, либо попытавшись найти топологическое упорядочение, а затем проверив для каждого ребра, действителен ли полученный порядок.[18] или, альтернативно, для некоторых алгоритмов топологической сортировки, путем проверки того, что алгоритм успешно упорядочивает все вершины без выполнения условия ошибки.[17]

Построение из циклических графов

Любой неориентированный граф можно превратить в DAG, выбрав общий заказ для его вершин и направляя каждое ребро от более ранней конечной точки в порядке к более поздней конечной точке. Результирующий ориентация ребер называется ациклическая ориентация. Различные общие порядки могут привести к одной и той же ациклической ориентации, поэтому п-вершинный граф может иметь меньше чем п! ациклические ориентации. Количество ациклических ориентаций равно |χ(−1)|, куда χ это хроматический полином данного графа.[19]

Желтый ориентированный ациклический граф - это конденсация синего ориентированного графа. Он образован договор каждый компонент сильной связности синего графа в одну желтую вершину.

Любой ориентированный граф можно превратить в DAG, удалив набор вершин обратной связи или набор дуги обратной связи, набор вершин или ребер (соответственно), который касается всех циклов. Однако наименьший такой набор NP-жесткий найти.[20] Произвольный ориентированный граф также может быть преобразован в DAG, называемый его конденсация, к договор каждый из его компоненты сильной связности в единую супервершину.[21] Когда граф уже является ациклическим, его наименьшие наборы вершин обратной связи и наборы дуг обратной связи равны пустой, а его уплотнение - это сам граф.

Переходное замыкание и переходное сокращение

Транзитивное закрытие данного DAG с п вершины и м ребра, могут быть построены во времени О(млн) используя либо поиск в ширину или поиск в глубину для проверки достижимости из каждой вершины.[22] Как вариант, ее можно решить вовремя О(пω) куда ω < 2.373 показатель для алгоритмы быстрого матричного умножения; это теоретическое улучшение по сравнению с О(млн) граница для плотные графы.[23]

Во всех этих алгоритмах транзитивного замыкания можно отличать пары вершин, которые достижимы по крайней мере одним путем длиной два или более, от пар, которые могут быть соединены только путем длины один. Транзитивная редукция состоит из ребер, которые образуют пути длиной один, которые являются единственными путями, соединяющими их конечные точки. Следовательно, транзитивная редукция может быть построена в тех же асимптотических временных рамках, что и транзитивное замыкание.[24]

Проблема закрытия

Основная статья: Проблема закрытия

В проблема закрытия принимает на вход ориентированный ациклический граф, взвешенный по вершинам, и ищет минимальный (или максимальный) вес замыкания - набор вершин C, такие, что никакие края не выходят C. Задача может быть сформулирована для ориентированных графов без предположения об ацикличности, но без большей общности, поскольку в этом случае она эквивалентна той же задаче о сгущении графа. Ее можно решить за полиномиальное время, используя редукцию к проблема максимального расхода.[25]

Алгоритмы пути

Некоторые алгоритмы упрощаются при использовании в группах DAG вместо общих графов, основанных на принципе топологического упорядочения. Например, можно найти кратчайшие пути и самые длинные пути от заданной начальной вершины в DAG за линейное время путем обработки вершин в топологическом порядке и вычисления длины пути для каждой вершины как минимальной или максимальной длины, полученной через любое из входящих в нее ребер.[26] Напротив, для произвольных графов кратчайший путь может потребовать более медленных алгоритмов, таких как Алгоритм Дейкстры или Алгоритм Беллмана – Форда,[27] а самые длинные пути в произвольных графах равны NP-жесткий найти.[28]

Приложения

Планирование

Направленные ациклические графы-представления частичных порядков имеют множество приложений в планирование для систем задач с упорядочивающими ограничениями.[29]Важный класс проблем этого типа касается коллекций объектов, которые необходимо обновить, таких как ячейки электронная таблица после смены одной из ячеек или объектные файлы компьютерного программного обеспечения после его исходный код был изменен. В этом контексте граф зависимостей представляет собой граф, имеющий вершину для каждого обновляемого объекта и ребро, соединяющее два объекта, когда один из них необходимо обновить раньше, чем другой. Цикл в этом графе называется круговая зависимость, и обычно не допускается, потому что не было бы возможности согласованно планировать задачи, участвующие в цикле. Графы зависимостей без циклических зависимостей образуют группы DAG.[30]

Например, когда одна ячейка электронная таблица изменений, необходимо пересчитать значения других ячеек, которые прямо или косвенно зависят от измененной ячейки. Для этой проблемы задачи, которые должны быть запланированы, - это пересчет значений отдельных ячеек электронной таблицы. Зависимости возникают, когда выражение в одной ячейке использует значение из другой ячейки. В таком случае используемое значение должно быть пересчитано раньше, чем выражение, которое его использует. Топологическое упорядочение графа зависимостей и использование этого топологического порядка для планирования обновлений ячеек позволяет обновлять всю электронную таблицу с помощью только одной оценки для каждой ячейки.[31] Подобные проблемы с упорядочением задач возникают в make-файлы для компиляции программы[31] и планирование инструкций для низкоуровневой оптимизации компьютерных программ.[32]

Диаграмма PERT для проекта с пятью вехами (обозначенными 10–50) и шестью задачами (обозначенными A – F). Есть два критических пути: ADF и BC.

Несколько иную формулировку ограничений планирования на основе DAG использует методика оценки и обзора программ (PERT), метод управления крупными человеческими проектами, который был одним из первых приложений DAG. В этом методе вершины группы DAG представляют вехи проекта, а не конкретных задач, которые необходимо выполнить. Вместо этого задача или действие представлены краем группы доступности базы данных, соединяющей две вехи, которые отмечают начало и завершение задачи. Каждое такое ребро помечено приблизительным количеством времени, которое потребуется команде рабочих для выполнения задачи. В самый длинный путь в этом DAG представляет критический путь проекта, тот, который контролирует общее время проекта. Отдельные этапы можно запланировать в соответствии с длинами самых длинных путей, заканчивающихся в их вершинах.[33]

Сети обработки данных

Направленный ациклический граф может использоваться для представления сети обрабатывающих элементов. В этом представлении данные поступают в обрабатывающий элемент через его входящие края и покидают элемент через его исходящие края.

Например, в конструкции электронных схем статический комбинационная логика блоки можно представить как ациклическую систему логические ворота который вычисляет функцию входа, где вход и выход функции представлены как отдельные биты. Как правило, выходные данные этих блоков не могут использоваться в качестве входных, если они не захватываются регистром или элементом состояния, который сохраняет свои ациклические свойства.[34] Электронные схемы на бумаге или в базе данных представляют собой форму ориентированных ациклических графов, использующих экземпляры или компоненты для формирования направленной ссылки на компонент более низкого уровня. Сами по себе электронные схемы не обязательно являются ациклическими или направленными.

Программирование потока данных языки описывают системы операций над потоки данных, и связи между выходами одних операций и входами других. Эти языки могут быть удобны для описания повторяющихся задач обработки данных, в которых один и тот же ациклически связанный набор операций применяется ко многим элементам данных. Они могут быть выполнены как параллельный алгоритм в котором каждая операция выполняется параллельным процессом, как только ему становится доступен другой набор входных данных.[35]

В компиляторы, прямой код (то есть последовательности операторов без циклов или условных ветвей) может быть представлен DAG, описывающим входы и выходы каждой из арифметических операций, выполняемых в коде. Это представление позволяет компилятору выполнять исключение общего подвыражения эффективно.[36] На более высоком уровне организации кода принцип ациклических зависимостей утверждает, что зависимости между модулями или компонентами большой программной системы должны образовывать направленный ациклический граф.[37]

Причинные структуры

Основная статья: Байесовская сеть

Графы, в которых вершины представляют события, происходящие в определенное время, и где ребра всегда являются точкой от вершины раннего времени до вершины ребра позднего времени, обязательно являются направленными и ациклическими. Отсутствие цикла следует из-за того, что время, связанное с вершиной, всегда увеличивается, когда вы следуете за любым дорожка в графе, поэтому вы никогда не сможете вернуться к вершине на пути. Это отражает нашу естественную интуицию, что причинность означает, что события могут влиять только на будущее, они никогда не влияют на прошлое, и, следовательно, у нас нет причинные петли. Примером этого типа ориентированного ациклического графа являются графы, встречающиеся в причинно-следственный подход к квантовой гравитации хотя в этом случае рассматриваемые графики транзитивно полный. В примере с историей версий каждая версия программного обеспечения связана с уникальным временем, обычно со временем, когда версия была сохранена, зафиксирована или выпущена. Для диаграмм цитирования документы публикуются одновременно и могут относиться только к более старым документам.

Иногда события не связаны с конкретным физическим временем. При условии, что пары событий имеют чисто причинную связь, то есть ребра представляют причинно-следственные связи между событиями у нас будет ориентированный ациклический граф.[38] Например, Байесовская сеть представляет систему вероятностных событий в виде вершин в ориентированном ациклическом графе, в котором вероятность события может быть вычислена из вероятностей его предшественников в группе DAG.[39] В этом контексте моральный граф DAG - это неориентированный граф, созданный путем добавления (неориентированного) ребра между всеми родителями одной и той же вершины (иногда называемого жениться), а затем заменяя все направленные ребра неориентированными ребрами.[40] Другой тип графа с похожей причинной структурой - это диаграмма влияния, вершины которого представляют либо решения, которые необходимо принять, либо неизвестную информацию, а ребра представляют собой причинные влияния от одной вершины к другой.[41] В эпидемиологиянапример, эти диаграммы часто используются для оценки ожидаемой ценности различных вариантов вмешательства.[42][43]

Обратное также верно. То есть в любом приложении, представленном ориентированным ациклическим графом, существует причинная структура, либо явный порядок, либо время в примере, либо порядок, который может быть получен из структуры графа. Это следует потому, что все ориентированные ациклические графы имеют топологический порядок, т.е. есть хотя бы один способ разместить вершины в таком порядке, чтобы все ребра указывали в одном направлении в этом порядке.

Генеалогия и история версий

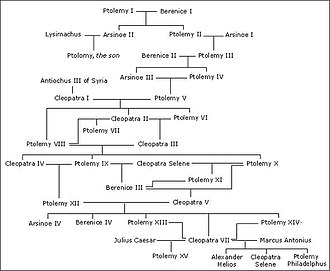
Генеалогическое древо Династия птолемеев, со многими браками между близкие родственники вызывая коллапс родословной

Семейные деревья можно рассматривать как ориентированные ациклические графы с вершиной для каждого члена семьи и ребром для каждого отношения родитель-потомок.[44] Несмотря на название, эти графы не обязательно являются деревьями из-за возможности браков между родственниками (таким образом, у ребенка есть общий предок как со стороны матери, так и со стороны отца), что приводит к коллапс родословной.[45] Графики по материнской линии по происхождению ("материнские" отношения между женщинами) и патрилинейный происхождение («отцовские» отношения между мужчинами) - это деревья внутри этого графа. Поскольку никто не может стать своим собственным предком, генеалогические деревья ацикличны.[46]

По той же причине история версий распределенный контроль версий система, такая как Git,[47] обычно имеет структуру ориентированного ациклического графа, в котором есть вершина для каждой ревизии и ребро, соединяющее пары ревизий, которые были напрямую получены друг из друга. Это вообще не деревья из-за слияний.[48]

Во многих рандомизированный алгоритмы в вычислительная геометрия, алгоритм поддерживает история DAG представляет историю версий геометрической конструкции в ходе последовательности изменений конструкции. Например, в рандомизированный инкрементальный алгоритм для Триангуляция Делоне, триангуляция изменяется путем замены одного треугольника тремя меньшими треугольниками при добавлении каждой точки и операциями «переворота», при которых пары треугольников заменяются другой парой треугольников. DAG истории для этого алгоритма имеет вершину для каждого треугольника, построенного как часть алгоритма, и ребра от каждого треугольника до двух или трех других треугольников, которые его заменяют. Эта структура позволяет точка расположения запросы, на которые нужно эффективно отвечать: найти местоположение точки запроса q в триангуляции Делоне проследуйте путь в истории DAG, на каждом шаге переходя к треугольнику замены, который содержит q. Последний треугольник, достигнутый на этом пути, должен быть треугольником Делоне, который содержит q.[49]

Графики цитирования

В график цитирования вершины - документы с единой датой публикации. Края представляют собой ссылки из библиографии одного документа на другие, обязательно более ранние документы. Классический пример - это цитаты между академическими статьями, как указано в статье 1965 года «Сети научных статей».[50] к Дерек Дж. Де Солла Прайс кто создал первую модель сети цитирования, Ценовая модель.[51] В этом случае количество цитирований статьи - это просто входящая степень соответствующей вершины сети цитирования. Это важная мера в анализ цитирования. Судебные решения приведите другой пример, поскольку судьи подтверждают свои выводы по одному делу, ссылаясь на другие решения, принятые ранее по предыдущим делам. Последний пример - патенты, которые должны быть упомянуты ранее. предшествующий уровень техники, более ранние патенты, которые имеют отношение к текущей заявке на патент. Принимая во внимание особые свойства направленных ациклических графов, можно анализировать сети цитирования с помощью методов, недоступных при анализе общих графов, рассматриваемых во многих исследованиях, с использованием сетевой анализ. Например переходная редукция дает новое представление о распределении цитирования в различных приложениях, подчеркивая явные различия в механизмах создания сетей цитирования в разных контекстах.[52] Другая техника анализ основного пути, который отслеживает ссылки цитирования и предлагает наиболее важные цепочки цитирования в данной график цитирования.

В Ценовая модель слишком прост, чтобы быть реалистичной моделью сеть цитирования но это достаточно просто, чтобы учесть аналитические решения для некоторых из его свойств. Многие из них можно найти, используя результаты, полученные из неориентированной версии Ценовая модель, то Модель Барабаши – Альберта. Однако, поскольку Модель цены дает ориентированный ациклический граф, это полезная модель при поиске аналитических вычислений свойств, уникальных для ориентированных ациклических графов. Например, длина самого длинного пути от n-го узла, добавленного в сеть, до первого узла в сети, масштабируется как[53] .

Сжатие данных

Направленные ациклические графы можно также использовать как компактное представление коллекции последовательностей. В приложении этого типа можно найти группу DAG, в которой пути образуют заданные последовательности. Когда многие из последовательностей совместно используют одни и те же подпоследовательности, эти общие подпоследовательности могут быть представлены общей частью DAG, что позволяет представлению использовать меньше места, чем для перечисления всех последовательностей по отдельности. Например, направленный ациклический граф слов это структура данных в информатике - ориентированный ациклический граф с одним источником и ребра, помеченные буквами или символами; пути от источника к стокам на этом графике представляют собой набор струны, например, английские слова.[54] Любой набор последовательностей может быть представлен как пути в дереве, сформировав вершину дерева для каждого префикса последовательности и сделав родительский элемент одной из этих вершин представлением последовательности с одним меньшим элементом; сформированное таким образом дерево для набора строк называется три. Направленный ациклический граф слов экономит место в дереве, позволяя путям расходиться и объединяться, так что набор слов с одинаковыми возможными суффиксами может быть представлен одной вершиной дерева.[55]

Та же идея использования группы доступности базы данных для представления семейства путей встречается в диаграмма двоичных решений,[56][57] структура данных на основе DAG для представления двоичных функций. На диаграмме бинарных решений каждая вершина, не являющаяся приемником, помечена именем двоичной переменной, а каждый приемник и каждое ребро помечены цифрами 0 или 1. Значение функции для любого назначение истины к переменным - это значение в приемнике, найденное путем следования пути, начиная с единственной исходной вершины, который в каждой вершине, не являющейся приемником, следует за исходящим ребром, помеченным значением переменной этой вершины. Подобно тому, как ориентированные ациклические графы слов можно рассматривать как сжатую форму попыток, диаграммы бинарных решений можно рассматривать как сжатые формы деревья решений которые экономят место, позволяя путям воссоединяться, когда они согласовывают результаты всех оставшихся решений.[58]

Рекомендации

  1. ^ а б Thulasiraman, K .; Свами, М. Н. С. (1992), "5.7 Ациклические ориентированные графы", Графики: теория и алгоритмы, Джон Вили и сын, стр. 118, ISBN 978-0-471-51356-8.
  2. ^ а б c Банг-Дженсен, Йорген (2008), «2.1 Ациклические диграфы», Орграфы: теория, алгоритмы и приложения, Springer Monographs in Mathematics (2-е изд.), Springer-Verlag, стр. 32–34, ISBN 978-1-84800-997-4.
  3. ^ Христофидес, Никос (1975), Теория графов: алгоритмический подход, Academic Press, стр. 170–174..
  4. ^ Митрани, И. (1982), Методы моделирования для дискретных систем событий, Cambridge Computer Science Texts, 14, Cambridge University Press, стр. 27, ISBN 9780521282826.
  5. ^ Козен, Декстер (1992), Дизайн и анализ алгоритмов, Монографии по информатике, Springer, стр. 9, ISBN 978-0-387-97687-7.
  6. ^ Банерджи, Утпал (1993), «Упражнение 2 (с)», Циклические преобразования для реструктуризации компиляторов: основы, Springer, стр. 19, ISBN 978-0-7923-9318-4.
  7. ^ Банг-Йенсен, Йорген; Гутин, Грегори З. (2008), "2.3 Транзитивные орграфы, транзитивные замыкания и редукции", Орграфы: теория, алгоритмы и приложения, Монографии Springer по математике, Springer, стр. 36–39, ISBN 978-1-84800-998-1.
  8. ^ Юнгникель, Дитер (2012), Графики, сети и алгоритмы, Алгоритмы и вычисления в математике, 5, Springer, стр. 92–93, ISBN 978-3-642-32278-5.
  9. ^ Седжвик, Роберт; Уэйн, Кевин (2011), «4,2,25 Уникальный топологический порядок», Алгоритмы (4-е изд.), Addison-Wesley, стр. 598–599, ISBN 978-0-13-276256-4.
  10. ^ Бендер, Эдвард А .; Уильямсон, С. Гилл (2005), «Пример 26 (Линейные расширения - топологические виды)», Краткий курс дискретной математики, Dover Books on Computer Science, Courier Dover Publications, p. 142, ISBN 978-0-486-43946-4.
  11. ^ а б Робинсон, Р. В. (1973), "Подсчет помеченных ациклических диграфов", в Харари, Ф. (ред.), Новые направления в теории графов, Academic Press, стр. 239–273.. Смотрите также Харари, Фрэнк; Палмер, Эдгар М. (1973), Графическое перечисление, Академическая пресса, п. 19, ISBN 978-0-12-324245-7.
  12. ^ Вайсштейн, Эрик В., "Гипотеза Вайсштейна", MathWorld
  13. ^ Маккей, Б.Д.; Ройл, Г.Ф.; Wanless, I. M .; Огье, Ф.; Слоан, Н. Дж. А.; Уилф, Х. (2004), «Ациклические орграфы и собственные значения (0,1) -матриц», Журнал целочисленных последовательностей, 7, Статья 04.3.3.
  14. ^ Ребане, Джордж; Жемчужина, Иудея (1987), «Восстановление причинных поли-деревьев из статистических данных», в Proc. 3-я ежегодная конференция по неопределенности в искусственном интеллекте (UAI 1987), Сиэтл, Вашингтон, США, июль 1987 г. (PDF), стр. 222–228[постоянная мертвая ссылка].
  15. ^ Фурнаш, Джордж У.; Закс, Джефф (1994), «Многодеревья: обогащение и повторное использование иерархической структуры», Proc. Конференция SIGCHI по человеческому фактору в вычислительных системах (CHI '94), стр. 330–336, Дои:10.1145/191666.191778, ISBN 978-0897916509, S2CID 18710118.
  16. ^ а б Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001) [1990], Введение в алгоритмы (2-е изд.), MIT Press и McGraw-Hill, ISBN 0-262-03293-7 Раздел 22.4, Топологическая сортировка, стр. 549–552.
  17. ^ а б Юнгникель (2012)С. 50–51.
  18. ^ За поиск в глубину основанный на алгоритме топологической сортировки, эта проверка достоверности может чередоваться с самим алгоритмом топологической сортировки; см. например Скиена, Стивен С. (2009), Руководство по разработке алгоритмов, Springer, стр. 179–181, ISBN 978-1-84800-070-4.
  19. ^ Стэнли, Ричард П. (1973), «Ациклические ориентации графов» (PDF), Дискретная математика, 5 (2): 171–178, Дои:10.1016 / 0012-365X (73) 90108-8.
  20. ^ Гарей, Майкл Р.; Джонсон, Дэвид С. (1979), Компьютеры и непреодолимость: руководство по теории NP-полноты, В. Х. Фриман, ISBN 0-7167-1045-5, Проблемы GT7 и GT8, стр. 191–192.
  21. ^ Харари, Фрэнк; Норман, Роберт З .; Картрайт, Дорвин (1965), Структурные модели: введение в теорию ориентированных графов, John Wiley & Sons, стр. 63.
  22. ^ Скиена (2009), п. 495.
  23. ^ Скиена (2009), п. 496.
  24. ^ Банг-Дженсен и Гутин (2008), п. 38.
  25. ^ Пикар, Жан-Клод (1976), "Максимальное замыкание графа и приложения к комбинаторным задачам", Наука управления, 22 (11): 1268–1272, Дои:10.1287 / mnsc.22.11.1268, Г-Н 0403596.
  26. ^ Cormen et al. 2001, раздел 24.2, Кратчайшие пути из одного источника в ориентированных ациклических графах, стр. 592–595.
  27. ^ Cormen et al. 2001, разделы 24.1, Алгоритм Беллмана – Форда, стр. 588–592, и 24.3, Алгоритм Дейкстры, стр. 595–601.
  28. ^ Cormen et al. 2001, стр. 966.
  29. ^ Скиена (2009), п. 469.
  30. ^ Al-Mutawa, H.A .; Дитрих, Дж .; Marsland, S .; Маккартин, К. (2014), "О форме круговых зависимостей в программах Java", 23-я Австралийская конференция по разработке программного обеспечения, IEEE, стр. 48–57, Дои:10.1109 / ASWEC.2014.15, ISBN 978-1-4799-3149-1, S2CID 17570052.
  31. ^ а б Гросс, Джонатан Л .; Йеллен, Джей; Чжан, Пин (2013), Справочник по теории графов (2-е изд.), CRC Press, стр. 1181, г. ISBN 978-1-4398-8018-0.
  32. ^ Срикант, Ю.Н. Шанкар, Прити (2007), Справочник по проектированию компиляторов: оптимизация и создание машинного кода (2-е изд.), CRC Press, стр. 19–39, ISBN 978-1-4200-4383-9.
  33. ^ Ван, Джон X. (2002), Что должен знать каждый инженер о принятии решений в условиях неопределенности, CRC Press, стр. 160, ISBN 978-0-8247-4373-4.
  34. ^ Сапатнекар, Сачин (2004), Время, Springer, стр. 133, ISBN 978-1-4020-7671-8.
  35. ^ Деннис, Джек Б. (1974), "Первая версия языка процедур потока данных", Симпозиум по программированию, Конспект лекций по информатике, 19, стр. 362–376, Дои:10.1007/3-540-06859-7_145, ISBN 978-3-540-06859-4.
  36. ^ Туати, Сид; де Динешин, Бенуа (2014), Расширенная оптимизация серверной части, John Wiley & Sons, стр. 123, ISBN 978-1-118-64894-0.
  37. ^ Гарланд, Джефф; Энтони, Ричард (2003), Крупномасштабная программная архитектура: практическое руководство с использованием UML, John Wiley & Sons, стр. 215, ISBN 9780470856383.
  38. ^ Гопник, Элисон; Шульц, Лаура (2007), Причинное обучение, Oxford University Press, стр. 4, ISBN 978-0-19-803928-0.
  39. ^ Шмулевич, Илья; Догерти, Эдвард Р. (2010), Вероятностные булевы сети: моделирование и контроль регуляторных сетей генов, Общество промышленной и прикладной математики, стр. 58, ISBN 978-0-89871-692-4.
  40. ^ Коуэлл, Роберт Дж .; Давид, А. Филип; Лауритцен, Штеффен Л.; Шпигельхальтер, Дэвид Дж. (1999), «3.2.1 Морализация», Вероятностные сети и экспертные системы, Springer, стр. 31–33, ISBN 978-0-387-98767-5.
  41. ^ Дорф, Ричард К. (1998), Справочник по управлению технологиями, CRC Press, стр. 9-7, ISBN 978-0-8493-8577-3.
  42. ^ Босло, Сара (2008), Энциклопедия эпидемиологии, том 1, Шалфей, стр. 255, ISBN 978-1-4129-2816-8.
  43. ^ Перл, Иудея (1995), «Причинные диаграммы для эмпирических исследований», Биометрика, 82 (4): 669–709, Дои:10.1093 / biomet / 82.4.669.
  44. ^ Киркпатрик, Бонни Б. (апрель 2011 г.), "Гаплотипы против генотипов в родословных", Алгоритмы молекулярной биологии, 6 (10): 10, Дои:10.1186/1748-7188-6-10, ЧВК 3102622, PMID 21504603.
  45. ^ McGuffin, M.J .; Балакришнан, Р. (2005), «Интерактивная визуализация генеалогических графиков» (PDF), Симпозиум IEEE по визуализации информации (INFOVIS 2005), стр. 16–23, Дои:10.1109 / INFVIS.2005.1532124, ISBN 978-0-7803-9464-3.
  46. ^ Бендер, Майкл А .; Пеммасани, Гиридхар; Скиена, Стивен; Сумазин, Павел (2001), «Поиск наименее общих предков в ориентированных ациклических графах», Материалы двенадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '01), Филадельфия, Пенсильвания, США: Общество промышленной и прикладной математики, стр. 845–854, ISBN 978-0-89871-490-6.
  47. ^ "gitglossary Documentation". Git. Сохранение свободы программного обеспечения. Получено 7 ноября 2020.
  48. ^ Бартланг, Удо (2010), Архитектура и методы гибкого управления контентом в одноранговых системах, Springer, стр. 59, ISBN 978-3-8348-9645-2.
  49. ^ Пах, Янош; Шарир, Миха, Комбинаторная геометрия и ее алгоритмические приложения: лекции по Алкале, Математические обзоры и монографии, 152, Американское математическое общество, стр. 93–94, ISBN 978-0-8218-7533-9.
  50. ^ Прайс, Дерек Дж. Де Солла (30 июля 1965 г.), "Сети научных публикаций" (PDF), Наука, 149 (3683): 510–515, Bibcode:1965Научный ... 149..510D, Дои:10.1126 / science.149.3683.510, PMID 14325149.
  51. ^ Прайс, Дерек Дж. Де Солла (1976), «Общая теория библиометрических и других процессов накопления преимуществ», J.Amer.Soc.Inform.Sci., 27: 292–306, Дои:10.1002 / asi.4630270505.
  52. ^ Клаф, Джеймс Р .; Голлингс, Джейми; Вьюн, Тамар В .; Эванс, Тим С. (2015), "Переходное сокращение сетей цитирования", Журнал сложных сетей, 3 (2): 189–203, arXiv:1310.8224, Дои:10.1093 / comnet / cnu039, S2CID 10228152.
  53. ^ Evans, T.S .; Calmon, L .; Василяускайте, В. (2020), «Самый длинный путь в ценовой модели», Научные отчеты, 10 (1): 10503, arXiv:1903.03667, Bibcode:2020НатСР..1010503Е, Дои:10.1038 / s41598-020-67421-8, ЧВК 7324613, PMID 32601403
  54. ^ Крошмор, Максим; Верен, Рено (1997), "Прямое построение компактных ориентированных ациклических графов слов", Комбинаторное сопоставление с образцом, Конспект лекций по информатике, 1264, Springer, стр. 116–129, CiteSeerX 10.1.1.53.6273, Дои:10.1007/3-540-63220-4_55, ISBN 978-3-540-63220-7.
  55. ^ Лотэр, М. (2005), Прикладная комбинаторика слов, Энциклопедия математики и ее приложений, 105, Cambridge University Press, стр. 18, ISBN 9780521848022.
  56. ^ Ли, К. Я. (1959), "Представление коммутационных схем программами с двоичным решением", Технический журнал Bell System, 38 (4): 985–999, Дои:10.1002 / j.1538-7305.1959.tb01585.x.
  57. ^ Акерс, Шелдон Б. (1978), "Диаграммы двоичных решений", Транзакции IEEE на компьютерах, С-27 (6): 509–516, Дои:10.1109 / TC.1978.1675141, S2CID 21028055.
  58. ^ Friedman, S.J .; Суповит, К. Дж. (1987), "Нахождение оптимального порядка переменных для диаграмм двоичных решений", Proc. 24-я конференция ACM / IEEE по автоматизации проектирования (DAC '87), Нью-Йорк, Нью-Йорк, США: ACM, стр. 348–356, Дои:10.1145/37888.37941, ISBN 978-0-8186-0781-3, S2CID 14796451.

внешняя ссылка