WikiDer > Электронная оптика

Electron optics
Магнитная линза

Электронная оптика математическая основа для расчета траекторий электронов вдоль электромагнитные поля. Период, термин оптика используется потому что магнитный и электростатический линзы действуют на пучок заряженных частиц аналогично оптические линзы на световой луч.

Расчеты электронной оптики имеют решающее значение для проектирования электронные микроскопы и ускорители частиц. в параксиальное приближение, траекторные расчеты могут быть выполнены с использованием матричный анализ переноса лучей.

An линза einzel, особый тип электростатической линзы. На этом рисунке показан путь электрона. Шесть пластин параллельны траектории полета, а средняя пластина находится под определенным потенциалом. (Эта диаграмма была сделана для положительных ионов и показывает положительное напряжение на центральной пластине. Для электронов это напряжение должно быть отрицательным.)

Электронные свойства

Основная статья: Электрон

Электроны - это заряженные частицы (точечные сборы с масса покоя) с вращение 1/2 (следовательно, они фермионы). Электроны могут быть ускоренный подходящим электрический (или же магнитный) полей, тем самым получая кинетическая энергия. При достаточном напряжении электрон может быть ускорен достаточно быстро, чтобы показать измеримый релятивистские эффекты. В соответствии с дуальность волновых частиц, электроны также можно рассматривать как волны материи с такими свойствами, как длина волны, фаза и амплитуда.

Геометрическая электронная оптика

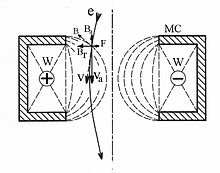
Магнитные поля

Электроны взаимодействуют с магнитными полями согласно второму члену силы Лоренца: a перекрестное произведение между магнитным полем и скоростью электронов. В бесконечном однородном поле это приводит к круговое движение электрона вокруг направления поля с радиусом, определяемым как:

куда р - радиус орбиты, м это масса электрона, - компонента скорости электрона, перпендикулярная полю, е - заряд электрона и B - величина приложенного магнитного поля. Электроны, у которых есть компонента скорости, параллельная магнитному полю, будут двигаться вдоль спиральный траектории.

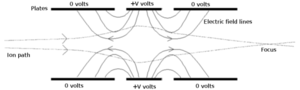
Электрические поля

В случае приложения электростатического поля электрон будет отклоняться в сторону положительного градиента поля. Примечательно, что это пересечение силовых линий электростатического поля означает, что электроны, перемещаясь через электростатические поля, изменяют величину своей скорости, тогда как в магнитных полях изменяется только направление скорости.

Поскольку электроны могут проявлять нечастичные (волновые) эффекты, такие как дифракция, полный анализ путей электронов можно получить, решив Уравнение Максвелла- однако во многих ситуациях интерпретация частиц может обеспечить достаточное приближение с большим уменьшением сложности.

Еще одно свойство электронов состоит в том, что они сильно взаимодействуют с веществом, поскольку они чувствительны не только к ядру, но и к облаку электронных зарядов вещества. Следовательно, электроны требуют вакуум распространяться на любое разумное расстояние, например, желаемое в электронно-оптической системе.

Проникновение в вакуум продиктовано длина свободного пробега, мера вероятности столкновения электронов с веществом, приблизительные значения для которой могут быть получены из Статистика Пуассона.

Квантовая теория

Хотя это не очень распространено, также возможно получить эффекты магнитных структур для заряженных частиц, начиная с Уравнение Дирака.[1]

Дифракционная электронная оптика

Субрелятивистский свободный электрон, распространяющийся в вакуум можно точно описать как де Бройль волна материи с длиной волны, обратно пропорциональной его продольному импульсу. В результате наличия заряда, переносимого электроном, электрические поля, магнитные поля или средний электростатический внутренний потенциал тонких, слабо взаимодействующих материалов могут придавать фазовый сдвиг волновому фронту электрона.[2] С модуляцией по толщине нитрид кремния мембраны и устройства с программируемым фазовым сдвигом использовали эти свойства для применения пространственно изменяющихся фазовых сдвигов для управления пространственной интенсивностью и фазой электронной волны в дальней зоне. Подобные устройства применялись для произвольной формы электронного волнового фронта, исправления аберрации присущий электронные микроскопы, разрешите орбитальный угловой момент свободного электрона, и измерить дихроизм при взаимодействии свободных электронов с магнитными материалами или плазмонными наноструктурами.[3]

Смотрите также

дальнейшее чтение

  • Хоукс, П. В. и Каспер, Э. (1994). Принципы электронной оптики. Академическая пресса. ISBN 9780080984162.
  • Поцци, Г. (2016). Частицы и волны в электронной оптике и микроскопии. Академическая пресса. ISBN 9780128048146.

Рекомендации

  1. ^ Джаганнатан, Р.; Саймон, Р.; Сударшан, Э.; Мукунда, Н. (1989). «Квантовая теория магнитных электронных линз на основе уравнения Дирака» (PDF). Письма о физике A. 134 (8–9): 457. Bibcode:1989PhLA..134..457J. Дои:10.1016/0375-9601(89)90685-3.
  2. ^ Поцци, Джулио; Питер Хоукс (2016). «Частицы и волны в электронной оптике и микроскопии». Достижения в области визуализации и электронной физики. 194 (2): 1–336. Дои:10.1016 / bs.aiep.2016.02.001.
  3. ^ Шайло, Рой; Лу, Пэн-Хан; Ремез, Рой; Таваби, Амир Х.; Поцци, Джулио; Дунин-Борковски, Рафал Э; Арье, Ади (2019). «Наноструктурирование электронных пучков». Physica Scripta. 94 (3): 034004. Bibcode:ФОТО 2019 ... 94c4004S. Дои:10.1088 / 1402-4896 / aaf258. ISSN 0031-8949.