WikiDer > Спираль
А спираль (/ˈчасялɪks/), множественное число спирали или спирали (/ˈчасɛлɪsяz/), представляет собой форму штопора или винтовой лестницы. Это тип гладкий; плавный пространственная кривая с касательные линии на постоянном угол к фиксированной оси. Спирали важны в биология, как ДНК молекула образуется как две переплетенные спирали, и много белки имеют винтовые подструктуры, известные как альфа спирали. Слово спираль исходит из Греческий слово ἕλιξ, "закрученный, изогнутый".[1] «Заливная» спираль - например, «спиральный» (винтовой) наклонный участок - называется геликоид.[2]
Типы
Спирали могут быть правосторонними или левосторонними. Если при взгляде вдоль оси спирали вращательное движение по часовой стрелке отодвигает спираль от наблюдателя, то это называется правой спиралью; если в сторону наблюдателя, то это левая спираль. Ручка (или хиральность) является свойством спирали, а не перспективы: правую спираль нельзя повернуть так, чтобы она выглядела как левосторонняя, если ее не смотреть в зеркало, и наоборот.

Большинство оборудования винтовая резьба - правые спирали. Альфа-спираль в биологии, а также А и B формы ДНК также являются правыми спиралями. В Z форма ДНК левша.
В подача спирали - это высота одного полного витка спирали, измеренная параллельно оси спирали.
А двойная спираль состоит из двух (обычно конгруэнтный) спирали с одинаковой осью, отличающиеся перемещением вдоль оси.[3]
А коническая спираль можно определить как спираль на конической поверхности, при этом расстояние до вершины экспоненциально зависит от угла, указывающего направление от оси. Примером может служить Штопор американские горки на Cedar Point парк культуры и отдыха.
А круговая спираль, (т.е. один с постоянным радиусом) имеет постоянную полосу кривизна и постоянный кручение.
Кривая называется общая спираль или цилиндрическая спираль[4] если его касательная составляет постоянный угол с фиксированной линией в пространстве. Кривая является общей спиралью тогда и только тогда, когда отношение кривизна к кручение постоянно.[5]
Геометрический шаг - это расстояние, на которое элемент воздушного винта продвинулся бы за один оборот, если бы он двигался по спирали, имеющей угол, равный углу между хордой элемента и плоскостью, перпендикулярной оси винта.
Кривая называется наклонная спираль если его главная нормаль образует постоянный угол с фиксированной линией в пространстве.[6] Его можно построить, применив преобразование к подвижной системе отсчета общей спирали.[7]
Некоторые кривые, встречающиеся в природе, состоят из множества спиралей разной направленности, соединенных переходами, известными как усики извращения.
Математическое описание
В математика, спираль - это изгиб в 3-размерный Космос. Следующее параметризация в Декартовы координаты определяет конкретную спираль;[8] возможно, самое простое уравнение для одного -
Поскольку параметр т увеличивается, точка (Икс(т),у(т),z(т)) прослеживает правую спираль шага 2π (или наклон 1) и радиус 1 относительно z-ось в правой системе координат.
В цилиндрические координаты (р, θ, час) та же спираль параметризуется:
Круговая спираль радиуса а и наклон б/а (или шаг 2πb) описывается следующей параметризацией:
Другой способ математического построения спирали - построить комплексную функцию еxi как функция действительного числа Икс (увидеть Формула Эйлера).Значение Икс а действительная и мнимая части значения функции дают этому графику три реальных измерения.
Кроме вращения, переводы, и изменения масштаба, все правые спирали эквивалентны спирали, определенной выше. Эквивалентная левосторонняя спираль может быть построена несколькими способами, самый простой из которых - отрицать любой из Икс, у или z компоненты.
Длина дуги, кривизна и кручение
Длина круговой спирали радиуса а и наклон б/а (или шаг 2πb) выражается в прямоугольных координатах как
равно , его кривизна является и это кручение является Спираль имеет постоянную ненулевую кривизну и кручение.
Спираль - это вектор-функция
Таким образом, спираль может быть изменена в зависимости от , который должен быть единичной скоростью:
Единичный касательный вектор равен
Нормальный вектор
Его кривизна .
Единичный вектор нормали равен
Вектор бинормали равен
Его кручение .
Примеры
В Музыка, пространство поля часто моделируется спиралями или двойными спиралями, чаще всего выходящими из круга, например круг пятых, чтобы представить октавная эквивалентность.
Кристаллическая структура сложенная молекулярная спираль сообщает Лен и другие. в Helv. Чим. Acta., 2003, 86, 1598–1624.
Естественная левая спираль, созданная альпинист растение
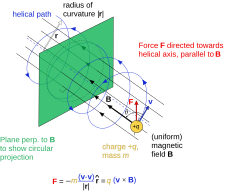
Заряженная частица в униформе магнитное поле следуя винтовой траектории
Смотрите также
Рекомендации
- ^ ἕλιξ В архиве 2012-10-16 в Wayback Machine, Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, на Персее
- ^ Вайсштейн, Эрик В. «Геликоид». MathWorld.
- ^ "Двойная спираль В архиве 2008-04-30 на Wayback Machine"Шандор Кабаи, Вольфрам Демонстрационный проект.
- ^ О'Нил, Б. Элементарная дифференциальная геометрия, 1961 стр.72
- ^ О'Нил, Б. Элементарная дифференциальная геометрия, 1961 стр.74
- ^ Изумия, С., Такеучи, Н. (2004) Новые специальные кривые и складывающиеся поверхности. Turk J Math В архиве 2016-03-04 в Wayback Machine, 28:153–163.
- ^ Меннингер, Т. (2013), Явная параметризация аппарата Френе наклонной спирали.. arXiv: 1302.3175 В архиве 2018-02-05 в Wayback Machine.
- ^ Вайсштейн, Эрик В. "Спираль". MathWorld.
<https://www.merriam-webster.com/dictionary/geometrical%20pitch











![t mapsto (a cos t, a sin t, bt), t in [0, T]](https://wikimedia.org/api/rest_v1/media/math/render/svg/93d3e0b26d648578d282662c605919e609ab3636)















![{ displaystyle mathbf {B} = mathbf {T} times mathbf {N} = { frac {1} { sqrt {a ^ {2} + b ^ {2}}}} { bigg [ } b sin { frac {s} { sqrt {a ^ {2} + b ^ {2}}}} mathbf {i} -b cos { frac {s} { sqrt {a ^ { 2} + b ^ {2}}}} mathbf {j} + a mathbf {k} { bigg]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a6f1f86f8adb11b23cae7fbcc4ba4a8e60dd456)
![{ displaystyle { frac {d mathbf {B}} {ds}} = { frac {1} {a ^ {2} + b ^ {2}}} { bigg [} b cos { frac {s} { sqrt {a ^ {2} + b ^ {2}}}} mathbf {i} + b sin { frac {s} { sqrt {a ^ {2} + b ^ {2 }}}} mathbf {j} +0 mathbf {k} { bigg]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e10826ada5a48b614c5f015e7b0cf436d8fdf9)