WikiDer > Эллиптический фильтр
| Линейный аналог электронные фильтры |
|---|
|
Простые фильтры |
An эллиптический фильтр (также известный как Фильтр Кауэра, названный в честь Вильгельм Кауэр, или как Золотарев фильтр, после Егор Золотарев) это фильтр обработки сигналов с уравновешенным рябь (Equiripple) поведение как в полоса пропускания и полоса задерживания. Количество пульсаций в каждой полосе регулируется независимо, и никакой другой фильтр такого же порядка не может иметь более быстрый переход в прирост между полоса пропускания и полоса задерживания, для данных значений пульсации (независимо от того, выровнена ли пульсация).[нужна цитата] В качестве альтернативы можно отказаться от возможности независимо настраивать пульсации полосы пропускания и полосы задерживания и вместо этого разработать фильтр, который максимально нечувствителен к изменениям компонентов.
Когда пульсация в полосе задерживания приближается к нулю, фильтр становится типом I. Фильтр Чебышева. Когда пульсация в полосе пропускания приближается к нулю, фильтр становится фильтром типа II. Фильтр Чебышева и, наконец, когда оба значения пульсации приближаются к нулю, фильтр становится Фильтр Баттерворта.
Прирост НЧ эллиптический фильтр как функция угловой частоты ω определяется как:
где Rп это пй порядок эллиптическая рациональная функция (иногда называемая рациональной функцией Чебышева) и
- это частота среза
- фактор пульсации
- коэффициент селективности
Значение коэффициента пульсации определяет пульсацию полосы пропускания, в то время как комбинация коэффициента пульсации и коэффициента селективности определяет пульсацию полосы задерживания.
Характеристики
- В полосе пропускания эллиптическая рациональная функция изменяется от нуля до единицы. Таким образом, коэффициент усиления полосы пропускания будет варьироваться от 1 до .
- В полосе задерживания эллиптическая рациональная функция изменяется от бесконечности до коэффициента дискриминации который определяется как:
- Таким образом, усиление полосы задерживания будет варьироваться от 0 до .
- В пределах эллиптическая рациональная функция становится Полином Чебышева, и поэтому фильтр становится Фильтр Чебышева I типа, с коэффициентом пульсации ε
- Поскольку фильтр Баттерворта является предельной формой фильтра Чебышева, отсюда следует, что в пределе , и такой, что фильтр становится Фильтр Баттерворта
- В пределах , и такой, что и , фильтр становится Фильтр Чебышева типа II с прибылью
Полюсы и нули

Нули усиления эллиптического фильтра будут совпадать с полюсами эллиптической рациональной функции, которые выводятся в статье о эллиптические рациональные функции.
Полюса усиления эллиптического фильтра могут быть получены способом, очень похожим на вывод полюсов усиления типа I. Фильтр Чебышева. Для простоты предположим, что частота среза равна единице. Полюса коэффициента усиления эллиптического фильтра будут нули знаменателя усиления. Использование комплексной частоты это означает, что:
Определение где cd () - Эллиптическая косинусная функция Якоби и используя определение эллиптических рациональных функций, получаем:
куда и . Решение для ш
где множественные значения обратной функции cd () указаны явно с использованием целочисленного индекса м.
Полюса эллиптической функции усиления тогда:
Как и в случае полиномов Чебышева, это может быть выражено в явно сложной форме (Lutovac & et al. 2001 г., § 12.8)
куда является функцией и и - нули эллиптической рациональной функции. выразим для всех п в терминах эллиптических функций Якоби или алгебраически для некоторых порядков, особенно для порядков 1,2 и 3. Для порядков 1 и 2 имеем
куда
Алгебраическое выражение для довольно вовлечен (см. Lutovac & et al. (2001 г., § 12.8.1)).
Вложенность эллиптические рациональные функции может использоваться для построения выражений более высокого порядка для :
куда .
Эллиптические фильтры с минимальной добротностью
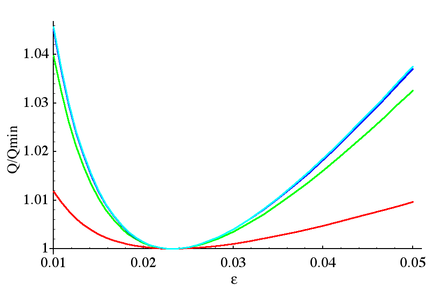
Видеть Lutovac & et al. (2001 г., § 12.11, 13.14).
Эллиптические фильтры обычно задаются, требуя определенного значения для пульсации полосы пропускания, пульсации полосы задерживания и резкости среза. Это обычно определяет минимальное значение порядка фильтрации, которое необходимо использовать. Еще одним соображением при проектировании является чувствительность функции усиления к значениям электронных компонентов, используемых для создания фильтра. Эта чувствительность обратно пропорциональна добротности (Добротность) полюсов передаточной функции фильтра. Добротность полюса определяется как:
и является мерой влияния полюса на функцию усиления. Для эллиптического фильтра случается, что для данного порядка существует взаимосвязь между коэффициентом пульсации и коэффициентом селективности, которая одновременно минимизирует добротность всех полюсов в передаточной функции:
В результате получается фильтр, который максимально нечувствителен к изменениям компонентов, но при этом теряется возможность независимо определять полосу пропускания и пульсации полосы задерживания. Для таких фильтров по мере увеличения порядка пульсация в обеих полосах будет уменьшаться, а скорость отсечки увеличиваться. Если кто-то решит использовать эллиптический фильтр с минимальной добротностью для достижения определенной минимальной пульсации в полосах фильтра вместе с определенной скоростью среза, необходимый порядок обычно будет больше, чем тот, который в противном случае потребовался бы без минимальной добротности. ограничение. Изображение абсолютного значения усиления будет очень похоже на изображение в предыдущем разделе, за исключением того, что полюса расположены по кругу, а не по эллипсу. Они не будут расположены равномерно и на оси ω будут нули, в отличие от Фильтр Баттерворта, полюса которого расположены в равномерно распределенном круге без нулей.
Сравнение с другими линейными фильтрами
Вот изображение, показывающее эллиптический фильтр рядом с другим распространенным типом фильтров, полученных с тем же количеством коэффициентов:
Как видно из изображения, эллиптические фильтры резче, чем все остальные, но они показывают рябь по всей полосе пропускания.
Смотрите также
- "EllipticFilterModel". Центр документации и языков Wolfram. Wolfram, Inc. Получено 2016-11-05. Расчет параметров эллиптического фильтра в системе Mathematica.
Рекомендации
- Дэниелс, Ричард В. (1974). Методы приближения для проектирования электронных фильтров. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-015308-6.
- Лутовац, Мирослав Д .; Тошич, Деян В .; Эванс, Брайан Л. (2001). Дизайн фильтров для обработки сигналов с использованием MATLAB и Mathematica. Нью-Джерси, США: Прентис Холл. ISBN 0-201-36130-2.










































