WikiDer > Пятимерное пространство - Википедия

2D ортогональная проекция из 5-куб

А пятимерное пространство это Космос с пятью размеры. Если интерпретировать физически, это на один больше, чем обычных трех пространственный измерения и четвертое измерение время используется в релятивистская физика.^[1] Это абстракция, которая часто встречается в математике, где она является законной конструкцией. В физика и математика, а последовательность из N числа можно понимать как представление место расположения в N-размерный Космос. Независимо от того, вселенная пятимерный - это предмет дискуссий.^{[нужна цитата]}

Физика

Большая часть ранних работ по пятимерному пространству была попыткой разработать теория, которая объединяет четверка фундаментальные взаимодействия в природе: сильный и слабый ядерные силы сила тяжести и электромагнетизм. Немецкий математик Теодор Калуца и Шведский физик Оскар Кляйн независимо разработал Теория Калуцы – Клейна в 1921 году, который использовал пятое измерение для объединения сила тяжести с электромагнитная сила. Хотя их подходы позже оказались по крайней мере частично неточными, эта концепция послужила основой для дальнейших исследований в прошлом веке.^[1]

Чтобы объяснить, почему это измерение нельзя наблюдать напрямую, Кляйн предположил, что пятое измерение будет свернуто в крошечную компактную петлю порядка 10^-33 сантиметры.^[1] Согласно его рассуждениям, он представлял свет как нарушение, вызванное рябью в высшем измерении, находящейся за пределами человеческого восприятия, подобно тому, как рыба в пруду может видеть только тени ряби на поверхности воды, вызванной каплями дождя.^[2] Хотя это и невозможно обнаружить, это косвенно подразумевает связь между, казалось бы, не связанными друг с другом силами. Теория Калуцы – Клейна пережила возрождение в 1970-х годах в связи с появлением теория суперструн и супергравитация: идея о том, что реальность состоит из колеблющихся нитей энергии, постулат, математически жизнеспособный только в десяти или более измерениях. Затем теория суперструн превратилась в более общий подход, известный как М-теория. М-теория предложила потенциально наблюдаемое дополнительное измерение в дополнение к десяти существенным измерениям, которые допускали бы существование суперструн. Остальные 10 измерений уплотнены, или «свернуты», до размера ниже субатомного уровня.^[1][2] Теория Калуцы – Клейна сегодня рассматривается как по существу калибровочная теория, с измерять будучи круговая группа.^{[нужна цитата]}

Пятое измерение трудно наблюдать напрямую, хотя Большой адронный коллайдер дает возможность зафиксировать косвенные доказательства его существования.^[1] Физики предполагают, что столкновения субатомных частиц, в свою очередь, порождают новые частицы в результате столкновения, в том числе гравитон что убегает из четвертого измерения, или брана, просачиваясь в пятимерную массу.^[3] М-теория могла бы объяснить слабость гравитации по отношению к другим фундаментальным силам природы, что можно увидеть, например, при использовании магнита для поднятия булавки со стола - магнит способен преодолевать гравитационное притяжение всего земля с легкостью.^[1]

Математические подходы были разработаны в начале 20 века, в которых пятое измерение рассматривалось как теоретическая конструкция. Эти теории ссылаются на Гильбертово пространство, концепция, которая постулирует бесконечное количество математических измерений, позволяющих неограниченное количество квантовых состояний. Эйнштейн, Бергманн и Bargmann позже попытался расширить четырехмерное пространство-время из общая теория относительности в дополнительное физическое измерение, чтобы включить электромагнетизм, хотя они и не увенчались успехом.^[1] В своей статье 1938 года Эйнштейн и Бергманн были одними из первых, кто представил современную точку зрения, согласно которой четырехмерная теория, совпадающая с Теория Эйнштейна-Максвелла на больших расстояниях выводится из пятимерной теории с полным симметрия во всех пяти измерениях. Они предположили, что электромагнетизм является результатом гравитационного поля, которое «поляризовано» в пятом измерении.^[4]

Главное новшество Эйнштейна и Бергманна состояло в том, чтобы всерьез рассматривать пятое измерение как физическую сущность, а не как оправдание для объединения метрический тензор и электромагнитный потенциал. Но затем они отказались, изменив теорию, нарушив ее пятимерную симметрию. Их рассуждения, предложенные Эдвард Виттен, заключалась в том, что более симметричная версия теории предсказывала существование нового дальнодействующего поля, которое одновременно безмассовый и скаляр, что потребовало бы фундаментальной модификации теории Эйнштейна. общая теория относительности.^[5] Пространство Минковского и Уравнения Максвелла в вакууме может быть встроен в пятимерный Тензор кривизны Римана.^{[нужна цитата]}

В 1993 г. физик Жерар т Хофт выдвинул голографический принцип, что объясняет, что информация о дополнительном измерении видна как кривизна в пространстве-времени с одним измерением меньше. Например, голограммы - это трехмерные изображения, размещенные на двухмерной поверхности, что придает изображению кривизну при движении наблюдателя. Точно так же в общей теории относительности четвертое измерение проявляется в наблюдаемых трех измерениях как траектория кривизны движущейся бесконечно малой (пробной) частицы. 'Т Хоофт предположил, что пятое измерение действительно ткань пространства-времени.^{[нужна цитата]}

Пятимерная геометрия

Согласно определению Кляйна, «геометрия - это изучение инвариантных свойств пространства-времени при преобразованиях внутри себя». Таким образом, геометрия пятого измерения изучает инвариантные свойства такого пространства-времени, когда мы движемся в нем, выраженные в формальных уравнениях.^[6]

Многогранники

В пяти или более измерениях только три правильные многогранники существовать. В пяти измерениях это:

1. В 5-симплекс из симплекс семейство, {3,3,3,3}, с 6 вершинами, 15 ребрами, 20 гранями (каждая равносторонний треугольник), 15 ячеек (каждая обычная тетраэдр) и 6 гиперэлементов (каждая по 5-элементный).
2. В 5-куб из гиперкуб семейство, {4,3,3,3}, с 32 вершинами, 80 ребрами, 80 гранями (каждая по квадрат), 40 ячеек (каждая по куб) и 10 гиперэлементов (каждая по тессеракт).
3. В 5-ортоплекс из кросс-многогранник семейство, {3,3,3,4}, с 10 вершинами, 40 ребрами, 80 гранями (каждая треугольник), 80 ячеек (каждая по тетраэдр) и 32 гиперячейки (каждая по a 5-элементный).

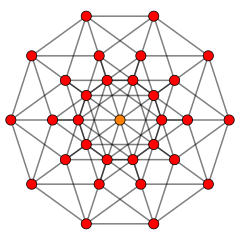
Важным однородным 5-многогранником является 5-полукруглый, h {4,3,3,3} имеет половину вершин 5-куба (16), ограниченных чередованием 5-элементный и 16 ячеек гиперячейки. В расширенный или же стерилизованный 5-симплексный - фигура вершины А₅ решетка, . Это и имеет двойную симметрию из его симметричной диаграммы Кокстера. Число поцелуев решетки, 30, представлено в ее вершинах.^[7] В выпрямленный 5-ортоплекс - фигура вершины D₅ решетка, . Его 40 вершин представляют собой номер поцелуя решетки и наивысший для размерности 5.^[8]

Правильные и полуправильные многогранники в пяти измерениях
(Отображается в виде ортогональных проекций в каждом Самолет Кокстера симметрии)

А5	Aut (A5)	B5			D5
5-симплекс {3,3,3,3}	Стерилизованный 5-симплексный	5-куб {4,3,3,3}	5-ортоплекс {3,3,3,4}	Ректифицированный 5-ортоплекс г {3,3,3,4}	5-полукруглый ч {4,3,3,3}

Гиперсфера

А гиперсфера в 5-м пространстве (также называемом 4-сфера из-за 4-мерной поверхности) состоит из множества всех точек в 5-м пространстве на фиксированном расстоянии р из центральной точки P. Гиперобъем, заключенный в эту гиперповерхность, равен:

${ displaystyle V = { frac {8 pi ^ {2} r ^ {5}} {15}}}$

Смотрите также

• 5-коллекторный
• Сила тяжести
• Гиперсфера
• Список правильных 5-многогранников

Рекомендации

дальнейшее чтение

• Вессон, Пол С. (1999). Пространство-время-материя, современная теория Калуцы-Клейна. Сингапур: World Scientific. ISBN 981-02-3588-7.
• Вессон, Пол С. (2006). Пятимерная физика: классические и квантовые последствия космологии Калуцы-Клейна. Сингапур: World Scientific. ISBN 981-256-661-9.
• Вейль, Германн, Raum, Zeit, Materie, 1918. 5 изд. к изд. 1922 г. с примечаниями Юргена Элерса, 1980. пер. 4-е изд. Генри Брозе, 1922 год Пространственно-временная материя, Метуэн, представ. 1952 г. Дувр. ISBN 0-486-60267-2.

внешняя ссылка

• Анаглиф пятимерного гиперкуба в гипер-перспективе