WikiDer > Восьмимерное пространство

Eight-dimensional space

В математика, последовательность п действительные числа можно понимать как место расположения в п-размерный Космос. Когда п = 8, множество всех таких локаций называется 8-мерное пространство. Часто такие пространства изучаются как векторные пространства, без понятия расстояния. Восьмимерный Евклидово пространство восьмимерное пространство, снабженное Евклидова метрика.

В более общем смысле термин может относиться к восьмимерному векторному пространству над любым поле, например, восьмимерный сложный векторное пространство, имеющее 16 реальных измерений. Это также может относиться к восьмимерному многообразие например, 8-сфера, или множество других геометрических конструкций.

Геометрия

8-многогранник

А многогранник в восьми измерениях называется 8-многогранником. Наиболее изученными являются правильные многогранники, из которых только три в восьми измерениях: the 8-симплекс, 8-куб, и 8-ортоплекс. Более широкая семья - это равномерные 8-многогранники, построенные из областей фундаментальной симметрии отражения, каждая область определяется Группа Коксетера. Каждый равномерный многогранник определяется окольцованным Диаграмма Кокстера-Дынкина. В 8-полукруглый - единственный многогранник из D₈ семья и 4₂₁, 2₄₁, и 1₄₂ многогранники из E₈ семья.

Правильные и однородные многогранники в восьми измерениях
(Отображается в виде ортогональных проекций в каждом Самолет Кокстера симметрии)
А₈	B₈				D₈
8-симплекс {3,3,3,3,3,3,3}	8-куб {4,3,3,3,3,3,3}		8-ортоплекс {3,3,3,3,3,3,4}		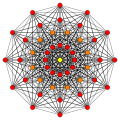8-полукруглый ч {4,3,3,3,3,3,3}
E₈
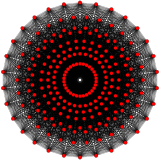4₂₁ {3,3,3,3,3^2,1}		2₄₁ {3,3,3^4,1}		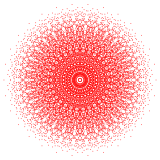1₄₂ {3,3^4,2}

7-сфера

В 7-сфера или гиперсфера в восьми измерениях - это семимерная поверхность, равноудаленная от точки, например Происхождение. Имеет символ $S 7$ , с формальным определением 7-сферы радиуса р из

{ Displaystyle S ^ {7} = left {x in mathbb {R} ^ {8}: | x | = r right }.}

Объем пространства, ограниченного этой 7-сферой, равен

{ displaystyle V_ {8} , = { frac { pi ^ {4}} {24}} , R ^ {8}}

что составляет 4.05871 × р⁸, или 0,01585 от 8-куб который содержит 7-сферу.

Проблема с поцелуями

В проблема с числом поцелуев была решена в восьми измерениях благодаря существованию 4₂₁ многогранник и связанный с ним решетка. Число поцелуев в восьми измерениях 240.

Октонионы

Октонионы - это нормированная алгебра с делением над действительными числами, самой большой такой алгеброй. Математически они могут быть заданы 8-ми кортежами действительных чисел, поэтому формируют 8-мерное векторное пространство над вещественными числами, причем добавление векторов является сложением в алгебре. Нормированная алгебра - это алгебра, произведение которой удовлетворяет

{ Displaystyle | ху | Leq | х | | у |}

для всех Икс и у в алгебре. Нормированный алгебра с делением дополнительно должен быть конечномерным и обладать тем свойством, что каждый ненулевой вектор имеет уникальный мультипликативный обратный. Теорема Гурвица запрещает такой конструкции существовать в размерах, отличных от 1, 2, 4 или 8.

Бикватернионы

Усложненный кватернионы ${ Displaystyle mathbb {C} otimes mathbb {H}}$ , или же "бикватернионы, "- восьмимерная алгебра, относящаяся к Уильям Роуэн Гамильтонработы в 1850-е гг. Эта алгебра эквивалентна (т. Е. изоморфный) к Алгебра Клиффорда ${ Displaystyle C ell _ {2} ( mathbb {C})}$ и Алгебра Паули. Он также был предложен в качестве практического или педагогического инструмента для выполнения расчетов в специальная теория относительности, и в этом контексте называется Алгебра физического пространства (не путать с Алгебра пространства-времени, который является 16-мерным.)

v т е Измерение
Размерные пространства	Векторное пространство Евклидово пространство Аффинное пространство Проективное пространство Бесплатный модуль Многообразие Алгебраическое многообразие Пространство-время
Другие размеры	Krull Покрытие Лебега Индуктивный Хаусдорф Минковский Фрактал Степени свободы
Многогранники и формы	Гиперплоскость Гиперповерхность Гиперкуб Гиперсфера Гиперпрямоугольник Демигиперкуб Кросс-многогранник Симплекс
Размеры по номеру	Нуль Один Два Три Четыре Пять Шесть Семь 8 9 п-размеры Отрицательные размеры
Категория

Navigation