WikiDer > Гномоническая проекция

Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. (Февраль 2019 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Гномоническая проекция части северного полушария с центром на географическом Северном полюсе

Гномоническая проекция с Индикатриса Тиссо деформации

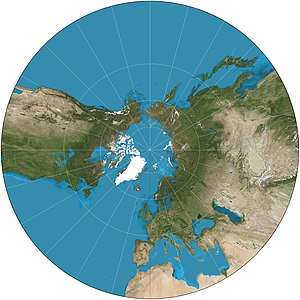
А гномоническая картографическая проекция отображает все большие круги в виде прямых линий, в результате чего любой отрезок прямой линии на гномонической карте показывает геодезический, кратчайший маршрут между двумя конечными точками сегмента. Это достигается путем отбрасывания точек поверхности сферы на касательная плоскости, при каждой посадке, когда луч из центра сферы проходит через точку на поверхности и затем попадает в плоскость. В точке касания искажения не происходит, но искажение быстро увеличивается по мере удаления от нее. Менее половины сфера можно спроецировать на конечную карту.^[1] Следовательно, прямолинейный фотообъектив, основанный на гномоническом принципе, не может отображать более 180 градусов.

История

Гномонический проекция считается старейшей картографической проекцией, разработанной Фалес в 6 веке до нашей эры^[1]:164. Путь тени или светового пятна в солнечные часы на основе узлов прослеживает то же самое гиперболы образованный параллелями на гномонической карте.

Характеристики

Гномоническая проекция идет от центра сферы к плоскости, касательной к сфере (рис. 1 ниже). Сфера и плоскость соприкасаются в точке касания. Большие круги превращаются в прямые через гномоническую проекцию. С меридианы (линии долготы) и экватор большие круги, они всегда показаны прямыми линиями на гномонической карте. Поскольку проекция идёт из центра сферы, гномоническая карта может представлять менее половины площади сферы. Искажение масштаба карты увеличивается от центра (точки касания) к периферии.^[1]

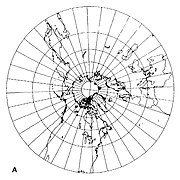
• Если точка касания является одной из полюса тогда меридианы будут радиальными и равномерно разнесенными (рис. 2 ниже). Экватор нельзя показать так, как он находится на бесконечность во всех направлениях. Другой параллели (линии широты) изображаются концентрическими круги.

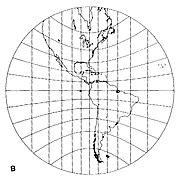
• Если точка касания находится на экваторе, то меридианы параллельны, но не равномерно разнесены (рис. 3 ниже). Экватор - это прямая линия, перпендикулярная меридианам. Другие параллели изображены как гиперболы.

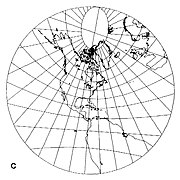
• Если точка касания не находится на полюсе или экваторе, тогда меридианы являются радиально направленными наружу прямыми линиями от полюса, но не на равных расстояниях (рис. 4 ниже). Экватор - это прямая линия, перпендикулярная только одному меридиану, что указывает на то, что проекция не является прямой. конформный. Другие параллели изображены как конические секции.

Как и все азимутальный проекции, углы от точки касания сохраняются. Расстояние на карте от этой точки является функцией р(d) истинного расстояния d, данный

${ Displaystyle г (д) = р , загар { гидроразрыва {d} {R}}}$

куда р это радиус Земли. Радиальный масштаб

${ displaystyle r '(d) = { frac {1} { cos ^ {2} { frac {d} {R}}}}}$

и поперечный шкала

${ displaystyle { frac {1} { cos { frac {d} {R}}}}}$

поэтому поперечный масштаб увеличивается наружу, а радиальный - еще больше.

Использовать

Гномонические проекции используются в сейсмический работают, потому что сейсмические волны имеют тенденцию перемещаться по большим кругам. Они также используются флот в заговоре пеленгование подшипники, поскольку радио сигналы движутся по большим кругам. Метеоры также путешествуют по большим кругам, с Гномоническим Атлас Брно 2000.0 будучи ИМОРекомендуемый набор звездных карт для визуальных наблюдений за метеорами. Пилоты самолетов и кораблей используют проекцию, чтобы найти кратчайший маршрут от пункта старта до пункта назначения.

Гномоническая проекция широко используется в фотография, где это называется прямолинейный проекция. Поскольку они эквивалентны, то же средство просмотра, которое используется для фотографических панорам, может использоваться для визуализации гномонических карт. (просмотр как интерактивная панорама на 360 °).

Гномоническая проекция используется в астрономии, когда точка касания центрируется на интересующем объекте. В данном случае проецируемая сфера - это небесная сфера, р = 1, а не поверхность Земли.

Сравнение Гномоническая проекция и некоторые азимутальные проекции с центром на 90 ° с.ш. в том же масштабе, упорядоченные по высоте проекции в радиусах Земли. (нажмите для подробностей)

Смотрите также

• Список картографических проекций
• Модель Бельтрами – Клейнааналогичное отображение гиперболическая плоскость

Рекомендации

• Calabretta, Mark R .; Грейзен, Эрик В. (19 июля 2002 г.). "Представления небесных координат в FITS (Документ II)". Астрономия и астрофизика. 395: 1077–1122. arXiv:Astro-ph / 0207413. Дои:10.1051/0004-6361:20021327.

внешняя ссылка

Викискладе есть медиафайлы по теме Гномоническая проекция.

• Гномоническая проекция