WikiDer > Навигация по большому кругу
Навигация по большому кругу или же ортодромная навигация (относится к ортодромический курс; от Греческий ορθóς, прямой угол, и δρóμος, путь) - это практика навигация судно (a корабль или же самолет) вдоль большой круг. Такие маршруты дают кратчайшие расстояние между двумя точками земного шара.[1]
Курс
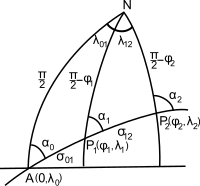
Путь большого круга можно найти, используя сферическая тригонометрия; это сферическая версия обратная геодезическая задача.Если навигатор начинается в п1 = (φ1, λ1) и планирует путешествие по большому кругу в точку в точку п2 = (φ2, λ2) (см. рис.1, φ - широта, положительное значение на север, а λ - долгота, положительное значение на восток), начальный и конечный курсы α1 и α2 даны формулы решения сферического треугольника
где λ12 = λ2 - λ1[примечание 1]и квадранты α1, α2 определяются знаками числителя и знаменателя в касательных формулах (например, с помощью atan2 функция). центральный угол между двумя точками σ12, дан кем-то
(Числитель этой формулы содержит величины, которые использовались для определения α1.) Тогда расстояние по большому кругу будет s12 = рσ12, куда р - предполагаемый радиус Земли, а σ12 выражается в радианы.С использованием средний радиус Земли, р = р1 ≈ 6,371 км (3959 миль) дает результаты для расстояния s12 которые находятся в пределах 1% отгеодезическое расстояние для WGS84 эллипсоид.
Поиск путевых точек
Чтобы найти путевые точки, то есть положения выбранных точек на большом круге междуп1 и п2, мы сначала экстраполируем большой круг обратно на его узел А, точка, в которой большой круг пересекает экватор в северном направлении: пусть долгота этой точки будет λ0 - см. Рис. 1. Азимут в этой точке α0, дан кем-то
Пусть угловые расстояния по большому кругу от А к п1 и п2 быть σ01 и σ02 соответственно. Затем используя Правила Напьера у нас есть
- (Если φ1 = 0 и α1 = 1⁄2π, используйте σ01 = 0).
Это дает σ01, откуда σ02 = σ01 + σ12.
Долгота в узле находится из
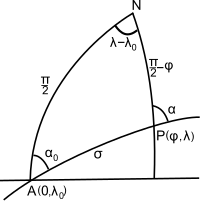
Наконец, вычислите положение и азимут в произвольной точке, п (см. рис. 2), сферическим вариантом прямая геодезическая задача.[примечание 5] Правила Непьера дают
В atan2 функция должна использоваться для определения σ01, λ и α. Например, чтобы найти середину пути, подставьте σ =1⁄2(σ01 + σ02); или найти точку на расстоянии d из начальной точки возьмем σ = σ01 + d/р. Точно так же вершина, точка наибольшей широты на большой окружности, находится заменой σ = +1⁄2π. Для параметризации маршрута по долготе может быть удобно использовать
Широты через равные интервалы долготы могут быть найдены, а полученные положения перенесены на карту Меркатора, что позволяет аппроксимировать большой круг серией румба. Определенный таким образом путь дает большой эллипс соединение конечных точек при условии координат интерпретируются как географические координаты на эллипсоиде.
Эти формулы применимы к сферической модели Земли. Они также используются при решении большого круга на вспомогательная сфера который является устройством для поиска кратчайшего пути, или геодезический, онан эллипсоид вращения; посмотреть статью о геодезические на эллипсоиде.
Пример
Вычислить маршрут большого круга от Вальпараисо, φ1 = −33 °, λ1 = −71,6 °, доШанхай, φ2 = 31,4 °, λ2 = 121.8°.
Формулы для курса и расстояния дают λ12 = −166.6°,[примечание 8]α1 = −94,41 °, α2 = −78,42 °, а σ12 = 168,56 °. Принимая радиус земли бытьр = 6371 км, расстояниеs12 = 18743 км.
Чтобы вычислить точки на маршруте, сначала найдите α0 = −56,74 °, σ1 = −96,76 °, σ2 = 71,8 °, λ01 = 98,07 ° и λ0 = −169,67 °. Затем для вычисления средней точки маршрута (например) возьмите σ =1⁄2(σ1 + σ2) = −12,48 °, и решаем для φ = −6,81 °, λ = −159,18 ° и α = −57,36 °.
Если геодезическая рассчитана точно на WGS84 эллипсоид,[4] результат α1 = −94,82 °, α2 = −78.29 °, иs12 = 18752 км. Середина геодезической: φ = −7,07 °, λ = −159,31 °, α = −57,45 °.
Гномоническая карта
Прямая линия, проведенная на гномоническая карта был бы отличный круговой трек. Когда это передается в График Меркатора, он становится кривой. Позиции переносятся с удобным интервалом долгота и это нанесено на карту Меркатора.
Смотрите также
- Картушка
- Большой круг
- Расстояние большого круга
- Большой эллипс
- Геодезические на эллипсоиде
- Географическое расстояние
- Изоазимутал
- Локсодромная навигация
- карта
- Морские песочные часы
- Линия румба
- Сферическая тригонометрия
- Сеть Роза ветров
Примечания
- ^ В статье о расстояния по дуге, обозначение Δλ = λ12и Δσ = σ12 используется. Обозначения в этой статье необходимы для устранения различий между другими точками, например, λ01.
- ^ Более простая формула
- ^ Эти уравнения для α1, α2, σ12 подходят для реализации на современных калькуляторах и компьютерах. Для ручных вычислений с логарифмами,Деламбреаналогии[2] обычно использовались:
- ^ Более простая формула
- ^ Прямая геодезическая задача, определение положения п2 данный п1, α1,и s12, также можно решить с помощьюформулы решения сферического треугольника, следующее,
- ^ Более простая формула
- ^ Используются следующие:
- ^ λ12уменьшается до диапазона [-180 °, 180 °] путем добавления или вычитания 360 ° по мере необходимости
Рекомендации
- ^ Адам Вайнтрит; Томаш Нойман (7 июня 2011 г.). Методы и алгоритмы навигации: морская навигация и безопасность морских перевозок.. CRC Press. С. 139–. ISBN 978-0-415-69114-7.
- ^ Тодхантер, И. (1871). Сферическая тригонометрия (3-е изд.). Макмиллан. п.26.
- ^ Маккоу, Г. Т. (1932). «Длинные линии на Земле». Обзор обзора империи. 1 (6): 259–263. Дои:10.1179 / sre.1932.1.6.259.
- ^ Карни, К. Ф. Ф. (2013). «Алгоритмы геодезических». J. Геодезия. 87 (1): 43–55. Дои:10.1007 / s00190-012-0578-z.
внешняя ссылка
- Большой круг - из MathWorld Описание Великого Круга, рисунки и уравнения. Mathworld, Wolfram Research, Inc. c1999 г.
- Картограф Великого Круга Интерактивный инструмент для построения маршрутов по большому кругу.
- Калькулятор Большого Круга начальный курс и расстояние между двумя точками.
- Расстояние по большому кругу Графический инструмент для рисования больших кругов на картах. Также показывает расстояние и азимут в таблице.
- Программа помощи Google для ортодромной навигации