WikiDer > Большой сложный икосододекаэдр
| Большой сложный икосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 32, E = 60 (30x2) V = 12 (χ = -16) |
| Лица по сторонам | 20{3}+12{5/2} |
| Символ Wythoff | 5 | 3 5/3 |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | U-, C-, W- |
| Двойной многогранник | Большой сложный икосидодекакрон |
| Фигура вершины | 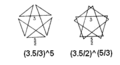 (3.5/3)5 (3.5/2)5/3 |
| Акроним Bowers | Gacid |
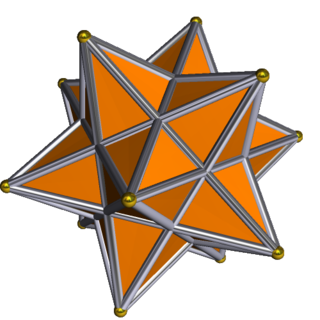
В геометрия, то большой сложный икосододекаэдр вырожденный однородный звездный многогранник. У него 12 вершин, 60 (сдвоенных) ребер и 32 грани, 12 пентаграммы и 20 треугольники. Все ребра удваиваются (что делает его вырожденным), разделяют 4 грани, но рассматриваются как два перекрывающихся ребра как топологический многогранник.
Может быть построен из ряда различных фигуры вершин.
Как соединение
Большой сложный икосододекаэдр можно считать сложный из малый звездчатый додекаэдр, {5 / 2,5} и большой икосаэдр, {3,5 / 2}, имеющие одни и те же вершины и ребра, в то время как второе скрыто и полностью содержится внутри первого.
Его двумерный аналог был бы составной частью обычного пятиугольник, {5} и обычный пентаграмма, {5/2}. Эти формы будут иметь общие вершины, аналогично тому, как их трехмерный эквивалент имеет общие ребра.
|
Смотрите также
- Малый сложный икосододекаэдр
- Малый сложный ромбикосододекаэдр
- Сложный ромбидодекадодекаэдр
- Большой сложный ромбикосододекаэдр
Рекомендации
- Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954), "Равномерные многогранники", Философские труды Лондонского королевского общества. Серия А. Математические и физические науки., 246 (916): 401–450, Дои:10.1098 / рста.1954.0003, ISSN 0080-4614, JSTOR 91532, МИСТЕР 0062446, S2CID 202575183 (Таблица 6, вырожденные случаи)
- Вайсштейн, Эрик В. «Большой сложный икосододекаэдр». MathWorld.
- Клитцинг, Ричард. "Трехмерные однородные многогранники o5 / 3x3o5 * a и o3 / 2x5 / 2o5 * a - gacid".





