WikiDer > Джеймс Грегори (математик)

James Gregory (mathematician)
Джеймс Грегори
Джеймс Грегори.jpeg
Джеймс Грегори (1638–1675)
РодившийсяНоябрь 1638
Drumoak, Абердиншир, Шотландия
УмерОктябрь 1675 г. (36 лет)
Эдинбург, Шотландия
НациональностьШотландский
ГражданствоШотландия
Альма-матерМаришаль Колледж, Университет Абердина
Университет Падуи
ИзвестенГригорианский телескоп
Дифракционная решетка
Основная теорема исчисления
Коэффициенты Грегори
Научная карьера
ПоляМатематика
Астрономия
УчрежденияСент-Эндрюсский университет
Эдинбургский университет
ВлиянияСтефано дельи Анджели
Под влияниемДэвид Грегори
Примечания

Джеймс Грегори ФРС (Ноябрь 1638 - октябрь 1675) был шотландским математиком и астроном. Его фамилия иногда пишется как Грегори, оригинальное шотландское написание. Он описал ранний практический дизайн для отражающий телескоп - в Григорианский телескоп - и добился успехов в тригонометрия, открывая бесконечная серия представления для нескольких тригонометрических функций.

В его книге Geometriae Pars Universalis (1668)[1] Грегори привел как первое опубликованное заявление, так и доказательство основная теорема исчисления (сформулировано с геометрической точки зрения и только для особого класса кривых, рассмотренных в более поздних версиях теоремы), за что он был признан Исаак Барроу.[2][3][4][5][6][7][8]

биография

Младший из трех детей Джона Грегори, Епископальный Церковь Шотландии министр, Джеймс родился в особняк в Drumoak, Абердиншир, и первоначально получил домашнее образование у своей матери, Джанет Андерсон (~ 1600–1668). Именно его мать наделила Грегори аппетитом к геометрия, ее дядя - Александр Андерсон (1582–1619) - был учеником и редактором французского математика Viète. После смерти отца в 1651 году его старший брат Давид взял на себя ответственность за его образование. Он присутствовал Абердинская гимназия, а потом Маришаль Колледж с 1653–1657, окончил AM в 1657 году.

В 1663 году он отправился в Лондон, встретив Джон Коллинз и товарищ шотландец Роберт Морей, один из основателей Королевское общество. В 1664 г. он отправился в Университет Падуи, в Венецианская Республика, проходя через Фландрия, Париж и Рим в пути. В Падуе он жил в доме своего земляка. Джеймс Кэдденхед, профессор философии, и его преподавал Стефано Анджели.

По возвращении в Лондон в 1668 году он был избран Член Королевского общества, перед поездкой в Сент-Эндрюс в конце 1668 г. занял свой пост первым Regius профессор математики, должность, созданная для него Карл II, вероятно, по просьбе Роберта Морея.

Он был последовательно профессором в Сент-Эндрюсский университет и Эдинбургский университет.

Он женился на Мэри, дочери Джордж Джеймсон, художник и вдова Джона Бернета из Элрика, Абердин; их сын Джеймс был профессором физики в Королевский колледж, Абердин. Он был дедушкой Джон Грегори (FRS 1756); дядя Дэвид Грегори (FRS 1692) и брат Дэвид Грегори (1627–1720), врач и изобретатель.

Примерно через год после вступления в кафедру математики в ЭдинбургДжеймс Грегори перенес инсульт, рассматривая спутники Юпитера со своими учениками. Он умер несколько дней спустя в возрасте 36 лет.

Опубликованные работы

Vera circi et hyperbolae quadratura, 1667

Optica Promota

в Optica Promota, опубликованный в 1663 году, Грегори описал свой дизайн для отражающий телескоп, "Григорианский телескоп". Он также описал метод использования транзит Венеры для измерения расстояния Земли от Солнца, за что позже выступил Эдмунд Галлей и принят в качестве основы для первого эффективного измерения Астрономический блок.

Vera Circuli et Hyperbolae Quadratura

Перед отъездом из Падуи Грегори опубликовал Vera Circuli et Hyperbolae Quadratura (1667 г.), в котором он аппроксимировал площади круг и гипербола со сходящимся рядом:

[Джеймсу Грегори] нельзя отрицать авторство многих любопытных теорем о связи круга с вписанный и ограниченные многоугольники, и их отношение друг к другу. Посредством этих теорем он дает с бесконечно меньшими трудностями, чем при обычных вычислениях,… меру окружности и гиперболы (и, следовательно, построение логарифмы) до более чем двадцати десятичных знаков. По примеру Гюйгенс, он также дал построения прямых, равных дуги круга, а погрешность еще меньше.[9]

"Первое доказательство основная теорема исчисления и открытие Серия Тейлор оба могут быть отнесены к нему ".[10][11]

В книге также есть дополнения к серии грех(Икс), потому что(Икс), arcsin (Икс) и arccos (Икс). Грегори, вероятно, не знал, что самые ранние изложения этих расширений были сделаны Мадхава в Индии в 14 веке. Книга была переиздана в 1668 году с приложением: Geometriae Pars, в котором Грегори объяснил, как объемы твердые тела вращения можно определить.

Григорианский телескоп

Схема григорианского телескопа-рефлектора.
Основная статья: Григорианский телескоп

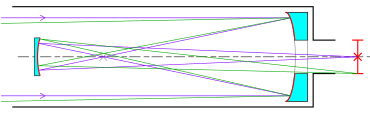
В его 1663 г. Optica PromotaДжеймс Грегори описал свой отражающий телескоп который стал известен под его именем - григорианский телескоп. Грегори указал, что телескоп-рефлектор с параболическое зеркало исправит сферическая аберрация так же хорошо как Хроматическая аберрация видел в преломляющие телескопы. В своей конструкции он также поместил вогнутую вторичное зеркало с эллиптической поверхностью за фокальной точкой параболического главное зеркало, отражая изображение обратно через отверстие в главном зеркале, где его можно было бы удобно рассматривать. По его собственному признанию, Грегори не обладал практическими навыками, и он не мог найти оптика, способного его построить.[12]

Конструкция телескопа привлекла внимание нескольких человек в научном учреждении, таких как Роберт Гук, оксфордский физик, который в итоге построил телескоп 10 лет спустя, и сэр Роберт Морей, эрудит и член-основатель Королевское общество.

Телескопы григорианской конструкции сегодня используются редко, так как другие типы телескопов-отражателей, как известно, более эффективны для стандартных приложений. Григорианская оптика также используется в радиотелескопы Такие как Аресибо, на котором изображен «григорианский купол».[13]

Математика

Следующий отрывок взят из Пантология. Новая (кабинетная) циклопедия (1813)

Мистер Джеймс Грегори был человеком очень проницательного и проницательного гения. ... Самая яркая часть его характера была в его математическом гении как изобретателе, который был первоклассным; как явствует из ... его изобретений и открытий, [которые включают] квадратуру круга и гиперболы, посредством бесконечного сходящегося ряда; его метод преобразования кривых; геометрическая демонстрация Лорда Браункера ряд для возведения в квадрат гиперболы - его демонстрация того, что линия меридиана аналогична шкале логарифмических тангенсов половинных дополнений широты; он также изобрел и геометрически продемонстрировал с помощью гиперболы очень простой сходящийся ряд для логарифмов; он отправил в Г-н Коллинз решение известного Кеплеровская проблема бесконечной серией; он открыл метод рисования Касательные строить кривые геометрически, без предварительных расчетов; правило прямого и обратного метода касательных, основанное на одном принципе ( истощения) с тем из флюксии, и не сильно отличается от него способом нанесения; ряд по длине дуги окружности от касательной и наоборот; а также для секущей, логарифмической касательной и секущей, и наоборот. Они, а также другие, для измерения длины эллиптических и гиперболических кривых, были отправлены мистеру Коллинзу в обмен на полученные от него Ньютона, в котором он последовал элегантному примеру этого автора, изложив свою серию простыми словами, независимыми друг от друга.[14]

Другая работа

В 1671 году, а может быть и раньше, он установил теорему о том, что

,

результат верен только в том случае, если θ лежит между - (1/4) π и (1/4) π. Эта формула позже использовалась для вычисления цифр π, хотя позже были обнаружены более эффективные формулы.

Джеймс Грегори открыл дифракционная решетка мимо Солнечный свет через птицу пух Перо и наблюдение полученной дифракционной картины.[15] В частности, он наблюдал расщепление солнечного света на составляющие его цвета - это произошло через год после того, как Ньютон сделал то же самое с призма и это явление все еще оставалось весьма спорным.

Круглое колесо не подходит для неровных поверхностей, и Грегори разработал подходящее «адаптируемое колесо», используя Преобразование Григория.[16]

Грегори, восторженный сторонник Ньютона, позже поддерживал с ним дружескую переписку и включил его идеи в собственное учение, идеи, которые в то время были противоречивыми и считались довольно революционными.

Кратер Грегори на Луне назван в его честь. Он был дядей математика Дэвид Грегори.

Работает

Смотрите также

Рекомендации

  1. ^ Грегори, Джеймс (1668). Geometriae Pars Universalis. Museo Galileo: Patavii: typis heredum Паули Фрамботти.
  2. ^ Заместитель декана колледжа Уильям Джонстон и профессор Колледжа математического центра Стодхилла; Алекс Макаллистер, доцент колледжа математического центра (26 июня 2009 г.). Переход к высшей математике: обзорный курс: обзорный курс. Oxford University Press. стр. 329–. ISBN 978-0-19-971866-5.
  3. ^ Эдмунд Ф. Робертсон. Джеймс Грегори: региональный профессор математики.
  4. ^ Майкл Науэнберг. Барроу и Лейбниц об основной теореме исчисления.
  5. ^ Эндрю Лихи. Евклидов подход к FTC - доказательство FTC Грегори.
  6. ^ Итан Д. Блох. Реальные числа и реальный анализ, стр. 316.
  7. ^ Роджер Л. Кук (14 февраля 2011 г.). История математики: краткий курс. Джон Уайли и сыновья. С. 467–. ISBN 978-1-118-03024-0.
  8. ^ Д. Дж. Струик. Справочник по математике, 1200-1800 гг.. Издательство Гарвардского университета. С. 262–. ISBN 978-0-674-82355-6.
  9. ^ Жан Монтукла (1873) История квадратуры круга, Переводчик Дж. Бабина, редактор Уильяма Александра Майерса, стр. 23, ссылка с HathiTrust
  10. ^ У. В. Роуз Болл (1908) Краткая история математики, Четвертый выпуск
  11. ^ Транскрипция Д. Р. Уилкинса
  12. ^ Биографический словарь выдающихся шотландцев Роберта Чемберса, Томаса - стр. 175
  13. ^ "Большое блюдо Джима Кордеса". Получено 22 ноября 2007.
  14. ^ Джон Мейсон Гуд, Олинтус Гилберт Грегори, Ньютон Босворт, Pantologia A new (кабинет) cyclopædi (1813)
  15. ^ Письмо Джеймса Грегори Джону Коллинзу от 13 мая 1673 г. Перепечатано на: Переписка ученых семнадцатого века ...., изд. Стивен Джордан Риго (Оксфорд, Англия: Oxford University Press, 1841), т. 2, страницы 251–255; особенно см. стр. 254. Доступно в Интернете по адресу: Books.Google.com.
  16. ^ Мазурель, Кристоф. «Обобщение колеса или адаптируемого колеса (введение в преобразование Грегори)» (PDF) - через http://christophe.masurel.free.fr/.

дальнейшее чтение

внешняя ссылка