WikiDer > Параболический отражатель

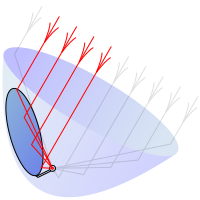
А параболический (или же параболоид или параболоидный) отражатель (или же блюдо или зеркало) это отражающий поверхность, используемая для сбора или проецирования энергия такие как свет, звук, или же радиоволны. Его форма является частью круговой параболоид, то есть поверхность, порожденная парабола вращается вокруг своей оси. Параболический отражатель преобразует входящий плоская волна продвигаясь вдоль оси в сферическая волна сходятся к фокусу. И наоборот, сферическая волна, порожденная точечный источник помещен в фокус отражается в плоскую волну, распространяющуюся как коллимированный пучок по оси.
Параболические отражатели используются для сбора энергии от удаленного источника (например, звуковых волн или входящих звезда свет). Поскольку принципы отражение обратимы, параболические отражатели могут также использоваться для коллимации излучения изотропного источника в параллельный луч.[1] В оптика, параболические зеркала используются для сбора света в отражающие телескопы и солнечные печи, и направить луч света в фонарики, прожекторы, сценические прожекторы, и автомобильные фары. В радио параболические антенны используются для излучения узкого луча радиоволны за точка-точка коммуникации в Спутниковые тарелки и микроволновое реле станций, а также для определения местоположения самолетов, кораблей и транспортных средств в радар наборы. В акустика, параболические микрофоны используются для записи далеких звуков, таких как крики птиц, в спортивных репортажах и для подслушивания частных разговоров в шпионаж и правоохранительные органы.
Теория
Эта секция не цитировать любой источники. (Ноябрь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Строго говоря, трехмерная форма отражателя называется параболоид. Парабола - это двухмерная фигура. (Различия такие же, как между сферой и кругом.) Однако на неформальном языке слово парабола и связанное с ним прилагательное параболический часто используются вместо параболоид и параболоидный.
Если парабола расположена в декартовых координатах с ее вершиной в начале координат и осью симметрии вдоль оси y, так что парабола открывается вверх, ее уравнение выглядит следующим образом: , где его фокусное расстояние. (Видеть "Парабола # В декартовой системе координат".) Соответственно, размеры симметричной параболоидальной тарелки связаны уравнением: где фокусное расстояние, - глубина тарелки (измеряется по оси симметрии от вершины до плоскости обода), а - радиус блюда от центра. Все единицы измерения радиуса, точки фокусировки и глубины должны быть одинаковыми. Если известны две из этих трех величин, это уравнение можно использовать для расчета третьей.
Для определения диаметра тарелки нужен более сложный расчет. измеряется по его поверхности. Иногда его называют «линейным диаметром», и он равен диаметру плоского круглого листа материала, обычно металла, который имеет правильный размер, который нужно разрезать и согнуть для изготовления блюда. При расчетах полезны два промежуточных результата: (или эквивалент: и где и определены, как указано выше. Диаметр тарелки, измеренный по поверхности, затем определяется как: где означает натуральный логарифм из , т.е. его логарифм по основанию "е".
Объем блюда определяется как где символы определены, как указано выше. Это можно сравнить с формулами для объемов цилиндр а полушарие где и конус - это площадь апертуры тарелки, площадь, ограниченная ободком, пропорциональная количеству солнечного света, которое рефлекторная тарелка может перехватить. Площадь вогнутой поверхности блюда можно найти, используя формулу площади для поверхность вращения который дает . предоставление . Доля света, отраженного тарелкой от источника света в фокусе, определяется выражением , где и определены, как указано выше.
Параболический отражатель функционирует благодаря геометрическим свойствам параболоидальной формы: любой входящий луч которая параллельна оси тарелки, будет отражена в центральную точку, или "фокус". (Для геометрического доказательства щелкните Вот.) Поскольку таким образом могут отражаться многие типы энергии, параболические отражатели могут использоваться для сбора и концентрации энергии, попадающей в отражатель под определенным углом. Точно так же энергия, излучаемая от фокуса к тарелке, может передаваться наружу в виде луча, параллельного оси тарелки.
По сравнению с сферические отражатели, которые страдают от сферическая аберрация которая становится сильнее по мере увеличения отношения диаметра луча к фокусному расстоянию, параболические отражатели могут быть изготовлены для размещения лучей любой ширины. Однако, если входящий луч образует ненулевой угол с осью (или если излучающий точечный источник не помещен в фокус), параболические отражатели страдают от аберрация называется кома. Это в первую очередь представляет интерес для телескопов, потому что для большинства других приложений не требуется резкое разрешение вне оси параболы.
Точность, с которой должна быть изготовлена параболическая тарелка, чтобы хорошо фокусировать энергию, зависит от длины волны энергии. Если тарелка отклонена на четверть длины волны, то отраженная энергия будет неверной на половину длины волны, что означает, что она будет разрушительно мешать энергии, которая была должным образом отражена от другой части тарелки. Чтобы этого не произошло, блюдо нужно приготовить правильно с точностью до 1/20 длины волны. Диапазон длин волн видимого света составляет примерно от 400 до 700 нанометров (нм), поэтому для того, чтобы хорошо сфокусировать весь видимый свет, отражатель должен быть правильно настроен с точностью до 20 нм. Для сравнения: диаметр человеческого волоса обычно составляет около 50 000 нм, поэтому требуемая точность отражателя для фокусировки видимого света примерно в 2500 раз меньше диаметра волоса. Например, недостаток в Космический телескоп Хаббла зеркало (слишком плоское примерно на 2200 нм по периметру) вызвало серьезные сферическая аберрация пока не будет исправлено COSTAR.[2]
Микроволны, такие как используемые для сигналов спутникового телевидения, имеют длину волны порядка десяти миллиметров, поэтому тарелки для фокусировки этих волн могут ошибаться на полмиллиметра или около того, но при этом работать хорошо.
Вариации
Сбалансированный рефлектор

Иногда бывает полезно, если центр масс отражателя совпадает с его фокус. Это позволяет легко поворачивать его так, чтобы его можно было направить на движущийся источник света, например на Солнце в небе, в то время как его фокус в месте расположения цели остается неподвижным. Блюдо вращается вокруг топоры которые проходят через фокус и вокруг которых он уравновешен. Если блюдо симметричный и изготовлены из однородного материала постоянной толщины, и если F представляет собой фокусное расстояние параболоида, это условие «сбалансированного фокуса» возникает, если глубина антенны, измеренная вдоль оси параболоида от вершины до плоскости обод блюда, в 1,8478 раза F. Радиус обода 2,7187F.[а] Угловой радиус обода, если смотреть из точки фокусировки, составляет 72,68 градуса.
Отражатель Шеффлера
Конфигурация со сбалансированным фокусом (см. Выше) требует, чтобы глубина тарелки рефлектора была больше ее фокусного расстояния, поэтому фокус находится внутри тарелки. Это может затруднить доступ к фокусу. Альтернативный подход иллюстрируется Отражатель Шеффлера, названный в честь его изобретателя, Вольфганг Шеффлер. Это параболоидальное зеркало, которое вращается вокруг осей, проходящих через его центр масс, но оно не совпадает с фокусом, который находится вне тарелки. Если бы отражатель был жестким параболоидом, фокус двигался бы при повороте антенны. Чтобы избежать этого, рефлектор является гибким и изгибается при вращении, чтобы фокусировка оставалась неподвижной. В идеале рефлектор всегда был бы точно параболоидальным. На практике это не может быть достигнуто точно, поэтому отражатель Шеффлера не подходит для целей, требующих высокой точности. Он используется в таких приложениях, как солнечная кулинария, где солнечный свет должен быть достаточно хорошо сфокусирован, чтобы попасть в кастрюлю, но не в точную точку.[3]
Внеосевые отражатели
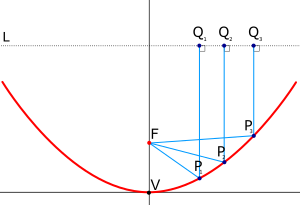
Круговой параболоид теоретически неограничен в размерах. В любом практичном отражателе используется только его часть. Часто сегмент включает вершина параболоида, где его кривизна самый большой, и где ось симметрии пересекает параболоид. Однако, если отражатель используется для фокусировки поступающей энергии на приемник, тень приемника падает на вершину параболоида, который является частью отражателя, поэтому часть отражателя расходуется впустую. Этого можно избежать, сделав отражатель из сегмента параболоида, который смещен от вершины и оси симметрии. Например, на приведенной выше диаграмме отражателем может быть просто часть параболоида между точками P1 и P3. Приемник по-прежнему находится в фокусе параболоида, но он не отбрасывает тень на отражатель. Весь отражатель получает энергию, которая затем фокусируется на приемнике. Это часто делается, например, в приемных антеннах спутникового телевидения, а также в некоторых типах астрономических телескопов (например, то Телескоп Грин-Бэнк).
Точные внеосевые отражатели для использования в солнечные печи и других некритичных приложений, можно довольно просто сделать, используя вращающаяся печь, в котором емкость с расплавленным стеклом смещена относительно оси вращения. Чтобы сделать менее точные, подходящие в качестве спутниковых антенн, форма проектируется компьютером, а затем из листового металла штампуются несколько тарелок.
Внеосевые отражатели, идущие от среды широты к геостационарный спутниковый ТВ где-то выше экватора стоят круче коаксиального рефлектора. В результате рычаг, удерживающий блюдо, может быть короче, и снег будет меньше накапливаться в (нижней части) блюда.
История
Принцип параболических отражателей известен с классическая древность, когда математик Диокл описал их в своей книге О горящих зеркалах и доказали, что они фокусируют параллельный луч в точку.[4] Архимед в третьем веке до нашей эры изучал параболоиды в рамках своего исследования гидростатическое равновесие,[5] и это было утверждал что он использовал отражатели, чтобы поджечь римский флот во время Осада Сиракуз.[6] Однако это кажется маловероятным, поскольку это утверждение не упоминается в источниках до II века нашей эры, и Диокл не упоминает об этом в своей книге.[7] Параболические зеркала также изучались физик Ибн Сахл в 10 веке.[8] Джеймс Грегорив его книге 1663 г. Optica Promota (1663), указал, что отражающий телескоп с параболическим зеркалом исправит сферическая аберрация так же хорошо как Хроматическая аберрация видел в преломляющие телескопы. Дизайн, который он придумал, носит его имя: "Григорианский телескоп"; но, по его собственному признанию, Грегори не обладал практическими навыками, и он не мог найти оптика, способного на самом деле сконструировать такой.[9] Исаак Ньютон знал о свойствах параболических зеркал, но выбрал сферическую форму для своего Ньютоновский телескоп зеркало для упрощения конструкции.[10] Маяки также часто используемые параболические зеркала для объединения точки света от фонаря в луч, прежде чем они будут заменены более эффективными Линзы Френеля в 19 веке. В 1888 г. Генрих Герц, немецкий физик, сконструировал первую в мире параболическую рефлекторную антенну.[11]
Приложения
Наиболее распространенные современные применения параболического отражателя: Спутниковые тарелки, отражающие телескопы, радиотелескопы, параболические микрофоны, солнечные плиты, и много освещение такие устройства, как прожекторы, автомобильные фары, Лампы PAR и корпуса светодиодов.[13]
В Олимпийский огонь традиционно горит на Олимпия, Греция, используя параболический отражатель, концентрирующий Солнечный свет, а затем транспортируется к месту проведения Игр. Параболические зеркала - одна из многих форм для горящее стекло.
Параболические отражатели популярны для использования при создании оптические иллюзии. Они состоят из двух противоположных параболических зеркал с отверстием в центре верхнего зеркала. Когда объект помещается на нижнее зеркало, зеркала создают реальное изображение, который является практически идентичной копией оригинала, изображенного в открытии. Качество изображения зависит от точности оптики. Некоторые из таких иллюзий изготавливаются с точностью до миллионных долей дюйма.
Параболический отражатель, направленный вверх, может быть сформирован путем вращения отражающей жидкости, такой как ртуть, вокруг вертикальной оси. Это делает жидкостный зеркальный телескоп возможный. Та же техника используется в вращающиеся печи сделать сплошные отражатели.
Параболические отражатели также являются популярной альтернативой для увеличения мощности беспроводного сигнала. Даже с простыми, пользователи сообщили о 3 дБ или больше прибыли.[14][15]
Смотрите также
- Джон Д. Краус
- Жидкозеркальный телескоп, параболоиды, полученные вращением
- Параболическая антенна
- Параболический желоб
- Солнечная печь
- Тороидальный отражатель
Сноски
- ^ Близость этого числа к значению «е», основанию натурального логарифма, является просто случайным совпадением, но это действительно полезная мнемоника.
Рекомендации
- ^ Фитцпатрик, Ричард (14 июля 2007 г.). «Сферические зеркала». Farside.ph.utexas.edu. Получено 2012-11-08.
- ^ «Обслуживающая миссия 1». НАСА. Архивировано из оригинал 20 апреля 2008 г.. Получено 26 апреля, 2008.
- ^ Администратор. "Отражатель Шеффлера". www.solare-bruecke.org.
- ^ стр. 162–164, Аполлоний из Коники Перги: текст, контекст, подтекст, Майкл Н. Фрид и Сабетай Унгуру, Брилл, 2001, ISBN 90-04-11977-9.
- ^ стр. 73–74, Забытая революция: как зародилась наука в 300 г. до н.э. и почему ей пришлось возродиться, Лучио Руссо, Биркхойзер, 2004, ISBN 3-540-20068-1.
- ^ «Оружие Архимеда». Журнал Тайм. 26 ноября 1973 г.. Получено 2007-08-12.
- ^ п. 72, Геометрия горящих зеркал в древности, Уилбур Норр, Исида 74 № 1 (март 1983 г.), стр. 53–73, Дои:10.1086/353176.
- ^ С. 465, 468, 469, Пионер в анакластике: Ибн Сал о горящих зеркалах и линзах, Рошди Рашед, Исида, 81, № 3 (сентябрь 1990 г.), стр. 464–491, Дои:10.1086/355456.
- ^ Чемберс, Роберт (1875). Биографический словарь выдающихся шотландцев. Оксфордский университет. п.175.
- ^ Маклин, Ян С. (29 июля 2008 г.). Электронная визуализация в астрономии: детекторы и приборы. Google Книги. ISBN 9783540765820. Получено 2012-11-08.
- ^ «Предыстория радиоастрономии». www.nrao.edu.
- ^ «ALMA удваивает свою мощность на новом этапе более сложных наблюдений». Объявление ESO. Получено 11 января 2013.
- ^ Фитцпатрик, Ричард (14 июля 2007 г.). «Сферические зеркала». Farside.ph.utexas.edu. Получено 2012-11-08.
- ^ «Параболический отражатель, бесплатный усилитель Wi-Fi». Самостоятельное обновление беспроводных антенн и ресурсный центр Wi-Fi | Вопросы и ответы по беспроводной сети WiFi. Binarywolf.com. 2009-08-26. Архивировано из оригинал на 2019-06-09. Получено 2012-11-08.
- ^ "Слайд-шоу: Wi-Fi перестрелка в пустыне". Проводной. 2004-08-03. Получено 2012-11-08.