WikiDer > Передискретизация Ланцоша
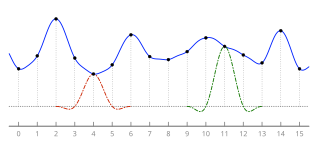
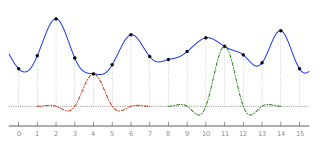
Ланцош фильтрация и Передискретизация по Ланцошу два приложения математической формулы. Его можно использовать как фильтр нижних частот или привык гладко интерполировать ценность цифровой сигнал между его образцы. В последнем случае он отображает каждую выборку данного сигнала на переведенную и масштабированную копию Ядро Ланцоша, что является функция sinc оконный центральной долей второй, более длинной функции sinc. Сумма этих переведенных и масштабированных ядер затем оценивается в желаемых точках.
Передискретизация Ланцоша обычно используется для увеличения частота выборки цифрового сигнала или сдвинуть его на долю интервала дискретизации. Часто используется также для многомерная интерполяция, например, чтобы изменить размер или вращать а цифровое изображение. Он считается «лучшим компромиссом» среди нескольких простых фильтров для этой цели.[1]
Фильтр назван в честь его изобретателя, Корнелиус Ланцош (Венгерское произношение:[ˈLaːnt͡soʃ]).
Определение
Ядро Ланцоша
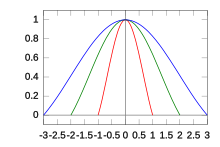
Влияние каждой входной выборки на интерполированные значения определяется фильтром ядро реконструкции L(Икс), называемое ядром Ланцоша. Это нормализованный грех функция sinc (Икс), оконный (умноженное) на Окно Ланцоша, или окно sinc, который является центральным лепестком горизонтально растянутой функции sinc sinc (Икс/а) для −а ≤ Икс ≤ а.
Эквивалентно,
Параметр а - положительное целое число, обычно 2 или 3, которое определяет размер ядра. Ядро Ланцоша имеет 2а − 1 доли: положительный в центре, и а − 1 чередование отрицательных и положительных долей с каждой стороны.
Формула интерполяции
Учитывая одномерный сигнал с выборками sя, для целых значений я, Значение S(Икс) интерполированный при произвольном действительном аргументе Икс получается дискретным свертка из этих образцов с ядром Ланцоша:[2]
где а - параметр размера фильтра, а это функция пола. Границы этой суммы таковы, что вне них ядро равно нулю.
Свойства
Пока параметр а - натуральное число, ядро Ланцоша равно непрерывный везде, и его производная определен и непрерывен всюду (даже при Икс = ±а, где обе функции sinc обращаются в ноль). Следовательно, восстановленный сигнал S(Икс) тоже будет непрерывным, с непрерывной производной.
Ядро Ланцоша равно нулю при каждом целочисленном аргументе Икс, кроме Икс = 0, где он имеет значение 1. Следовательно, восстановленный сигнал точно интерполирует данные отсчеты: мы будем иметь S(Икс) = sя для каждого целочисленного аргумента Икс = я.
Многомерная интерполяция
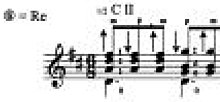
Ядро фильтра Ланцоша в двух измерениях
Оценка
Преимущества

Теоретически оптимальный фильтр реконструкции для ограниченные по полосе сигналы это sinc фильтр, который имеет бесконечное поддержка. Фильтр Ланцоша является одним из многих практических (с конечной поддержкой) приближений фильтра sinc. Каждое интерполированное значение представляет собой взвешенную сумму 2а последовательные входные образцы. Таким образом, варьируя 2а Параметр можно обменять скорость вычислений на улучшенную частотную характеристику. Параметр также позволяет выбирать между более плавной интерполяцией или сохранением резких переходных процессов в данных. Для обработки изображений компромисс между уменьшением сглаживание артефакты и сохранение острых краев. Также, как и при любой такой обработке, нет результатов для границ изображения. Увеличение длины ядра увеличивает обрезку краев изображения.
Фильтр Ланцоша сравнивали с другими методами интерполяции дискретных сигналов, особенно с другими оконными версиями синк-фильтра. Турковский и Габриэль утверждал, что фильтр Ланцоша (с а = 2) «лучший компромисс с точки зрения уменьшения наложения спектров, резкости и минимального звона» по сравнению с усеченным sinc и Бартлетт, косинус-, и Ганна-окна sinc для прореживания и интерполяции данных двумерного изображения.[1] Согласно с Джим Блинн, ядро Ланцоша (с а = 3) «сохраняет низкие частоты и отклоняет высокие частоты лучше, чем любой (достижимый) фильтр, который мы видели до сих пор».[3]
Интерполяция Ланцоша - популярный фильтр для "апскейлинга" видео в различных медиа-утилитах, таких как AviSynth[4] и FFmpeg.[5]
Ограничения
Поскольку ядро принимает отрицательные значения для а > 1, интерполированный сигнал может быть отрицательным, даже если все отсчеты положительны. В более общем смысле, диапазон значений интерполированного сигнала может быть шире, чем диапазон, охватываемый дискретными значениями выборки. В частности, может быть звенящие артефакты непосредственно до и после резких изменений значений выборки, которые могут привести к обрезка артефактов. Однако эти эффекты уменьшены по сравнению с (без оконным) фильтром sinc. Для а = 2 (трехлопастное ядро) звонкость <1%.
Этот метод является одной из опций интерполяции, доступных в бесплатном программном обеспечении GNU Image Manipulation Program (GIMP). Один из способов визуализировать эффект звона - изменить масштаб черно-белого графического блока и выбрать интерполяцию Ланцоша.
При использовании фильтра Ланцоша для передискретизации изображения эффект звона будет создавать светлые и темные ореолы вдоль любых сильных краев. Хотя эти полосы могут визуально раздражать, они помогают увеличить воспринимаемая резкость, и, следовательно, предоставить форму улучшение края. Это может улучшить субъективное качество изображения, учитывая особую роль резкости краев в видение.[6]
В некоторых приложениях артефакты отсечения нижнего уровня могут быть улучшены путем преобразования данных в логарифмическую область до фильтрации. В этом случае интерполированные значения будут средневзвешенным геометрическим, а не средним арифметическим входных выборок.
Ядро Ланцоша не имеет разделение единства свойство. То есть сумма всех копий ядра, переведенных в целое число, не всегда равно 1. Следовательно, интерполяция Ланцоша дискретного сигнала с постоянными выборками не дает постоянной функции. Этот дефект наиболее очевиден, когдаа = 1. Также для а = 1 интерполированный сигнал имеет нулевую производную при каждом целочисленном аргументе. Это довольно академично, поскольку при использовании однополюсного ядра (а = 1) теряет все преимущества подхода Ланцоша и обеспечивает плохой фильтр. Есть много лучших оконных функций в форме колокольчика.
Смотрите также
- Бикубическая интерполяция
- Билинейная интерполяция
- Сплайн-интерполяция
- Интерполяция ближайшего соседа
- Sinc фильтр
использованная литература
- ^ а б Турковски, Кен; Габриэль, Стив (1990). «Фильтры для общих задач передискретизации». В Гласснер, Эндрю С. (ред.). Самоцветы графики I. Академическая пресса. С. 147–165. CiteSeerX 10.1.1.116.7898. ISBN 978-0-12-286165-9.
- ^ Бургер, Вильгельм; Бердж, Марк Дж. (2009). Принципы обработки цифровых изображений: основные алгоритмы. Springer. С. 231–232. ISBN 978-1-84800-194-7.
- ^ Блинн, Джим (1998). Уголок Джима Блинна: грязные пиксели. Морган Кауфманн. С. 26–27. ISBN 978-1-55860-455-1.
- ^ "Изменить размер". Avisynth. 2015-01-01. Получено 2015-07-27.
- ^ «Практическое руководство: повышающее преобразование видео с помощью FFDShow - форумы Neowin». Neowin.net. 2006-04-18. Получено 2012-07-31.
- ^ «IPOL: линейные методы интерполяции изображений». Ipol.im. 2011-09-27. Получено 2012-07-31.
внешние ссылки
- Примеры Anti-Grain Geometry: image_filters.cpp показывает сравнение многократной передискретизации изображения с различными ядрами.
- imageresampler: Общедоступный класс передискретизации изображений в C ++ с поддержкой нескольких оконных ядер фильтра Ланцоша.