WikiDer > Список моментов инерции

List of moments of inertia

Момент инерции, обозначаемый $я$ , измеряет степень сопротивления объекта вращательное ускорение Об конкретная ось, и является вращательным аналогом масса (что определяет устойчивость объекта к линейный ускорение). Массовые моменты инерции имеют единицы из измерение ML²([масса] × [длина]²). Не следует путать с второй момент площади, который используется при расчетах балок. Момент инерции массы часто называют моментом инерции. инерция вращения, а иногда как угловая масса.

Для простых объектов с геометрической симметрией часто можно точно определить момент инерции. выражение в закрытой форме. Обычно это происходит, когда плотность вещества постоянна, но в некоторых случаях плотность может также меняться по всему объекту. В общем, может быть непросто символически выразить момент инерции форм с более сложным распределением масс и отсутствием симметрии. При вычислении моментов инерции полезно помнить, что это аддитивная функция, и использовать параллельная ось и теоремы о перпендикулярной оси.

В этой статье в основном рассматриваются симметричные распределения массы с постоянной плотностью по всему объекту, а ось вращения берется через центр массы если не указано иное.

Моменты инерции

Ниже приведены скалярные моменты инерции. В общем, момент инерции - это тензор, Смотри ниже.

Описание	Фигура	Момент (ы) инерции
Точечная масса M На расстоянии р от оси вращения. Точечная масса не имеет момента инерции вокруг своей оси, но использует теорема о параллельной оси достигается момент инерции вокруг удаленной оси вращения.		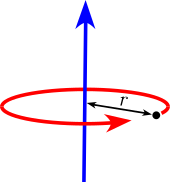${ displaystyle I = мистер ^ {2}}$
Две точечные массы, м₁ и м₂, с уменьшенная масса μ и разделены расстоянием Икс, вокруг оси, проходящей через центр масс системы и перпендикулярной линии, соединяющей две частицы.		${ displaystyle I = { frac {m_ {1} m_ {2}} {m_ {1} ! + ! m_ {2}}} x ^ {2} = mu x ^ {2}}$
стержень длины L и масса м, вращаясь вокруг своего центра. Это выражение предполагает, что стержень представляет собой бесконечно тонкую (но жесткую) проволоку. Это частный случай тонкой прямоугольной пластины с осью вращения в центре пластины, с ш = L и час = 0.		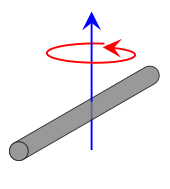${ displaystyle I _ { mathrm {center}} = { frac {1} {12}} mL ^ {2} , !}$ ^[1]
стержень длины L и масса м, вращаясь вокруг одного конца. Это выражение предполагает, что стержень представляет собой бесконечно тонкую (но жесткую) проволоку. Это также частный случай тонкой прямоугольной пластины с осью вращения на конце пластины, с час = L и ш = 0.		${ displaystyle I _ { mathrm {end}} = { frac {1} {3}} mL ^ {2} , !}$ ^[1]
Тонкая круговая петля радиуса р и масса м. Это частный случай тор за а = 0 (см. Ниже), а также толстостенной цилиндрической трубы с открытыми концами с р₁ = р₂ и час = 0.		${ displaystyle I_ {z} = мистер ^ {2} !}$ ${ Displaystyle I_ {x} = I_ {y} = { frac {1} {2}} г-н ^ {2} , !}$
Тонкий, прочный диск радиуса р и масса м. Это частный случай твердого цилиндра с час = 0. Это ${ displaystyle I_ {x} = I_ {y} = { frac {I_ {z}} {2}} ,}$ является следствием теорема о перпендикулярной оси.		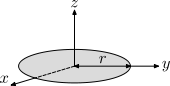${ displaystyle I_ {z} = { frac {1} {2}} мистер ^ {2} , !}$ ${ Displaystyle I_ {x} = I_ {y} = { frac {1} {4}} г-н ^ {2} , !}$
Равномерный диск вокруг оси, перпендикулярной его краю.		${ displaystyle I = { frac {3} {2}} г-н ^ {2}}$ ^[2]
Тонкий однородный диск радиуса р₂ и масса м с круглым отверстием радиуса р₁ о его центре.		${ displaystyle I = { frac {1} {2}} m (r_ {1} ^ {2} + r_ {2} ^ {2})}$
Тонкий цилиндрический оболочка с открытыми концами, радиуса р и масса м. Это выражение предполагает, что толщиной оболочки можно пренебречь. Это частный случай толстостенной цилиндрической трубы для р₁ = р₂.Также точечная масса м на конце стержня длины р имеет тот же момент инерции и значение р называется радиус вращения.		${ Displaystyle I приблизительно г-н ^ {2} , !}$ ^[1]
Сплошной цилиндр радиуса р, высота час и масса м. Это частный случай толстостенной цилиндрической трубы, с р₁ = 0.		${ displaystyle I_ {z} = { frac {1} {2}} мистер ^ {2} , !}$ ^[1] ${ displaystyle I_ {x} = I_ {y} = { frac {1} {12}} m left (3r ^ {2} + h ^ {2} right)}$
Толстостенная цилиндрическая труба с открытыми концами внутреннего радиуса р₁, внешний радиус р₂, длина час и масса м.		${ displaystyle I_ {z} = { frac {1} {2}} m left (r_ {2} ^ {2} + r_ {1} ^ {2} right) = mr_ {2} ^ {2 } left (1-t + { frac {t ^ {2}} {2}} right)}$ ^[1]^[3] куда т = (р₂ - г₁)/р₂ - нормализованное отношение толщины; ${ displaystyle I_ {x} = I_ {y} = { frac {1} {12}} m left (3 left (r_ {2} ^ {2} + r_ {1} ^ {2} right ) + h ^ {2} right)}$ Вышеупомянутая формула предназначена для плоскости xy, находящейся в середине цилиндра. Если плоскость xy находится в основании цилиндра, применяется следующая формула: ${ displaystyle I_ {x} = I_ {y} = { frac {1} {12}} m left (3 left (r_ {2} ^ {2} + r_ {1} ^ {2} right ) + 4h ^ {2} right)}$
Плотностью ρ и та же геометрия примечание: это для объекта с постоянной плотностью		${ displaystyle I_ {z} = { frac { pi rho h} {2}} left (r_ {2} ^ {4} -r_ {1} ^ {4} right)}$ ${ displaystyle I_ {x} = I_ {y} = { frac { pi rho h} {12}} left (3 (r_ {2} ^ {4} -r_ {1} ^ {4}) + h ^ {2} (r_ {2} ^ {2} -r_ {1} ^ {2}) right)}$
Обычный тетраэдр стороны s и масса м		${ displaystyle I _ { mathrm {solid}} = { frac {1} {20}} мс ^ {2} , !}$ ${ displaystyle I _ { mathrm {hollow}} = { frac {1} {12}} мс ^ {2} , !}$ ^[4]
Обычный октаэдр стороны s и масса м		${ displaystyle I_ {x, mathrm {hollow}} = I_ {y, mathrm {hollow}} = I_ {z, mathrm {hollow}} = { frac {1} {6}} мс ^ {2 } , !}$ ^[4] ${ displaystyle I_ {x, mathrm {solid}} = I_ {y, mathrm {solid}} = I_ {z, mathrm {solid}} = { frac {1} {10}} мс ^ {2 } , !}$ ^[4]
Обычный додекаэдр стороны s и масса м		${ displaystyle I_ {x, mathrm {hollow}} = I_ {y, mathrm {hollow}} = I_ {z, mathrm {hollow}} = { frac {39 phi +28} {90}} мс ^ {2}}$ ${ displaystyle I_ {x, mathrm {solid}} = I_ {y, mathrm {solid}} = I_ {z, mathrm {solid}} = { frac {39 phi +28} {150}} мс ^ {2} , !}$ (куда ${ displaystyle phi = { frac {1 + { sqrt {5}}} {2}}}$ ) ^[4]
Обычный икосаэдр стороны s и масса м		${ displaystyle I_ {x, mathrm {hollow}} = I_ {y, mathrm {hollow}} = I_ {z, mathrm {hollow}} = { frac { phi ^ {2}} {6} } мс ^ {2}}$ ${ displaystyle I_ {x, mathrm {solid}} = I_ {y, mathrm {solid}} = I_ {z, mathrm {solid}} = { frac { phi ^ {2}} {10} } мс ^ {2} , !}$ ^[4]
Пустой сфера радиуса р и масса м. Полую сферу можно представить как состоящую из двух стопок бесконечно тонких круглых обручей с радиусом от 0 до р (или один стек, радиус которого отличается от -р к р).		${ displaystyle I = { frac {2} {3}} г-н ^ {2} , !}$ ^[1]
Твердая сфера (мяч) радиуса р и масса м. Сфера может быть взята из двух стопок бесконечно тонких твердых дисков, радиус которых отличается от 0 до р (или один стек, радиус которого отличается от -р к р).		${ displaystyle I = { frac {2} {5}} г-н ^ {2} , !}$ ^[1]
Сфера (оболочка) радиуса р₂ и масса м, с центрированной сферической полостью радиуса р₁. Когда радиус полости р₁ = 0, объект представляет собой сплошной шар (см. Выше). Когда р₁ = р₂, ${ displaystyle left ({ frac {r_ {2} ^ {5} -r_ {1} ^ {5}} {r_ {2} ^ {3} -r_ {1} ^ {3}}} right ) = { frac {5} {3}} r_ {2} ^ {2}}$ , а объект - полая сфера.		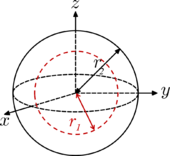${ displaystyle I = { frac {2} {5}} m left ({ frac {r_ {2} ^ {5} -r_ {1} ^ {5}} {r_ {2} ^ {3}) -r_ {1} ^ {3}}} right) , !}$ ^[1]
Правильно круговой конус с радиусом р, высота час и масса м		${ displaystyle I_ {z} = { frac {3} {10}} г-н ^ {2} , !}$ ^[5] Об оси, проходящей через наконечник: ${ displaystyle I_ {x} = I_ {y} = m left ({ frac {3} {20}} r ^ {2} + { frac {3} {5}} h ^ {2} right ) , !}$ ^[5] Об оси, проходящей через основание: ${ displaystyle I_ {x} = I_ {y} = m left ({ frac {3} {20}} r ^ {2} + { frac {1} {10}} h ^ {2} right ) , !}$ Об оси, проходящей через центр масс: ${ displaystyle I_ {x} = I_ {y} = m left ({ frac {3} {20}} r ^ {2} + { frac {3} {80}} h ^ {2} right ) , !}$
Правильно круговой полый конус с радиусом р, высота час и масса м		${ displaystyle I_ {z} = { frac {1} {2}} мистер ^ {2} , !}$ ^[5] ${ displaystyle I_ {x} = I_ {y} = { frac {1} {4}} m left (r ^ {2} + 2h ^ {2} right) , !}$ ^[5]
Тор с малым радиусом а, большой радиус б и масса м.		Об оси, проходящей через центр и перпендикулярной диаметру: ${ displaystyle { frac {1} {4}} m left (4b ^ {2} + 3a ^ {2} right)}$ ^[6] О диаметре: ${ displaystyle { frac {1} {8}} m left (5a ^ {2} + 4b ^ {2} right)}$ ^[6]
Эллипсоид (сплошной) полуосей а, б, и c с массой м		${ displaystyle I_ {a} = { frac {1} {5}} m left (b ^ {2} + c ^ {2} right) , !}$ ${ displaystyle I_ {b} = { frac {1} {5}} m left (a ^ {2} + c ^ {2} right) , !}$ ${ displaystyle I_ {c} = { frac {1} {5}} m left (a ^ {2} + b ^ {2} right) , !}$
Тонкая прямоугольная пластина высотой час, ширина ш и масса м (Ось вращения на конце пластины)		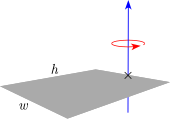${ displaystyle I_ {e} = { frac {1} {12}} m left (4h ^ {2} + w ^ {2} right) , !}$
Тонкая прямоугольная пластина высотой час, ширина ш и масса м (Ось вращения в центре)		${ displaystyle I_ {c} = { frac {1} {12}} m left (h ^ {2} + w ^ {2} right) , !}$ ^[1]
Тонкая прямоугольная пластина радиуса р^[а] и масса м (Ось вращения вдоль боковой стороны пластины)		${ displaystyle I = { frac {1} {3}} г-н ^ {2}}$
Твердый кубовид высоты час, ширина ш, и глубина d, а масса м. Для аналогично ориентированного куб со сторонами длины ${ displaystyle s}$ , ${ displaystyle I _ { mathrm {CM}} = { frac {1} {6}} мс ^ {2} , !}$		${ displaystyle I_ {h} = { frac {1} {12}} m left (w ^ {2} + d ^ {2} right)}$ ${ displaystyle I_ {w} = { frac {1} {12}} m left (d ^ {2} + h ^ {2} right)}$ ${ displaystyle I_ {d} = { frac {1} {12}} m left (w ^ {2} + h ^ {2} right)}$
Твердый кубовид высоты D, ширина W, и длина L, а масса м, вращаясь по самой длинной диагонали. Для куба со сторонами ${ displaystyle s}$ , ${ displaystyle I = { frac {1} {6}} мс ^ {2} , !}$ .		${ displaystyle I = { frac {1} {6}} m left ({ frac {W ^ {2} D ^ {2} + D ^ {2} L ^ {2} + W ^ {2}) L ^ {2}} {W ^ {2} + D ^ {2} + L ^ {2}}} right)}$
Наклонное твердое тело кубовид глубины d, ширина ш, и длина л, а масса м, вращаясь вокруг вертикальной оси (ось y, как показано на рисунке). Для куба со сторонами 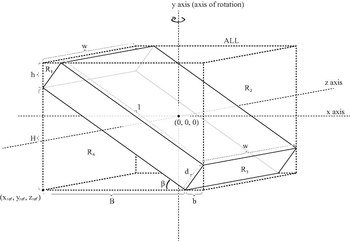${ displaystyle s}$ , ${ displaystyle I = { frac {1} {6}} мс ^ {2} , !}$ .		${ displaystyle I = { frac {m} {12}} left (l ^ {2} cos ^ {2} beta + d ^ {2} sin ^ {2} beta + w ^ {2 }верно)}$ ^[7]
Треугольник с вершинами в начале координат и в точке п и Q, с массой м, вращающейся вокруг оси, перпендикулярной плоскости, и проходящей через начало координат.		${ Displaystyle I = { гидроразрыва {1} {6}} м ( mathbf {P} cdot mathbf {P} + mathbf {P} cdot mathbf {Q} + mathbf {Q} cdot mathbf {Q})}$
Самолет многоугольник с вершинами п₁, п₂, п₃, ..., п_N и масса м равномерно распределен внутри, вращаясь вокруг оси, перпендикулярной плоскости, и проходящей через начало координат.		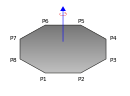${ displaystyle I = m left ({ frac { sum limits _ {n = 1} ^ {N} \| mathbf {P} _ {n + 1} times mathbf {P} _ {n } \| left ( left ( mathbf {P} _ {n} cdot mathbf {P} _ {n} right) + left ( mathbf {P} _ {n} cdot mathbf { P} _ {n + 1} right) + left ( mathbf {P} _ {n + 1} cdot mathbf {P} _ {n + 1} right) right)} {6 sum limits _ {n = 1} ^ {N} \| mathbf {P} _ {n + 1} times mathbf {P} _ {n} \|}} right)}$
Самолет правильный многоугольник с п-вершины и масса м равномерно распределен внутри, вращаясь вокруг оси, перпендикулярной плоскости, и проходящей через его центр масс. р - радиус описанной окружности.		${ displaystyle I = { frac {1} {2}} mR ^ {2} left (1 - { frac {2} {3}} sin ^ {2} left ({ tfrac { pi } {n}} right) right)}$ ^[8]
Равнобедренный треугольник массы M, угол при вершине 2β и общая длина стороны L (ось, проходящая через наконечник, перпендикулярна плоскости)		${ displaystyle I = { frac {1} {2}} mL ^ {2} left (1 - { frac {2} {3}} sin ^ {2} left ( beta right) верно)}$ ^[8]
Бесконечный диск с массой, распределенной в Двумерное распределение Гаусса на двух осях вокруг оси вращения с плотностью массы как функцией вектора положения 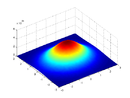${ displaystyle { mathbf {x}}}$ ${ displaystyle rho ({ mathbf {x}}) = m { frac { exp left (- { frac {1} {2}} { mathbf {x}} ^ { mathrm {T}) } { boldsymbol { Sigma}} ^ {- 1} { mathbf {x}} right)} { sqrt {(2 pi) ^ {2} \| { boldsymbol { Sigma}} \|}} }}$		${ Displaystyle I = м cdot OperatorName {tr} ({ boldsymbol { Sigma}}) , !}$

Список трехмерных тензоров инерции

Этот список тензоры момента инерции дается для главные оси каждого объекта.

Чтобы получить скалярные моменты инерции я выше тензорный момент инерции я проецируется вдоль некоторой оси, определяемой единичный вектор п в соответствии с формулой:

{ Displaystyle mathbf {n} cdot mathbf {I} cdot mathbf {n} Equiv n_ {i} I_ {ij} n_ {j} ,,}

где точки указывают тензорное сжатие и Соглашение о суммировании Эйнштейна используется. В приведенной выше таблице п будет единицей Декартова основа е_Икс, е_у, е_z чтобы получить я_Икс, я_у, я_z соответственно.

Описание	Фигура	Момент тензора инерции
Твердый сфера радиуса р и масса м		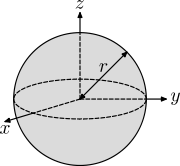${ displaystyle I = { begin {bmatrix} { frac {2} {5}} mr ^ {2} & 0 & 0 0 & { frac {2} {5}} mr ^ {2} & 0 0 & 0 & { frac {2} {5}} мистер ^ {2} end {bmatrix}}}$
Полая сфера радиуса р и масса м		${ displaystyle I = { begin {bmatrix} { frac {2} {3}} mr ^ {2} & 0 & 0 0 & { frac {2} {3}} mr ^ {2} & 0 0 & 0 & { frac {2} {3}} мистер ^ {2} end {bmatrix}}}$
Твердый эллипсоид полуосей а, б, c и масса м		${ displaystyle I = { begin {bmatrix} { frac {1} {5}} m (b ^ {2} + c ^ {2}) & 0 & 0 0 & { frac {1} {5}} m (a ^ {2} + c ^ {2}) & 0 0 & 0 & { frac {1} {5}} m (a ^ {2} + b ^ {2}) end {bmatrix}}}$
Правый круговой конус с радиусом р, высота час и масса м, о вершине		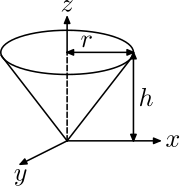${ displaystyle I = { begin {bmatrix} { frac {3} {5}} mh ^ {2} + { frac {3} {20}} mr ^ {2} & 0 & 0 0 & { frac { 3} {5}} mh ^ {2} + { frac {3} {20}} mr ^ {2} & 0 0 & 0 & { frac {3} {10}} mr ^ {2} end {bmatrix }}}$
Сплошной кубоид шириной ш, высота час, глубина d, а масса м		${ displaystyle I = { begin {bmatrix} { frac {1} {12}} m (h ^ {2} + d ^ {2}) & 0 & 0 0 & { frac {1} {12}} m (w ^ {2} + d ^ {2}) & 0 0 & 0 & { frac {1} {12}} m (w ^ {2} + h ^ {2}) end {bmatrix}}}$
Стройный стержень вдоль у-ось длины л и масса м о конце		${ displaystyle I = { begin {bmatrix} { frac {1} {3}} ml ^ {2} & 0 & 0 0 & 0 & 0 0 & 0 & { frac {1} {3}} ml ^ {2} end {bmatrix}}}$
Стройный стержень вдоль у-ось длины л и масса м о центре		${ displaystyle I = { begin {bmatrix} { frac {1} {12}} ml ^ {2} & 0 & 0 0 & 0 & 0 0 & 0 & { frac {1} {12}} ml ^ {2} end {bmatrix}}}$
Сплошной цилиндр радиуса р, высота час и масса м		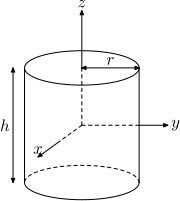${ displaystyle I = { begin {bmatrix} { frac {1} {12}} m (3r ^ {2} + h ^ {2}) & 0 & 0 0 & { frac {1} {12}} m (3r ^ {2} + h ^ {2}) & 0 0 & 0 & { frac {1} {2}} г-н ^ {2} end {bmatrix}}}$
Толстостенная цилиндрическая труба с открытыми концами внутреннего радиуса р₁, внешний радиус р₂, длина час и масса м		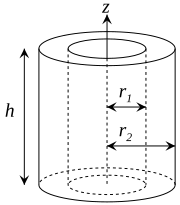${ displaystyle I = { begin {bmatrix} { frac {1} {12}} m (3 (r_ {2} ^ {2} + r_ {1} ^ {2}) + h ^ {2}) & 0 & 0 0 & { frac {1} {12}} m (3 (r_ {2} ^ {2} + r_ {1} ^ {2}) + h ^ {2}) & 0 0 & 0 & { frac {1} {2}} m (r_ {2} ^ {2} + r_ {1} ^ {2}) end {bmatrix}}}$

Смотрите также

внешняя ссылка

Ошибка цитирования: есть <ref group=lower-alpha> теги или {{efn}} шаблоны на этой странице, но ссылки не будут отображаться без {{reflist | group = lower-alpha}} шаблон или {{notelist}} шаблон (см. страница помощи).

[serway-1] а ^б ^c ^d ^е ^ж ^грамм ^час ^я Раймонд А. Сервей (1986). Физика для ученых и инженеров (2-е изд.). Издательство колледжа Сондерс. п.202. ISBN 0-03-004534-7.

[2] Гао, Юнли. «Физика 141 - Механика - Лекция 15 - Момент инерции». Слайд 10: Пример: момент инерции диска относительно края. Архивировано из оригинал на 2015-09-24. Получено 2014-11-23.

[3] Классическая механика - Момент инерции однородного полого цилиндра. В архиве 2007-02-07 в Wayback Machine. LivePhysics.com. Проверено 31 января 2008.

[satterly-4] а ^б ^c ^d ^е Саттерли, Джон (1958). «Моменты инерции некоторых многогранников». Математический вестник. Математическая ассоциация. 42 (339): 11–13. Дои:10.2307/3608345. JSTOR 3608345.

[beer-5] а ^б ^c ^d Фердинанд П. Бир и Э. Рассел Джонстон-младший (1984). Векторная механика для инженеров, четвертое изд.. Макгроу-Хилл. п. 911. ISBN 0-07-004389-2.

[weisstein_torus-6] а ^б Эрик В. Вайсштейн. «Момент инерции - кольцо». Wolfram Research. Получено 2016-12-14.

[8] А. Панагопулос и Г. Халкиадакис. Момент инерции потенциально наклонных кубоидов. Технический отчет, Саутгемптонский университет, 2015 г.

[six-9] а ^б Дэвид Морин (2010). Введение в классическую механику: с проблемами и решениями; первое издание (8 января 2010 г.). Издательство Кембриджского университета. п.320. ISBN 978-0521876223.

[1]

[2]

[3]

[4]

[5]

[6]

[а]

[7]

[8]

Navigation

Navigation

Themenportale

WikiDer > Список моментов инерции

Содержание

Моменты инерции

Список трехмерных тензоров инерции

Смотрите также

Рекомендации

внешняя ссылка