WikiDer > Метод Нелдера – Мида

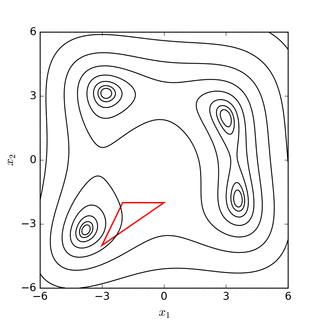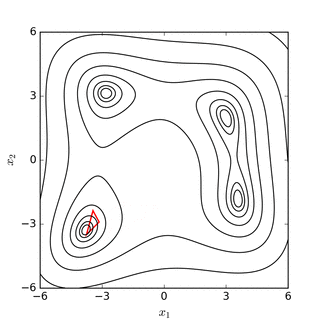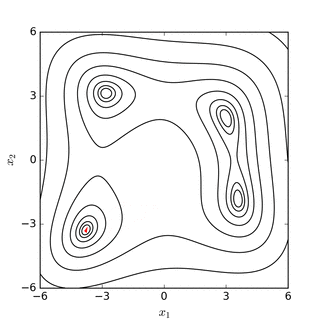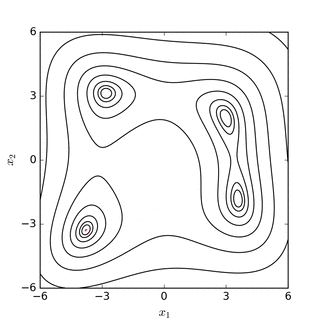Симплексный поиск Нелдера – Мида по Розенброк банановая функция(над) и Функция Химмельблау (ниже)

Минимальный поиск Нелдера – Мида Функция Симионеску. Вершины симплекса упорядочены по их значению, причем 1 имеет наименьшее (лучшее) значение.

В Метод Нелдера – Мида (также односторонний спуск, метод амебы, или же многогранник) широко применяется численный метод используется для нахождения минимума или максимума целевая функция в многомерном пространстве. Это метод прямого поиска (основан на сравнении функций) и часто применяется к нелинейным оптимизация проблемы, для которых производные могут быть неизвестны. Однако метод Нелдера – Мида - это эвристический метод поиска, который может сходиться к нестационарным точкам^[1] о проблемах, которые можно решить альтернативными методами.^[2]

Техника Нелдера – Мида была предложена Джон Нелдер и Роджер Мид в 1965 г.,^[3] как развитие метода Spendley et al.^[4]

Обзор

В методе используется концепция симплекс, что является особенным многогранник из п + 1 вершина в п Габаритные размеры. Примеры симплексов включают отрезок на прямой, треугольник на плоскости, тетраэдр в трехмерном пространстве и так далее.

Метод аппроксимирует локальный оптимум задачи с п переменных, когда целевая функция изменяется плавно и одномодальный. Типичные реализации минимизируют функции, а мы максимизируем ${ Displaystyle е ( mathbf {х})}$ минимизируя ${ Displaystyle -f ( mathbf {х})}$.

Например, инженер по подвесному мосту должен выбрать толщину каждой стойки, троса и опоры. Эти элементы взаимозависимы, но непросто представить себе влияние изменения какого-либо конкретного элемента. Моделирование таких сложных структур часто требует чрезвычайно больших вычислительных затрат и, возможно, занимает более часов на выполнение. Метод Нелдера – Мида в исходном варианте требует не более двух вычислений на итерацию, за исключением сокращаться описанная ниже операция, которая привлекательна по сравнению с некоторыми другими методами оптимизации прямого поиска. Однако общее количество итераций до предложенного оптимума может быть большим.

Нелдер – Мид ин п размеры поддерживает набор п + 1 контрольная точка в виде симплекс. Затем он экстраполирует поведение целевой функции, измеренной в каждой контрольной точке, чтобы найти новую контрольную точку и заменить одну из старых контрольных точек на новую, и таким образом методика прогрессирует. Самый простой подход - заменить худшую точку точкой, отраженной через центроид из оставшихся п точки. Если эта точка лучше, чем лучшая текущая точка, мы можем попробовать экспоненциально растянуться вдоль этой линии. С другой стороны, если эта новая точка не намного лучше, чем предыдущее значение, то мы переходим через долину, поэтому мы сжимаем симплекс в сторону лучшей точки. Интуитивное объяснение алгоритма из «Численных рецептов»:^[5]

Симплексный метод спуска теперь включает серию шагов, большинство из которых просто перемещают точку симплекса, где функция наибольшая («самая высокая точка»), через противоположную сторону симплекса в нижнюю точку. Эти шаги называются отражениями, и они построены так, чтобы сохранить объем симплекса (и, следовательно, сохранить его невырожденность). Когда это возможно, метод расширяет симплекс в том или ином направлении, делая более крупные шаги. Когда он достигает «дна долины», метод сжимается в поперечном направлении и пытается просочиться вниз по долине. Если возникает ситуация, когда симплекс пытается «пройти сквозь игольное ушко», он сжимается во всех направлениях, втягиваясь вокруг своей самой нижней (лучшей) точки.

В отличие от современных методов оптимизации, эвристика Нелдера – Мида может сходиться к нестационарной точке, если только задача не удовлетворяет более строгим условиям, чем это необходимо для современных методов.^[1] Современные усовершенствования эвристики Нелдера – Мида известны с 1979 года.^[2]

Существует множество вариаций, зависящих от реальной природы решаемой проблемы. В распространенном варианте используется небольшой симплекс постоянного размера, который примерно следует направлению градиента (что дает крутой спуск). Визуализируйте маленький треугольник на карте высот, переворачивающийся вниз по долине к местному дну. Этот метод также известен как метод гибкого многогранника. Это, однако, имеет тенденцию плохо работать по сравнению с методом, описанным в этой статье, поскольку он выполняет небольшие ненужные шаги в областях, которые не представляют особого интереса.

Один из возможных вариантов алгоритма NM

(Это примерно соответствует процедуре, описанной в исходной статье Нелдера – Мида.)

Метод Нелдера – Мида, примененный к Функция Розенброка

Мы пытаемся минимизировать функцию ${ Displaystyle е ( mathbf {х})}$, куда ${ displaystyle mathbf {x} in mathbb {R} ^ {n}}$. Наши текущие контрольные точки: ${ displaystyle mathbf {x} _ {1}, ldots, mathbf {x} _ {n + 1}}$.

1. Заказать по значениям в вершинах:

${ Displaystyle е ( mathbf {x} _ {1}) leq f ( mathbf {x} _ {2}) leq cdots leq f ( mathbf {x} _ {n + 1}). }$

Проверьте, должен ли метод останавливаться. Видеть Прекращение ниже. Иногда неуместно называют «конвергенцией».

2. Рассчитать ${ displaystyle mathbf {x} _ {o}}$, то центроид всех пунктов, кроме ${ Displaystyle mathbf {х} _ {п + 1}}$.

3. Отражение

Вычислить отраженную точку ${ displaystyle mathbf {x} _ {r} = mathbf {x} _ {o} + alpha ( mathbf {x} _ {o} - mathbf {x} _ {n + 1})}$ с ${ displaystyle alpha> 0}$.

Если отраженная точка лучше второй худшей, но не лучше лучшей, т.е. ${ Displaystyle е ( mathbf {x} _ {1}) leq f ( mathbf {x} _ {r})$,

затем получить новый симплекс, заменив худшую точку ${ Displaystyle mathbf {х} _ {п + 1}}$ с отраженной точкой ${ displaystyle mathbf {x} _ {r}}$и перейдите к шагу 1.

4. Расширение

Если отраженная точка пока лучшая, ${ Displaystyle е ( mathbf {х} _ {г}) <е ( mathbf {х} _ {1})}$,

затем вычислите расширенную точку ${ displaystyle mathbf {x} _ {e} = mathbf {x} _ {o} + gamma ( mathbf {x} _ {r} - mathbf {x} _ {o})}$ с ${ displaystyle gamma> 1}$.

Если расширенная точка лучше отраженной точки, ${ Displaystyle е ( mathbf {х} _ {е}) <е ( mathbf {х} _ {г})}$,

затем получить новый симплекс, заменив худшую точку ${ Displaystyle mathbf {х} _ {п + 1}}$ с расширенной точкой ${ displaystyle mathbf {x} _ {e}}$ и перейти к шагу 1;

иначе получить новый симплекс, заменив худшую точку ${ Displaystyle mathbf {х} _ {п + 1}}$ с отраженной точкой ${ displaystyle mathbf {x} _ {r}}$ и переходите к шагу 1.

5. Сокращение

Здесь несомненно, что ${ Displaystyle е ( mathbf {x} _ {r}) geq f ( mathbf {x} _ {n})}$. (Обратите внимание, что ${ displaystyle mathbf {x} _ {n}}$ является вторым или «ближайшим к высшему».)

Вычислить сокращенную точку ${ displaystyle mathbf {x} _ {c} = mathbf {x} _ {o} + rho ( mathbf {x} _ {n + 1} - mathbf {x} _ {o})}$ с ${ displaystyle 0 < rho leq 0,5}$.

Если сжатая точка лучше худшей, т.е. ${ Displaystyle е ( mathbf {х} _ {с}) <е ( mathbf {x} _ {п + 1})}$,

затем получить новый симплекс, заменив худшую точку ${ Displaystyle mathbf {х} _ {п + 1}}$ со сжатой точкой ${ displaystyle mathbf {x} _ {c}}$ и перейти к шагу 1;

6. Усадка

Заменить все точки кроме лучшего (${ displaystyle mathbf {x} _ {1}}$) с

${ displaystyle mathbf {x} _ {i} = mathbf {x} _ {1} + sigma ( mathbf {x} _ {i} - mathbf {x} _ {1})}$ и переходите к шагу 1.

Примечание: ${ displaystyle alpha}$, ${ displaystyle gamma}$, ${ displaystyle rho}$ и ${ displaystyle sigma}$ являются соответственно коэффициентами отражения, расширения, сжатия и сжатия. Стандартные значения: ${ Displaystyle альфа = 1}$, ${ displaystyle gamma = 2}$, ${ Displaystyle rho = 1/2}$ и ${ Displaystyle sigma = 1/2}$.

Для отражение, поскольку ${ Displaystyle mathbf {х} _ {п + 1}}$ является вершиной с более высоким ассоциированным значением среди вершин, мы можем ожидать найти более низкое значение при отражении ${ Displaystyle mathbf {х} _ {п + 1}}$ на противоположной грани, образованной всеми вершинами ${ Displaystyle mathbf {х} _ {я}}$ Кроме ${ Displaystyle mathbf {х} _ {п + 1}}$.

Для расширение, если точка отражения ${ displaystyle mathbf {x} _ {r}}$ - новый минимум по вершинам, мы можем ожидать найти интересные значения по направлению от ${ displaystyle mathbf {x} _ {o}}$ к ${ displaystyle mathbf {x} _ {r}}$.

Касательно сокращение, если ${ Displaystyle е ( mathbf {x} _ {r})> е ( mathbf {x} _ {n})}$, можно ожидать, что лучшее значение будет внутри симплекса, образованного всеми вершинами ${ Displaystyle mathbf {х} _ {я}}$.

Наконец, сокращаться справляется с редким случаем, когда сокращение от самой большой точки увеличивает ${ displaystyle f}$, то, что не может произойти достаточно близко к неособому минимуму. В этом случае мы приближаемся к самой низкой точке в ожидании более простого ландшафта. Тем не менее, Нэш отмечает, что арифметика конечной точности иногда может не сжимать симплекс, и реализовал проверку того, что размер действительно уменьшается.^[6]

Начальный симплекс

Начальный симплекс важен. Действительно, слишком маленький начальный симплекс может привести к локальному поиску, следовательно, NM может легко застрять. Таким образом, этот симплекс должен зависеть от характера проблемы. Однако в исходной статье предлагался симплекс, в котором начальная точка задается как ${ displaystyle mathbf {x} _ {1}}$, а остальные генерируются с фиксированным шагом по каждому измерению по очереди. Таким образом, метод чувствителен к масштабированию переменных, составляющих ${ displaystyle mathbf {x}}$.

Прекращение

Критерии необходимы, чтобы разорвать итерационный цикл. Нелдер и Мид использовали стандартное отклонение выборки значений функции текущего симплекса. Если они падают ниже некоторого допуска, то цикл останавливается, и самая низкая точка в симплексе возвращается как предложенный оптимум. Обратите внимание, что очень «плоская» функция может иметь почти равные значения функции в большой области, так что решение будет чувствительно к допуску. Нэш добавляет тест на усадку в качестве еще одного критерия завершения.^[6] Обратите внимание, что программы завершаются, а итерации могут сходиться.

Смотрите также

Рекомендации

дальнейшее чтение

• Авриэль, Мардохей (2003). Нелинейное программирование: анализ и методы.. Dover Publishing. ISBN 978-0-486-43227-4.
• Coope, I.D .; Прайс, К. Дж. (2002). «Положительные основы численной оптимизации». Вычислительная оптимизация и приложения. 21 (2): 169–176. Дои:10.1023 / А: 1013760716801. S2CID 15947440.
• Gill, Philip E .; Мюррей, Уолтер; Райт, Маргарет Х. (1981). «Методы многомерных негладких функций». Практическая оптимизация. Нью-Йорк: Academic Press. стр.93–96. ISBN 978-0-12-283950-4.
• Kowalik, J .; Осборн, М. Р. (1968). Методы решения задач неограниченной оптимизации. Нью-Йорк: Эльзевир. стр.24–27. ISBN 0-444-00041-0.
• Суонн, В. Х. (1972). «Методы прямого поиска». В Мюррей, W. (ред.). Численные методы безусловной оптимизации. Нью-Йорк: Academic Press. С. 13–28. ISBN 978-0-12-512250-4.

внешняя ссылка

• Объяснение и визуализация Нелдера – Мида (Downhill Simplex) с функцией банана Розенброка
• Джон Буркардт: код Нелдера – Мида в Matlab - обратите внимание, что вариант метода Нелдера – Мида также реализован функцией Matlab fminsearch.
• Оптимизация Нелдера-Мида в Python в библиотеке SciPy.
• Nelder-Mead - Реализация Python метода Нелдера – Мида.
• SOVA 1.0 (бесплатное ПО) - Симплексная оптимизация для различных приложений
• [1] - HillStormer, практический инструмент для нелинейной, многомерной и линейной симплексной оптимизации с ограничениями от Nelder Mead.