WikiDer > Омнитусеченные 6-симплексные соты - Википедия
| Усеченные 6-симплексные соты | |
|---|---|
| (Нет изображения) | |
| Тип | Равномерные соты |
| Семья | Усеченные простые соты |
| Символ Шлефли | {3[8]} |
| Диаграммы Кокстера – Дынкина | |
| Грани |  т0,1,2,3,4,5{3,3,3,3,3} |
| Фигура вершины | 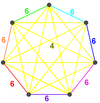 Irr. 6-симплекс |
| Симметрия | ×14, [7[3[7]]] |
| Характеристики | вершинно-транзитивный |
В шестимерный Евклидова геометрия, то усеченные 6-симплексные соты заполняет пространство мозаика (или же соты). Он полностью состоит из омниусеченный 6-симплексный грани.
Грани всего усеченные простые соты называются пермутаэдры и может быть размещен в п + 1 пространство с целыми координатами, перестановками целых чисел (0,1, .., n).
А*
6 решетка
А*
6 решетка (также называемая A7
6) - это объединение семи А6 решетки, и имеет расположение вершин двойного к усеченные 6-симплексные соты, и поэтому Ячейка Вороного этой решетки является омниусеченный 6-симплексный.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() ∪
∪ ![]()
![]()
![]()
![]()
![]()
![]()
![]() = двойной
= двойной ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Связанные многогранники и соты
Эти соты - одна из 17 уникальных однородных сот[1] построенный Группа Коксетера, сгруппированные по их расширенной симметрии Диаграммы Кокстера – Дынкина:
| Соты A6 | ||||
|---|---|---|---|---|
| Семиугольник симметрия | Расширенный симметрия | Расширенный диаграмма | Расширенный группа | Соты |
| а1 | [3[7]] |
| ||
| i2 | [[3[7]]] | ×2 | ||
| r14 | [7[3[7]]] | ×14 | ||
Проекция складыванием
В усеченные 6-симплексные соты можно проецировать в 4-мерное кубические соты по геометрическая складка операция, которая отображает две пары зеркал друг в друга, разделяя одни и те же расположение вершин:
Смотрите также
Регулярные и однородные соты в 6-м пространстве:
Примечания
- ^ * Вайсштейн, Эрик В. "Ожерелье". MathWorld., OEIS последовательность A000029 18-1 случаев, пропуская один с нулевыми отметками
Рекомендации
- Норман Джонсон Равномерные многогранники, Рукопись (1991)
- Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN 978-0-471-01003-6 [1]
- (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Однородные заполнители пространств)
- (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
| Космос | Семья | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Равномерная черепица | {3[3]} | δ3 | hδ3 | qδ3 | Шестиугольный |
| E3 | Равномерно выпуклые соты | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Равномерные 4-соты | {3[5]} | δ5 | hδ5 | qδ5 | 24-ячеечные соты |
| E5 | Равномерные 5-соты | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Равномерные 6-соты | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Равномерные 7-соты | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Равномерные 8-соты | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Равномерные 9-соты | {3[10]} | δ10 | hδ10 | qδ10 | |
| Eп-1 | Униформа (п-1)-соты | {3[n]} | δп | hδп | qδп | 1k2 • 2k1 • k21 |









