WikiDer > Планигон - Википедия

Planigon - Wikipedia

Три правильные многоугольники, 8 планигоны, четыре полуправильных планигона и шесть непригодных для использования планигонных треугольников, которые не могут участвовать в двойных однородных мозаиках; все в масштабе. Они окрашены обратно пропорционально размеру и упорядочены по размеру в каждой категории. Размер всего изображения составляет половину каждой двойной однородной мозаики (2560 × 1280 пикселей).

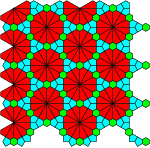
В геометрия, а планигон это выпуклый многоугольник который может заполнить плоскость только своими копиями (которые изотопический к основные единицы из моноэдральная мозаика). На евклидовой плоскости есть 3 правильные формы равносторонний треугольник, квадраты, и правильные шестиугольники; и 8 полурегулярных форм; и 4-полурегулярные формы, которые могут перекрывать плоскость другими планигонами.

Все углы планигона составляют целые 360 °. Замощения образуются соединениями от края до края серединными перпендикулярными ребрам исходной однородной решетки или центроидами по общим ребрам (они совпадают).

Плитки из планигонов можно рассматривать как двойные мозаики к регулярный, полурегулярный, и полурегулярный разбиение плоскости на правильные многоугольники.

История

В книге 1987 г. Плитки и узоры, Бранко Грюнбаум называет однородные по вершинам мозаики Архимедов параллельно с Архимедовы тела. Их двойные мозаики называются Лавес плитки в честь кристаллограф Фриц Лавес.^[1]^[2] Их еще называют Разбиения Шубникова – Лавеса после Шубников Алексей Васильевич.^[3] Джон Конвей называет равномерные дуалы Каталонская мозаика, параллельно с Каталонский твердый многогранники.

У мозаик Лавеса есть вершины в центрах правильных многоугольников и ребра, соединяющие центры правильных многоугольников с общим ребром. В плитка мозаик Лавеса называются планигоны. Сюда входят 3 правильных плитки (треугольник, квадрат и шестиугольник) и 8 неправильных плиток.^[4] У каждой вершины есть ребра, равномерно расположенные вокруг нее. Трехмерные аналоги планигоны называются стереоэдры.

Эти мозаики перечислены по их конфигурация лица, количество граней в каждой вершине грани. Например V4.8.8 (или V4.8²) означает плитки равнобедренных треугольников, в одном углу которых четыре треугольника, а в двух углах - восемь треугольников.

Строительство

В Конвей операция двойных перестановок граней и вершин. В Архимедовы тела и k-однородные мозаики аналогично, новая вершина совпадает с центром каждого обычное лицо, или центроид. В евклидовом (плоском) случае; чтобы создать новые грани вокруг каждой исходной вершины, центроиды должны быть соединены новыми ребрами, каждое из которых должно пересекать ровно одно из исходных ребер. Поскольку правильные многоугольники имеют двугранная симметрия, мы видим, что эти новые грани центроид-центроид должны быть перпендикулярные биссектрисы общих исходных ребер (например, центр тяжести лежит на всех ребрах, перпендикулярных биссектрисам правильного многоугольника). Таким образом, края k-двойные равномерные мозаики совпадают с отрезками средней точки всех правильных многоугольников в k-однородные мозаики.

Итак, мы можем в качестве альтернативы построить k-двойные однородные мозаики (и все 21 планигон) эквивалентно путем формирования новых сегментов средней точки с ребрами центроидов исходных правильных многоугольников (рассекая правильные п-угольники в п конгруэнтные дельтовидные мышцы, орто), а затем удалив исходные края (двойной). Замкнутые планигоны будут формироваться вокруг внутренних вершин, а линейные сегменты (многих возможных) планигонов будут формироваться вокруг граничных вершин, давая точный результат. k-двойная однородная решетка (орто-наложенные и в масштабе). С другой стороны, соединение центроид-центроид дает только внутренние планигоны (с переменным перемещением и масштабом), но эта конструкция, тем не менее, эквивалентна внутри. Если оригинал k- равномерная мозаика заполняет всю рамку, затем k-двойная равномерная решетка по первой конструкции, и отрезки граничных линий можно не учитывать (эквивалент второй конструкции).

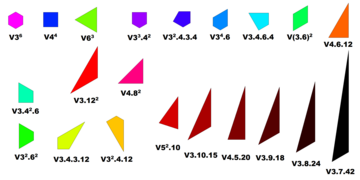
Как видно ниже, некоторые типы вершинных полигонов отличаются от своих зеркальных отображений и перечислены дважды. Например, треугольник ${ Displaystyle треугольник ABC, треугольник CBA}$ зеркальное отображение, если ${ Displaystyle угол А, угол В, угол С}$ все уникальны. На этих изображениях многоугольники вершин перечислены против часовой стрелки справа и закрашены разными цветами с помощью длина волны частота обратная площади. Обратите внимание, 4.8² фиолетово-красный планигон окрашен неуместно, так как не может существовать ни с одним другим планигон в любом k-однородная черепица. Всего существует 29 возможных правильных вершинных многоугольников (21 исключая энантиоморфы): 3 правильные многоугольники, 8 планигоны, 4 полуправильные планигоны, и 6 неиспользуемые полигоны.

Альтернативная конструкция

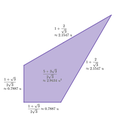
Все 14 произвольных равномерно используемых вершинных регулярных планигонов (VRP) также приветствуют^[5] от 6-5 додекаграмма (где каждый сегмент подчиняется ${ displaystyle 5 pi / 6}$ радианы, или ${ displaystyle 150}$ градусов).

В окружать этой додекаграммы демонстрирует, что все 14 VRP кокциклический, как альтернативно показано окружностью амвонских упаковок. Напоминаем, что отношение вписанной окружности к описанной составляет

${ displaystyle sin { frac { pi} {12}} = sin 15 ^ { circ} = { frac {{ sqrt {6}} - { sqrt {2}}} {4}} приблизительно 0,258819}$

а выпуклая оболочка - это в точности регулярные додекагоны в произвольных равномерных мозаиках! Фактически, равносторонний треугольник, квадрат, правильный шестиугольник и правильный двенадцатигранник; показаны ниже вместе с VRP:

Построение правильных многоугольников и вершинных правильных планигонов произвольных равномерных мозаик из додекаграммы 6-5. Эта додекаграмма имеет края, охватывающие 150 градусов. Есть 4 правильных многоугольника и 14 вершинных правильных планигонов (правильный восьмиугольник и равнобедренный прямоугольный треугольник использовать нельзя).

Вывод всех возможных правильных вершинных многоугольников

Для непрерывных евклидовых мозаик внутренние углы полигонов, пересекающихся в вершине, должно составлять 360 градусов. Обычный $п$ -угольник имеет внутренний угол ${ displaystyle left (1 - { frac {2} {n}} right) 180 ^ { circ}}$ градусов. Существует семнадцать комбинаций правильных многоугольников, внутренние углы которых в сумме составляют 360 градусов, каждая из которых называется разновидность вершины; в четырех случаях есть два различных циклических порядка многоугольников, что дает двадцать один типы вершины.

Фактически с вершинными (внутренними) углами ${ displaystyle 60 ^ { circ}, 90 ^ { circ}, 108 ^ { circ}, 120 ^ { circ}, 128 { frac {4} {7}} ^ { circ}, 135 ^ { circ}, 140 ^ { circ}, 144 ^ { circ}, 147 { frac {3} {11}} ^ { circ}, 150 ^ { circ}, dots}$ , мы можем найти все комбинации допустимых углов угла по следующим правилам: (i) каждая вершина имеет степень не менее 3 (вершина степени 2 должна иметь два прямых угла или один угол отражения); (ii) если вершина имеет степень ${ displaystyle d}$ , наименьший ${ displaystyle d-1}$ сумма углов вершин многоугольника превышает ${ displaystyle 180 ^ { circ}}$ ; (iii) углы при вершинах складываются с ${ displaystyle 360 ^ { circ}}$ , и должны быть углами правильных многоугольников с целыми положительными сторонами (последовательности ${ displaystyle 60 ^ { circ}, 90 ^ { circ}, 108 ^ { circ}, 120 ^ { circ}, 128 { frac {4} {7}} ^ { circ}, 135 ^ { circ}, 140 ^ { circ}, 144 ^ { circ}, 147 { frac {3} {11}} ^ { circ}, 150 ^ { circ}, dots}$ ). Решение задачи 9.46, Геометрия (Рускик), стоит в столбце Степень 3 Вершина ниже.^[6]

Расположение правильных многоугольников вокруг вершины
Степень-6 вершина	Вершина степени 5	Вершина степени 4	Вершина степени 3
${ displaystyle 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} { текст {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} ~ ( times 1)}$	${ displaystyle 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 90 ^ { circ} { текст {-}} 90 ^ { circ} ~ ( times 2)}$	${ displaystyle 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 90 ^ { circ} { text {-}} 150 ^ { circ} ~ ( раз 2)}$	${ displaystyle 60 ^ { circ} { text {-}} 128 { frac {4} {7}} ^ { circ} { text {-}} 171 { frac {3} {7}} ^ { circ} ~ ( times 1)}$
	${ displaystyle 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 60 ^ { circ} { текст {-}} 120 ^ { circ} ~ ( times 1)}$	${ displaystyle 60 ^ { circ} { text {-}} 60 ^ { circ} { text {-}} 120 ^ { circ} { text {-}} 120 ^ { circ} ~ ( раз 2)}$	${ displaystyle 60 ^ { circ} { text {-}} 135 ^ { circ} { text {-}} 165 ^ { circ} ~ ( times 1)}$
		${ displaystyle 60 ^ { circ} { text {-}} 90 ^ { circ} { text {-}} 90 ^ { circ} { text {-}} 120 ^ { circ} ~ ( раз 2)}$	${ displaystyle 60 ^ { circ} { text {-}} 140 ^ { circ} { text {-}} 160 ^ { circ} ~ ( times 1)}$
		${ displaystyle 90 ^ { circ} { text {-}} 90 ^ { circ} { text {-}} 90 ^ { circ} { text {-}} 90 ^ { circ} ~ ( раз 1)}$	${ displaystyle 60 ^ { circ} { text {-}} 144 ^ { circ} { text {-}} 156 ~ ( times 1)}$
			${ displaystyle 60 ^ { circ} { text {-}} 150 ^ { circ} { text {-}} 150 ^ { circ} ~ ( times 1)}$
			${ displaystyle 90 ^ { circ} { text {-}} 108 ^ { circ} { text {-}} 162 ^ { circ} ~ ( times 1)}$
			${ displaystyle 90 ^ { circ} { text {-}} 120 ^ { circ} { text {-}} 150 ^ { circ} ~ ( times 1)}$
			${ displaystyle 90 ^ { circ} { text {-}} 135 ^ { circ} { text {-}} 135 ^ { circ} ~ ( times 1)}$ *
			${ displaystyle 108 ^ { circ} { text {-}} 108 ^ { circ} { text {-}} 144 ^ { circ} ~ ( times 1)}$
			${ displaystyle 120 ^ { circ} { text {-}} 120 ^ { circ} { text {-}} 120 ^ { circ} ~ ( times 1)}$

(треугольник с девичник дает 13.200-угольник, квадрат с семиугольник дает 9,3333-угольник, а пятиугольник с шестиугольником дает 7,5000-угольник). Тогда есть ${ Displaystyle 1 (1) + (1 (2) +1) + (3 (2) +1) + 10 = 21}$ комбинации правильных многоугольников, которые встречаются в вершине.

Только одиннадцать из них могут встречаться в однородной мозаике правильных многоугольников, как это было описано в предыдущих разделах. * The ${ displaystyle 90 ^ { circ} { text {-}} 135 ^ { circ} { text {-}} 135 ^ { circ} ~ ( times 1)}$ не может сосуществовать с вершинами других типов.

В частности, если три многоугольника пересекаются в вершине и у одного нечетное количество сторон, два других многоугольника должны быть одинаковыми. Если это не так, им пришлось бы чередовать первый многоугольник, что невозможно, если у него нечетное количество сторон. Из-за этого ограничения эти шесть не могут появляться ни в одной мозаике из правильных многоугольников:

3 полигона в вершине (нельзя использовать)
3.7.42	3.8.24	3.9.18	3.10.15	4.5.20	5².10

Эти четыре могут быть использованы в k-однородные мозаики:

4 полигона в вершине (можно смешивать с другими типами вершин)
Действительный вершины	3².4.12	3.4.3.12	3².6²	3.4².6
Пример 2-однородные мозаики	с 3⁶	с 3,12²	с (3.6)²	с (3.6)²
Действительный Полупланигоны	Двойной полупланигон: V3².4.12	Двойной полупланигон: V3.4.3.12	Двойной полупланигон: V3².6²	Двойной полупланигон: V3.4².6
Пример Двойная 2-форма Плитки (Двойные соединения)	с V3⁶	с V3.12²	с V (3.6)²	с V3.4².6

Наконец, все правильные многоугольники и используемые вершинные многоугольники представлены на втором изображении ниже, показывая их площади и длины сторон относительно ${ displaystyle s = 2 { sqrt {3}}}$ для любого правильного многоугольника.

Количество двойных однородных мозаик

Каждое двойственное равномерное замощение находится в соответствии 1: 1 с соответствующим равномерным замощением посредством построения указанных выше планигонов и наложения.

Такие периодические мозаики можно классифицировать по количеству орбиты вершин, ребер и плиток. Если есть k орбиты планигонов, мозаика известна как k-двойная форма или k-изоэдральная; если есть т орбиты двойственных вершин, как т-изогональный; если есть е орбиты ребер, как е-изотоксальный.

k-двойно-однородные мозаики с одинаковыми фигурами вершин можно идентифицировать по их группа обоев симметрия, которая идентична симметрии соответствующих k-однородная черепица.

1-двойственно-однородные мозаики включают 3 правильных мозаики и 8 мозаик Лавеса с 2 или более типами вершин правильной степени. Есть 20 2-двойственно-однородных мозаик, 61 3-дуально-однородные мозаики, 151 4-двойственно-однородные мозаики, 332 5-двойственно-однородных мозаики и 673 6-дуально-однородных мозаик. Каждый можно сгруппировать по номеру м различных вершинных фигур, которые также называются м-Архимедовы мозаики.^[7]

Наконец, если количество типов планигонов такое же, как однородность (м = k ниже), то замощение называется Krotenheerdt. В общем, равномерность больше или равна количеству типов вершин (м ≥ k), поскольку разные типы планигонов обязательно имеют разные орбиты, но не наоборот. Параметр м = п = k, таких двойственных мозаик для п = 1; 20 таких двойных мозаик для п = 2; 39 таких двойственных мозаик для п = 3; 33 таких двойных мозаики для п = 4; 15 таких двойных мозаик для п = 5; 10 таких двойственных мозаик для п = 6; и 7 таких двойственных мозаик для п = 7.

Регулярные плитки и мозаики Лавеса

Показаны 3 правильных и 8 полурегулярных мозаик Лавеса с правильными вершинными планигонами, окрашенными обратно пропорционально площади, как в конструкции.

Три регулярные планигоны (многоугольники) для масштабирования
	Треугольники	Квадраты	Шестиугольники
Плитка
Изображение
Конфиг	V6³	V4⁴	V3⁶

8 полуправильные планигоны масштабировать
	Треугольники
Плитка
Изображение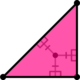
Конфиг	V4.8²	V3.12²	V4.6.12

	Четырехугольники
Плитка
Изображение
Конфиг	В (3,6)²	V3.4.6.4

	Пентагоны
Плитка
Изображение
Конфиг	V3⁴.6	V3².4.3.4	V3³.4²

Высшие двойные однородные мозаики

Вставки двойных планигонов в вершины более высоких степеней

Вершину шестой степени можно заменить центральным правильным шестиугольником и шестью исходящими из него ребрами;
Вершина двенадцатой степени может быть заменена шестью дельтоидами (центральным дельтовидным шестиугольником) и двенадцатью исходящими от него ребрами;
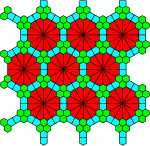
Вершину двенадцатой степени можно заменить шестью пятиугольниками Каира, центральным шестиугольником и двенадцатью исходящими от него ребрами (рассекая вершину шестой степени в центре предыдущего примера).

Двойные процессы (двойные «вставки»)

Дуалы Кротенхердта с двумя планигонами

Удалить при разрешении: Кроме того, я не вижу причин, по которым ваши изображения общий лучше, чем моя, что вы, кажется, предлагаете. Для этого нам может понадобиться третий читатель ... склонны ли читатели нет нажать на изображения, чтобы просмотреть их подробнее? Потому что в режиме проверки мои изображения более четкие, а в режиме чтения ваши изображения более четкие.

Есть 20 плиток, сделанных из 2 типов планигонов, двойных 2-однородные мозаики (Кротенхердт Duals):

Двойники 2-однородных мозаик (20)
п6м, * 632						p4m, * 442
[V3⁶; V3².4.3.4]	[V3.4.6.4; V3².4.3.4	[V3.4.6.4; V3³.4²]	[V3.4.6.4; V3.4².6]	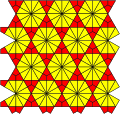[V4.6.12; V3.4.6.4]	[V3⁶; V3².4.12]	[3.12.12; 3.4.3.12]
п6м, * 632	п6, 632	п6, 632	см, 2 * 22	пмм, * 2222	см, 2 * 22	пмм, * 2222
[V3⁶; V3².6²]	[V3⁶; V3⁴.6]₁	[V3⁶; V3⁴.6]₂	[V3².6²; V3⁴.6]	[V3.6.3.6; V3².6²]	[V3.4².6; V3.6.3.6]]₂	[3.4².6; 3.6.3.6]₁
p4g, 4 * 2	пгг, 22 ×	см, 2 * 22	см, 2 * 22	пмм, * 2222	см, 2 * 22
[V3³.4²; V3².4.3.4]₁	[V3³.4²; V3².4.3.4]₂	[V4⁴; V3³.4²]₁	[V4⁴; V3³.4²]₂	[V3⁶; V3³.4²]₁	[V3⁶; V3³.4²]₂

Дуалы Кротенхердта с тремя планигонами

Плитка 3 вида плитки (39)
[V3.4²6; 3.6.3.6; V4.6.12] (v = 6, e = 7)	[V3⁶; 3²4,12; V4.6.12] (v = 5, e = 6)	[V3²4,12; 3.4.6.4; V3.12²] (v = 5, e = 6)	[V3.4.3.12; 3.4.6.4; 3,12²] (v = 5, e = 6)	[V3³4²; 3²4.12; 3.4.6.4] (v = 6, e = 8)
[V3⁶; V3³4²; V3²4.12] (v = 6, e = 7)	[V3⁶; V3²4.3.4; V3²4.12] (v = 5, e = 6)	[V3⁴6; V3³4²; V3²4.3.4] (v = 5, e = 6)	[V3⁶; V3²4.3.4; V3.4²6] (v = 5, e = 6)	[V3⁶; V3²4.3.4; V3.4.6.4] (v = 5, e = 6)
[V3⁶; V3³4²; V3.4.6.4] (v = 6, e = 6)	[V3⁶; V3²4.3.4; V3.4.6.4] (v = 6, e = 6)	[V3⁶; V3³4²; V3²4.3.4] (v = 4, e = 5)	[V3²4,12; V3.4.3.12; V3.12²] (v = 4, e = 7)	[V3.4.6.4; V3.4²6; V4⁴] (v = 3, e = 4)
[V3²4.3.4; V3.4.6.4; V3.4²6] (v = 4, e = 6)	[V3³4²; V3²4.3.4; 4⁴] (v = 4, e = 6)	[V3.4²6; V3.6.3.6; V4⁴] (v = 5, e = 7)	[V3.4²6; V3.6.3.6; V4⁴] (v = 6, e = 7)	[V3.4²6; V3.6.3.6; V4⁴] (v = 4, e = 5)
[V3.4²6; V3.6.3.6; V4⁴] (v = 5, e = 6)	[V3³4²; V3²6²; V3.4²6] (v = 5, e = 8)	[V3²6²; V3.4²6; 3.6.3.6] (v = 4, e = 7)	[V3²6²; V3.4²6; 3.6.3.6] (v = 5, e = 7)	[V3⁴6; V3³4²; V3.4²6] (v = 5, e = 7)
[V3²6²; V3.6.3.6; V6³] (v = 4, e = 5)	[V3²6²; V3.6.3.6; V6³] (v = 2, e = 4)	[V3⁴6; V3²6²; V6³] (v = 2, e = 5)	[V3⁶; V3²6²; V6³] (v = 2, e = 3)	[V3⁶; V3⁴6; V3²6²] (v = 5, e = 8)
[V3⁶; V3⁴6; V3²6²] (v = 3, e = 5)	[V3⁶; V3⁴6; V3²6²] (v = 3, e = 6)	[V3⁶; V3⁴6; V3.6.3.6] (v = 5, e = 6)	[V3⁶; V3⁴6; V3.6.3.6] (v = 4, e = 4)	[V3⁶; V3⁴6; V3.6.3.6] (v = 3, e = 3)
[V3⁶; V3³4²; V4⁴] (v = 4, e = 6)	[V3⁶; V3³4²; V4⁴] (v = 5, e = 7)	[V3⁶; V3³4²; V4⁴] (v = 3, e = 5)	[V3⁶; V3³4²; V4⁴] (v = 4, e = 6)

Дуалы Кротенхердта с четырьмя планигонами

4-однородные мозаики с 4 типами вершин (33)
[33434; 3²6²; 3446; 6³]	[3³4²; 3²6²; 3446; 46.12]	[33434; 3²6²; 3446; 46.12]	[3⁶; 3³4²; 33434; 334.12]	[3⁶; 33434; 334.12; 3.12²]
[3⁶; 33434; 343.12; 3.12²]	[3⁶; 3³4²; 33434; 3464]	[3⁶; 3³4²; 33434; 3464]	[3⁶; 33434; 3464; 3446]	[3⁴6; 3²6²; 3636; 6³]
[3⁴6; 3²6²; 3636; 6³]	[334.12; 343.12; 3464; 46.12]	[3³4²; 334.12; 343.12; 3.12²]	[3³4²; 334.12; 343.12; 4⁴]	[3³4²; 334.12; 343.12; 3.12²]
[3⁶; 3³4²; 33434; 4⁴]	[33434; 3²6²; 3464; 3446]	[3⁶; 3³4²; 3446; 3636]	[3⁶; 3⁴6; 3446; 3636]	[3⁶; 3⁴6; 3446; 3636]
[3⁶; 3⁴6; 3³4²; 3446]	[3⁶; 3⁴6; 3³4²; 3446]	[3⁶; 3⁴6; 3²6²; 6³]	[3⁶; 3⁴6; 3²6²; 6³]	[3⁶; 3⁴6; 3²6²; 6³]
[3⁶; 3⁴6; 3²6²; 6³]	[3⁶; 3⁴6; 3²6²; 3636]	[3³4²; 3²6²; 3446; 6³]	[3³4²; 3²6²; 3446; 6³]	[3²6²; 3446; 3636; 4⁴]
*33 Krotenheerdt-4 Двойной*	[3²6²; 3446; 3636; 4⁴]	[3²6²; 3446; 3636; 4⁴]	[3²6²; 3446; 3636; 4⁴]	*33 Krotenheerdt-4 Двойной*

Дуалы Кротенхердта с пятью планигонами

Есть 15 5-однородные двойственные мозаики с 5 уникальными планигонами.

5-однородные двойные мозаики, 5 планжонов
V [33434; 3²6²; 3464; 3446; 6³]	V [3⁶; 3⁴6; 3²6²; 3636; 6³]	V [3⁶; 3⁴6; 3³4²; 3446; 46.12]	V [3⁴6; 3³4²; 33434; 3446; 4⁴]	V [3⁶; 33434; 3464; 3446; 3636]
V [3⁶; 3⁴6; 3464; 3446; 3636]	V [33434; 334,12; 3464; 3.12.12; 46.12]	V [3⁶; 3⁴6; 3446; 3636; 4⁴]	V [3⁶; 3⁴6; 3446; 3636; 4⁴]	V [3⁶; 3⁴6; 3446; 3636; 4⁴]
V [3⁶; 3⁴6; 3446; 3636; 4⁴]	V [3⁶; 3³4²; 3446; 3636; 4⁴]	V [3⁶; 3⁴6; 3³4²; 3446; 4⁴]	V [3⁶; 3³4²; 3²6²; 3446; 3636]	[3⁶; 3⁴6; 3³4²; 3²6²; 3446]

Дуалы Кротенхердта с шестью планигонами

Есть 10 6-однородные двойственные мозаики с 6 уникальными планигонами.

6-однородные двойственные мозаики, 6 планигонов
[V4⁴; V3.4.6.4; V3.4.4.6; ².4.3.4; V3³.4²; V3².6²]	; V3⁴.6; V3.4.4.6; V3².4.3.4; V3³.4²; V3².6²]	[V4⁴; V3⁴.6; V3.4.4.6; V3⁶; V3³.4²; V3².6²]	[V4⁴; V3.4.6.4; V3.4.4.6; В (3,6)²; V3³.4²; V3².46; V3⁶; V3³.4²; V3².4.3.4]
[V3⁶, V3.4.6.4; V3.4.4.6; V3².4.3.4; V3³.4²; V3².6²]	[V3⁴.6; V3.4.6.4; V3.4.4.6; V3².6²; V3³.4²; V3².4.3.4]	[V3⁶; V3.4.6.4; V3.4.4.6; В (3,6)²; V3³.4²; V3².4.12]	[V3⁶; V3.4.6.4; V3.4.4.6; V3⁴.6; V3³.4²; V3².4.3.4]	[V3⁴.6; V3.4.6.4; V3.4.4.6; В (3,6)²; V3³.4²; V3².4.3.4]

Дуалы Кротенхердта с семью планигонами

Есть 7 7-однородные двойственные мозаики с 7 уникальными планигонами.

7-однородные двойственные мозаики, 7 планигонов
V [3⁶; 3³.4²; 3².4.3.4; 4⁴; 3.4².6; 3².6²; 6³]	V [3⁶; 3³.4²; 3².4.3.4; 3⁴.6; 3.4².6; 3².4.12; 4.6.12]	V [3³.4²; 3².4.3.4; 3.4².6; 3².6²; 3².4.12; 4.6.12]	V [3⁶; 3².4.3.4; 4⁴; 3.4².6; 3⁴.6; 3.4.6.4; (3.6)²]
V [3⁶; 3³.4²; 3².4.3.4; 3⁴.6; 3.4².6; 3.4.6.4; (3.6)²]₁	V [3⁶; 3³.4²; 3².4.3.4; 3⁴.6; 3.4².6; 3.4.6.4; 3².4.12]	V [3⁶; 3³.4²; 3².4.3.4; 3⁴.6; 3.4².6; 3.4.6.4; (3.6)²]₂	V [3⁶; 3³.4²; 3².4.3.4; 3⁴.6; 3.4².6; 3².4.12; 4.6.12]

Как ни странно, 5-й и 7-й двойственные мозаики Кротенхердта uniform-7 имеют одинаковые типы вершин, хотя и не похожи друг на друга!

Из ${ displaystyle n geq 8}$ вперед, униформы нет п мозаики с п типы вершин или без униформы п двойные с п отчетливые (полу) планигоны.^[8]

Фрактализация Dual k-Равномерная мозаика

Есть много способов генерировать новые k-двойственно-однородные мозаики из старых k-однородных мозаик. Например, обратите внимание, что 2-форма V [3.12.12; 3.4.3.12] мозаика имеет квадратную решетку, 4 (3-1) -однородную V [343.12; (3,12²)³] тайлинг имеет плоскую квадратную решетку и 5 (3-1-1) -однородную V [334.12; 343,12; (3.12.12) 3] тайлинг имеет вытянутую треугольную решетку. Эти равномерные мозаики более высокого порядка используют ту же решетку, но обладают большей сложностью. Двойная фрактальная основа этих мозаик такова:

	Треугольник	Квадрат	Шестиугольник	Рассеченный Додекагон
Форма
Фрактализация (Двойной)

Длина сторон увеличена в раз ${ displaystyle 2 + { sqrt {3}}}$ :

Каждый треугольник заменяется тремя V [3.12²] многоугольники (единица 1-двойственно-однородной V [3.12²] черепица);
Каждый квадрат заменяется четырьмя V [3.12²] и четырех многоугольников V [3.4.3.12] (единица 2-двойственно-однородной V [3.12²; V3.4.3.12] тайлинг);
Каждый шестиугольник заменен шестью дельтоидами V [3.4.6.4], шестью связками V [3.4.3.12] и шестью V [3.12²] многоугольники (единица этой 3-двойственно-однородной мозаики)
Каждый двенадцатигранник разделен на шесть больших треугольников, шесть больших квадратов и один центральный шестиугольник, все из которых состоят из вышеперечисленных.

Это можно сделать аналогично с усеченным трехгексагональным замощением в качестве основы с соответствующим растяжением ${ displaystyle 3 + { sqrt {3}}}$ .

	Треугольник	Квадрат	Шестиугольник	Рассеченный Додекагон
Форма
Фрактализация (Двойной)

Каждый треугольник заменяется тремя многоугольниками V [4.6.12] (единица 1-двойственно-однородного V [4.6.12] разбиения);
Каждый квадрат заменяется одним квадратом, четырьмя V [3³.4²] многоугольников, четырех V [3.4.3.12] многоугольников и четырех V [3².4.12] многоугольники (единица этого 4-двойственно-однородного разбиения Кротенхердта);
Каждый шестиугольник заменен шестью дельтоидами V [3.4.6.4] и тридцатью шестью многоугольниками V [4.6.12] (единица этого 5-двойственно-однородного мозаичного покрытия).
Каждый двенадцатигранник разделен на шесть больших треугольников, шесть больших квадратов и один центральный шестиугольник, все из которых состоят из вышеперечисленных.

Примеры фрактализации

	Усеченная шестиугольная мозаика	Усеченная трехгексагональная мозаика
Двойной Фрактализация

Разное

Сравнение 65 k однородных мозаик в однородных плоских мозаиках и их двойственных однородных мозаиках. Два нижних ряда совпадают и масштабируются.

Сравнение 65 k равномерные мозаики в равномерные плоские мозаики и их двойственные однородные мозаики. Два нижних ряда совпадают и масштабируются.

Navigation