WikiDer > Обозначения многогранника Конвея

Conway polyhedron notation

Этот пример диаграммы показывает, как 11 новых форм могут быть получены из куба с помощью 3 операций. Новые многогранники показаны в виде карт на поверхности куба, поэтому топологические изменения более очевидны. Вершины всех форм отмечены кружками.

В геометрии Обозначения многогранника Конвея, изобретенный Джон Хортон Конвей и продвигается Джордж У. Харт, используется для описания многогранники на основе семенного многогранника, модифицированного различными приставками операции.^[1]^[2]

Конвей и Харт расширили идею использования операторов, таких как усечение как определено Кеплер, чтобы построить связанные многогранники одинаковой симметрии. Например, tC представляет усеченный куб, и ТАС, разбирается как ${displaystyle t (aC)}$ , является (топологически) а усеченный кубооктаэдр. Самый простой оператор двойной меняет местами вершины и грани; например, дуальный куб - это октаэдр: Округ Колумбия=О. Примененные последовательно, эти операторы позволяют генерировать много многогранников более высокого порядка. Конвей определил операторов abdegjkmost, а Харт добавил р и п.^[3] Более поздние реализации называли дополнительные операторы, иногда называемые «расширенными» операторами.^[4]^[5] Базовых операций Конвея достаточно для создания Архимедов и Каталонские твердые вещества из Платоновых тел. Некоторые базовые операции могут быть составными из других: например, двойное применение амвона - это операция расширения: аа = е, а усечение после амвона дает скос: та = б.

Многогранники могут быть изучены топологически с точки зрения того, как их вершины, ребра и грани соединяются вместе, или геометрически, с точки зрения размещения этих элементов в пространстве. Различные реализации этих операторов могут создавать геометрически разные, но топологически эквивалентные многогранники. Эти топологически эквивалентные многогранники можно рассматривать как один из многих вложения из многогранный граф на сфере. Если не указано иное, в этой статье (и в литературе по операторам Конвея в целом) первоочередное внимание уделяется топологии. Многогранники с род 0 (т.е. топологически эквивалентен сфере) часто помещаются в каноническая форма чтобы избежать двусмысленности.

Операторы

В обозначениях Конвея операции с многогранниками применяются как функции, справа налево. Например, кубооктаэдр является амвонский куб,^[6] т.е. ${displaystyle a (C) = aC}$ , а усеченный кубооктаэдр является ${displaystyle t (a (C)) = t (aC) = taC}$ . Повторное применение оператора можно обозначить показателем степени: j² = о. В общем, операторы Конвея не коммутативный.

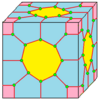
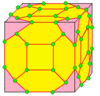
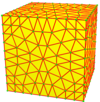
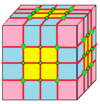
Можно визуализировать отдельных операторов в виде фундаментальные области (или камеры), как показано ниже. Каждый прямоугольный треугольник - это фундаментальная область. Каждая белая камера представляет собой повернутую версию других, как и каждая цветная камера. За ахиральный операторов, цветные камеры являются отражением белых камер, и все они транзитивны. В групповом плане ахиральные операторы соответствуют диэдральные группы $D п$ куда п - количество сторон грани, а киральные операторы соответствуют циклические группы $C п$ лишены отражательной симметрии диэдральных групп. Ахирал и хиральный Операторы также называются локальными операциями, сохраняющими симметрию (LSP) и локальными операциями, сохраняющими симметрию, сохраняющими ориентацию (LOPSP), соответственно.^[7]^[8]^[9]LSP следует понимать как локальные операции, сохраняющие симметрию, а не как операции, сохраняющие локальную симметрию. Опять же, это симметрии в топологическом, а не геометрическом смысле: точные углы и длины ребер могут отличаться.

Фундаментальные области лиц с ${displaystyle n}$ стороны
3 (треугольник)	4 (квадрат)	5 (Пентагон)	6 (шестиугольник)

Фундаментальные области для групп полиэдров. Группы ${displaystyle D_ {3}, D_ {4}, D_ {5}, D_ {6}}$ для ахиральных многогранников и ${displaystyle C_ {3}, C_ {4}, C_ {5}, C_ {6}}$ для киральных многогранников.

Харт представил оператор отражения р, что дает зеркальное отображение многогранника.^[6] Это не совсем LOPSP, поскольку он не сохраняет ориентацию: он меняет ее местами, меняя местами белые и красные камеры. р не влияет на ахиральные многогранники, кроме ориентации, и rr = S возвращает исходный многогранник. Верхняя черта может использоваться для обозначения другой хиральной формы оператора: s = RSR.

Операция неприводима, если она не может быть выражена как композиция операторов, кроме d и р. Большинство исходных операторов Конвея неприводимы: исключения е, б, о, и м.

Матричное представление

Икс	${displaystyle {egin {bmatrix} a & b & c 0 & d & 0 a '& b' & c'end {bmatrix}} = mathbf {M} _ {x}}$
xd	${displaystyle {egin {bmatrix} c & b & a 0 & d & 0 c '& b' & a'end {bmatrix}} = mathbf {M} _ {x} mathbf {M} _ {d}}$
dx	${displaystyle {egin {bmatrix} a '& b' & c ' 0 & d & 0 a & b & cend {bmatrix}} = mathbf {M} _ {d} mathbf {M} _ {x}}$
dxd	${displaystyle {egin {bmatrix} c '& b' & a ' 0 & d & 0 c & b & aend {bmatrix}} = mathbf {M} _ {d} mathbf {M} _ {x} mathbf {M} _ {d}}$

Связь между количеством вершин, ребер и граней семени и многогранника, созданного операциями, перечисленными в этой статье, может быть выражена в виде матрицы ${displaystyle mathbf {M} _ {x}}$ . Когда Икс это оператор, ${displaystyle v, e, f}$ - вершины, ребра и грани семени (соответственно), а ${displaystyle v ', e', f '}$ - вершины, ребра и грани результата, тогда

{displaystyle mathbf {M} _ {x} {egin {bmatrix} v e fend {bmatrix}} = {egin {bmatrix} v ' e' f'end {bmatrix}}}

.

Матрица для композиции двух операторов - это просто произведение матриц для двух операторов. Различные операторы могут иметь одинаковую матрицу, например, п и л. Количество краев результата является целым кратным d начального уровня: это называется темпом инфляции или краевым фактором.^[7]

Простейшие операторы оператор идентификации S и двойной оператор d, имеют простые матричные формы:

{displaystyle mathbf {M} _ {S} = {egin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1end {bmatrix}} = mathbf {I} _ {3}}

,

{displaystyle mathbf {M} _ {d} = {egin {bmatrix} 0 & 0 & 1 0 & 1 & 0 1 & 0 & 0end {bmatrix}}}

Два двойных оператора сокращаются; дд = S, а квадрат ${displaystyle mathbf {M} _ {d}}$ это единичная матрица. Применительно к другим операторам дуальный оператор соответствует горизонтальному и вертикальному отражениям матрицы. Операторы могут быть сгруппированы в группы по четыре (или меньше, если некоторые формы одинаковы) путем идентификации операторов. Икс, xd (оператор двойственного), dx (двойственный к оператору), и dxd (сопряжение оператора). В этой статье только матрица для Икс дается, так как остальные являются простыми отражениями.

Количество операторов

Количество LSP для каждого уровня инфляции составляет ${displaystyle 2,2,4,6,6,20,28,58,82, cdots}$ начиная с уровня инфляции 1. Однако не все LSP обязательно образуют многогранник, ребра и вершины которого образуют 3-связный граф, и как следствие Теорема Стейница не обязательно производить выпуклый многогранник из выпуклого семени. Количество 3-связанных LSP для каждого уровня инфляции составляет ${displaystyle 2,2,4,6,4,20,20,54,64, cdots}$ .^[8]

Исходные операции

Строго говоря, семя (S), иголка (п) и zip (z) не были включены Конвеем, но они связаны с оригинальными операциями Конвея по дуальности, поэтому включены здесь.

С этого момента операции визуализируются с семенами куба, нарисованными на поверхности этого куба. Синие грани пересекают края семени, а розовые грани лежат над вершинами семени. Существует некоторая гибкость в точном размещении вершин, особенно с киральными операторами.

Оригинальные операторы Конвея
Краевой фактор	Матрица ${displaystyle mathbf {M} _ {x}}$	Икс	xd	dx	dxd	Примечания
1	${displaystyle {egin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1end {bmatrix}}}$	Семя: S	Двойной: d		Семя: дд = S	Dual заменяет каждую грань вершиной, а каждую вершину - гранью.
2	${displaystyle {egin {bmatrix} 1 & 0 & 1 0 & 2 & 0 0 & 1 & 0end {bmatrix}}}$	Присоединиться: j		Амбо: а		Соединение создает четырехугольные грани. Амбо создает вершины четвертой степени и также называется исправление, или медиальный график в теории графов.^[10]
3	${displaystyle {egin {bmatrix} 1 & 0 & 1 0 & 3 & 0 0 & 2 & 0end {bmatrix}}}$	Кис: k	Иголка: п	Почтовый индекс: z	Усечь: т	Кис поднимает пирамиду на каждом лице, что также называется акисатион, Kleetope, кумуляция,^[11] аккреция, или пирамида-увеличение. Усечь отрезает многогранник в его вершинах, но оставляет часть исходных ребер.^[12] Zip также называют битовое усечение.
4	${displaystyle {egin {bmatrix} 1 & 1 & 1 0 & 4 & 0 0 & 2 & 0end {bmatrix}}}$	Орто: о = jj		Расширять: е = аа
5	${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 5 & 0 0 & 2 & 0end {bmatrix}}}$	Гироскоп: грамм	б-г = rgr	SD = RSR	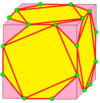Курносый: s	Киральные операторы. Видеть Курносый (геометрия). В отличие от Харта,^[3] б-г не то же самое, что грамм: это его киральная пара.^[13]
6	${displaystyle {egin {bmatrix} 1 & 1 & 1 0 & 6 & 0 0 & 4 & 0end {bmatrix}}}$	Мета: м = кДж		Скос: б = та

Семена

Любой многогранник может служить семенем, если над ним можно выполнять операции. Обычным семенам присвоена буква. Платоновы тела представлены первой буквой их имени (Тэтраэдр, Окаэдр, Cубе, якосаэдр, Dодекаэдр); то приски (п_п) за п-гональные формы; антипризмы (А_п); cтыPolae (U_п); anticupolae (V_п); и пурамиды (Y_п). Любой JOhnson Solid может называться J_п, за п=1..92.

Все пять правильных многогранников можно сгенерировать из призматических образующих от нуля до двух операторов:^[14]

Треугольная пирамида: Y₃ (Тетраэдр - это особая пирамида)
- Т = Y₃
- О = в (амвонский тетраэдр)
- C = jT (соединить тетраэдр)
- я = СТ (курносый тетраэдр)
- D = gT (гиротетраэдр)
Треугольная антипризма: А₃ (Октаэдр - особая антипризма)
- О = А₃
- C = dA₃
Квадратная призма: п₄ (Куб - это особая призма)
- C = п₄
Пятиугольная антипризма: А₅
- я = k₅А₅ (Специальный гиродлинная дипирамида)
- D = т₅dA₅ (Специальный усеченный трапецоэдр)

Обычные евклидовы мозаики также можно использовать как семена:

Q = Кадриль = Квадратная плитка
H = Hextille = Шестиугольная черепица = d 螖
螖 = Дельтиль = Треугольная черепица = dH

Расширенные операции

Это операции, созданные по оригинальному набору Конвея. Обратите внимание, что существует гораздо больше операций, чем было названо; просто потому, что здесь нет операции, не означает, что она не существует (или не является LSP или LOPSP). Для упрощения в этот список включены только неприводимые операторы: другие могут быть созданы путем объединения операторов вместе.

Неприводимые расширенные операторы
Краевой фактор	Матрица ${displaystyle mathbf {M} _ {x}}$	Икс	xd	dx	dxd	Примечания
4	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 4 & 0 0 & 1 & 1end {bmatrix}}}$	Фаска: c	CD = ду	Округ Колумбия = уд	Подразделить: ты	Фаска - это форма соединения л. Видеть Фаска (геометрия).
5	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 5 & 0 0 & 2 & 1end {bmatrix}}}$	Пропеллер: п	дп = pd		dpd = п	Киральные операторы. Оператор пропеллера был разработан Джорджем Хартом.^[15]
5	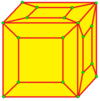${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 5 & 0 0 & 2 & 1end {bmatrix}}}$	Лофт: л	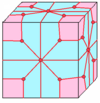ld	дл	dld
6	${displaystyle {egin {bmatrix} 1 & 3 & 0 0 & 6 & 0 0 & 2 & 1end {bmatrix}}}$	Quinto: q	qd	dq	dqd
6	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 6 & 0 0 & 3 & 1end {bmatrix}}}$	Соединить кружево: L₀	L₀d	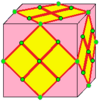дл₀	дл₀d	См. Ниже объяснение нотации соединения.
7	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 7 & 0 0 & 4 & 1end {bmatrix}}}$	Кружево: L	Ld	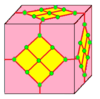дл	dLd
7	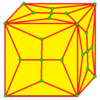${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 7 & 0 0 & 4 & 0end {bmatrix}}}$	Ставка: K	Kd	dK	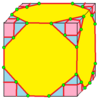dKd
7	${displaystyle {egin {bmatrix} 1 & 4 & 0 0 & 7 & 0 0 & 2 & 1end {bmatrix}}}$	Вихрь: ш	wd = dv	vd = dw	Улитка: v	Киральные операторы.
8	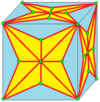${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 8 & 0 0 & 5 & 0end {bmatrix}}}$	Присоединяйтесь-кис-кис: ${displaystyle (kk) _ {0}}$	${displaystyle (kk) _ {0} d}$	${displaystyle d (kk) _ {0}}$	${displaystyle d (kk) _ {0} d}$	Иногда называют J.^[4] См. Ниже объяснение нотации соединения. Несоединяемая форма, кк, не является неприводимым.
10	${displaystyle {egin {bmatrix} 1 & 3 & 1 0 & 10 & 0 0 & 6 & 0end {bmatrix}}}$	Крест: Икс	Xd	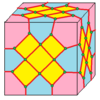dX	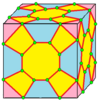dXd

Индексированные расширенные операции

Ряд операторов можно сгруппировать по некоторым критериям или изменить их поведение с помощью индекса.^[4] Они записываются как оператор с нижним индексом: Икс_п.

Увеличение

Увеличение операции сохраняют исходные края. Они могут применяться к любому независимому подмножеству лиц или могут быть преобразованы в присоединиться-формовать, удалив исходные края. Обозначение Конвея поддерживает необязательный индекс для этих операторов: 0 для формы соединения или 3 или выше для количества сторон затронутых граней. Например, k₄Y₄= O: если взять пирамиду с квадратным основанием и приклеить другую пирамиду к квадратному основанию, получится октаэдр.

Оператор	k	л	L	K	(кк)
Икс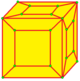
Икс₀	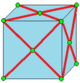k₀ = j	л₀ = c	L₀	K₀ = jk	${displaystyle (kk) _ {0}}$
Увеличение	Пирамида	Призма	Антипризма

Оператор усечения т также имеет форму индекса т_п, что указывает на то, что усекаются только вершины определенной степени. Это эквивалентно dk_пd.

Некоторые из расширенных операторов могут быть созданы в особых случаях с помощью k_п и т_п операторы. Например, куб с фаской, cC, можно построить как т₄daC, как ромбический додекаэдр, daC или же jC, с усеченными вершинами степени 4. Поднятый куб, lC такой же как т₄kC. Квинтододекаэдр, qD можно построить как т₅даад или же т₅deD или же т₅oD, а дельтовидный гексеконтаэдр, deD или же oD, с усеченными вершинами степени 5.

Мета / скос

Meta добавляет вершины в центре и по краям, а Bevel добавляет грани в центре, исходные вершины и по краям. Индекс показывает, сколько вершин или граней добавлено по краям. Мета (в неиндексированной форме) также называется усечение или же омниусечение. Обратите внимание, что 0 здесь не означает то же самое, что и для операций увеличения: это означает, что по краям добавляются нулевые вершины (или грани).^[4]

Операторы Meta / Bevel
п	Краевой фактор	Матрица ${displaystyle mathbf {M} _ {x}}$	Икс	xd	dx	dxd
0	3	${displaystyle {egin {bmatrix} 1 & 0 & 1 0 & 3 & 0 0 & 2 & 0end {bmatrix}}}$	k = м₀	п	z = б₀	т
1	6	${displaystyle {egin {bmatrix} 1 & 1 & 1 0 & 6 & 0 0 & 4 & 0end {bmatrix}}}$	м = м₁ = кДж		б = б₁ = та
2	9	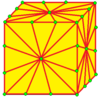${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 9 & 0 0 & 6 & 0end {bmatrix}}}$	м₂	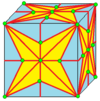м₂d	б₂	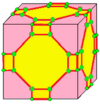б₂d
3	12	${displaystyle {egin {bmatrix} 1 & 3 & 1 0 & 12 & 0 0 & 8 & 0end {bmatrix}}}$	м₃	м₃d	б₃	б₃d
п	3п+3	${displaystyle {egin {bmatrix} 1 & n & 1 0 & 3n + 3 & 0 0 & 2n + 2 & 0end {bmatrix}}}$	м_п	м_пd	б_п	б_пd

Медиальный

Медиал похож на мета, за исключением того, что он не добавляет ребер от центра к каждой исходной вершине. Форма индекса 1 идентична операторам орто и расширения Конвея: расширение также называется песня и расширение. Обратите внимание, что о и е имеют свои собственные индексированные формы, описанные ниже. Также обратите внимание, что некоторые реализации начинают индексацию с 0 вместо 1.^[4]

Медиальные операторы
п	Край фактор	Матрица ${displaystyle mathbf {M} _ {x}}$	Икс	xd	dx	dxd
1	4	${displaystyle {egin {bmatrix} 1 & 1 & 1 0 & 4 & 0 0 & 2 & 0end {bmatrix}}}$	M₁ = о = jj		е = аа
2	7	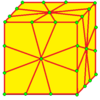${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 7 & 0 0 & 4 & 0end {bmatrix}}}$	Медиальный: M = M₂	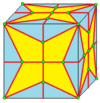Мкр	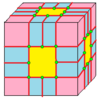дМ	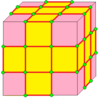dMd
п	3п+1	${displaystyle {egin {bmatrix} 1 & n & 1 0 & 3n + 1 & 0 0 & 2n & 0end {bmatrix}}}$	M_п	M_пd	дМ_п	дМ_пd

Гольдберг-Кокстер

Операторы Гольдберга-Кокстера (ГК) Конвея - это два бесконечных семейства операторов, которые являются расширением Построение Гольдберга-Кокстера.^[16]^[17] Конструкцию GC можно представить как взятие треугольной части треугольной решетки или квадратной части квадратной решетки и наложение ее на каждую грань многогранника. Эту конструкцию можно распространить на любую грань, определив камеры треугольника или квадрата («главный многоугольник»).^[7] Операторы из семейства треугольников могут использоваться для создания Многогранники Гольдберга и геодезические многогранники: видеть Список геодезических многогранников и многогранников Гольдберга для формул.

Эти два семейства представляют собой треугольное семейство GC, c_{а, б} и ты_{а, б}, и семейство четырехугольника GC, е_{а, б} и о_{а, б}. Оба семейства GC индексируются двумя целыми числами ${displaystyle ageq 1}$ и ${displaystyle bgeq 0}$ . Они обладают множеством приятных качеств:

Индексы семей связаны с определенными Евклидовы области над комплексными числами: Целые числа Эйзенштейна для семейства треугольных GC, а Гауссовские целые числа для четырехугольника семейства GC.
Операторы в Икс и dxd столбцы внутри одной семьи перемещаются друг с другом.

Операторы разделены на три класса (примеры написаны в терминах c но применимо ко всем 4 операторам):

Класс I: ${displaystyle b = 0}$ . Ахиральный, сохраняет оригинальные края. Может быть записано с подавленным нулевым индексом, например c_а,0 = c_а.
Класс II: ${displaystyle a = b}$ . Тоже ахирал. Можно разложить как c_{а, а} = c_аc_1,1
Класс III: все остальные операторы. Это хиральные и c_{а, б} и c_{б, а} являются киральными парами друг друга.

Из оригинальных операций Конвея единственными, которые не попадают в семейство GC, являются грамм и s (гироскоп и курносый). Мета и скос (м и б) можно выразить через один оператор из треугольного семейства и один из четырехугольного семейства.

Треугольная

Треугольные операторы Гольдберга-Кокстера.
а	б	Учебный класс	Краевой фактор Т = а² + ab + b²	Матрица ${displaystyle mathbf {M} _ {x}}$	Главный треугольник	Икс	xd	dx	dxd
1	0	я	1	${displaystyle {egin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1end {bmatrix}}}$		ты₁ = S	d		c₁ = S
2	0	я	4	${displaystyle {egin {bmatrix} 1 & 1 & 0 0 & 4 & 0 0 & 2 & 1end {bmatrix}}}$		ты₂ = ты	Округ Колумбия	ду	c₂ = c
3	0	я	9	${displaystyle {egin {bmatrix} 1 & 2 & 1 0 & 9 & 0 0 & 6 & 0end {bmatrix}}}$		ты₃ = nn	нк	zt	c₃ = zz
4	0	я	16	${displaystyle {egin {bmatrix} 1 & 5 & 0 0 & 16 & 0 0 & 10 & 1end {bmatrix}}}$		ты₄ = уу	уд = dcc	дуу = ccd	c₄ = cc
5	0	я	25	${displaystyle {egin {bmatrix} 1 & 8 & 0 0 & 25 & 0 0 & 16 & 1end {bmatrix}}}$		ты₅	ты₅d = Округ Колумбия₅	ду₅ = c₅d	c₅
6	0	я	36	${displaystyle {egin {bmatrix} 1 & 11 & 1 0 & 36 & 0 0 & 24 & 0end {bmatrix}}}$		ты₆ = unn	unk	czt	ты₆ = czz
7	0	я	49	${displaystyle {egin {bmatrix} 1 & 16 & 0 0 & 49 & 0 0 & 32 & 1end {bmatrix}}}$		ты₇ = ты_2,1ты_1,2 = VRV	vrvd = dwrw	dvrv = wrwd	c₇ = c_2,1c_1,2 = wrw
8	0	я	64	${displaystyle {egin {bmatrix} 1 & 21 & 0 0 & 64 & 0 0 & 42 & 1end {bmatrix}}}$		ты₈ = ты³	ты³d = Округ Колумбия³	ду³ = c³d	c₈ = c³
9	0	я	81	${displaystyle {egin {bmatrix} 1 & 26 & 1 0 & 81 & 0 0 & 54 & 0end {bmatrix}}}$		ты₉ = п⁴	п³k = kz³	tn³ = z³т	c₉ = z⁴
1	1	II	3	${displaystyle {egin {bmatrix} 1 & 0 & 1 0 & 3 & 0 0 & 2 & 0end {bmatrix}}}$		ты_1,1 = п	k	т	c_1,1 = z
2	1	III	7	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 7 & 0 0 & 4 & 1end {bmatrix}}}$		v = ты_2,1	vd = dw	dv = wd	ш = c_2,1
3	1	III	13	${displaystyle {egin {bmatrix} 1 & 4 & 0 0 & 13 & 0 0 & 8 & 1end {bmatrix}}}$		ты_3,1	ты_3,1d = Округ Колумбия_3,1	ду_3,1 = c_3,1d	c_3,1
3	2	III	19	${displaystyle {egin {bmatrix} 1 & 6 & 0 0 & 19 & 0 0 & 12 & 1end {bmatrix}}}$		ты_3,2	ты_3,2d = Округ Колумбия_3,2	ду_3,2 = c_3,2d	c_3,2
4	3	III	37	${displaystyle {egin {bmatrix} 1 & 12 & 0 0 & 37 & 0 0 & 24 & 1end {bmatrix}}}$		ты_4,3	ты_4,3d = Округ Колумбия_4,3	ду_4,3 = c_4,3d	c_4,3
5	4	III	61	${displaystyle {egin {bmatrix} 1 & 20 & 0 0 & 61 & 0 0 & 40 & 1end {bmatrix}}}$		ты_5,4	ты_5,4d = Округ Колумбия_5,4	ду_5,4 = c_5,4d	c_5,4
6	5	III	91	${displaystyle {egin {bmatrix} 1 & 30 & 0 0 & 91 & 0 0 & 60 & 1end {bmatrix}}}$		ты_6,5 = ты_1,2ты_1,3	ты_6,5d = Округ Колумбия_6,5	ду_6,5 = c_6,5d	c_6,5=c_1,2c_1,3
7	6	III	127	${displaystyle {egin {bmatrix} 1 & 42 & 0 0 & 127 & 0 0 & 84 & 1end {bmatrix}}}$		ты_7,6	ты_7,6d = Округ Колумбия_7,6	ду_7,6 = c_7,6d	c_7,6
8	7	III	169	${displaystyle {egin {bmatrix} 1 & 56 & 0 0 & 169 & 0 0 & 112 & 1end {bmatrix}}}$		ты_8,7 = ты_3,1²	ты_8,7d = Округ Колумбия_8,7	ду_8,7 = c_8,7d	c_8,7 = c_3,1²
9	8	III	217	${displaystyle {egin {bmatrix} 1 & 72 & 0 0 & 217 & 0 0 & 144 & 1end {bmatrix}}}$		ты_9,8 = ты_2,1ты_5,1	ты_9,8d = Округ Колумбия_9,8	ду_9,8 = c_9,8d	c_9,8 = c_2,1c_5,1
${displaystyle aequiv b}$ ${displaystyle (mathrm {mod} 3)}$		I, II или III	${displaystyle Tequiv 0}$ ${displaystyle (mathrm {mod} 3)}$	${displaystyle {egin {bmatrix} 1 & {frac {T} {3}} - 1 & 1 0 & T & 0 0 & {frac {2} {3}} T & 0end {bmatrix}}}$	...	ты_{а, б}	ты_{а, б}d = Округ Колумбия_{а, б}	ду_{а, б} = c_{а, б}d	c_{а, б}
${displaystyle aot Equiv b}$ ${displaystyle (mathrm {mod} 3)}$		I или III	${displaystyle Tequiv 1}$ ${displaystyle (mathrm {mod} 3)}$	${displaystyle {egin {bmatrix} 1 & {frac {T-1} {3}} & 0 0 & T & 0 0 & 2 {frac {T-1} {3}} & 1end {bmatrix}}}$	...	ты_{а, б}	ты_{а, б}d = Округ Колумбия_{а, б}	ду_{а, б} = c_{а, б}d	c_{а, б}

Согласно основной теории чисел, для любых значений а и б, ${displaystyle Tot Equiv 2 (mathrm {mod} 3)}$ .

Четырехугольник

Четырехугольные операторы Гольдберга-Кокстера
а	б	Учебный класс	Краевой фактор Т = а² + b²	Матрица ${displaystyle mathbf {M} _ {x}}$	Мастер-квадрат	Икс	xd	dx	dxd
1	0	я	1	${displaystyle {egin {bmatrix} 1 & 0 & 0 0 & 1 & 0 0 & 0 & 1end {bmatrix}}}$		о₁ = S	е₁ = d		о₁ = дд = S
2	0	я	4	${displaystyle {egin {bmatrix} 1 & 1 & 1 0 & 4 & 0 0 & 2 & 0end {bmatrix}}}$		о₂ = о = j²		е₂ = е = а²
3	0	я	9	${displaystyle {egin {bmatrix} 1 & 4 & 0 0 & 9 & 0 0 & 4 & 1end {bmatrix}}}$		о₃	е₃		о₃
4	0	я	16	${displaystyle {egin {bmatrix} 1 & 7 & 1 0 & 16 & 0 0 & 8 & 0end {bmatrix}}}$		о₄ = оо = j⁴		е₄ = ее = а⁴
5	0	я	25	${displaystyle {egin {bmatrix} 1 & 12 & 0 0 & 25 & 0 0 & 12 & 1end {bmatrix}}}$		о₅ = о_2,1о_1,2 = прп	е₅ = е_2,1е_1,2		о₅= dprpd
6	0	я	36	${displaystyle {egin {bmatrix} 1 & 17 & 1 0 & 36 & 0 0 & 18 & 0end {bmatrix}}}$		о₆ = о₂о₃		е₆ = е₂е₃
7	0	я	49	${displaystyle {egin {bmatrix} 1 & 24 & 0 0 & 49 & 0 0 & 24 & 1end {bmatrix}}}$		о₇	е₇		о₇
8	0	я	64	${displaystyle {egin {bmatrix} 1 & 31 & 1 0 & 64 & 0 0 & 32 & 0end {bmatrix}}}$		о₈ = о³ = j⁶		е₈ = е³ = а⁶
9	0	я	81	${displaystyle {egin {bmatrix} 1 & 40 & 0 0 & 81 & 0 0 & 40 & 1end {bmatrix}}}$		о₉ = о₃²	е₉ = е₃²		о₉
10	0	я	100	${displaystyle {egin {bmatrix} 1 & 49 & 1 0 & 100 & 0 0 & 50 & 0end {bmatrix}}}$		о₁₀ = оо_2,1о_1,2		е₁₀ = ее_2,1е_1,2
1	1	II	2	${displaystyle {egin {bmatrix} 1 & 0 & 1 0 & 2 & 0 0 & 1 & 0end {bmatrix}}}$		о_1,1 = j		е_1,1 = а
2	2	II	8	${displaystyle {egin {bmatrix} 1 & 3 & 1 0 & 8 & 0 0 & 4 & 0end {bmatrix}}}$		о_2,2 = j³		е_2,2 = а³
1	2	III	5	${displaystyle {egin {bmatrix} 1 & 2 & 0 0 & 5 & 0 0 & 2 & 1end {bmatrix}}}$		о_1,2 = п	е_1,2 = дп = pd		п
${displaystyle aequiv b}$ ${displaystyle (mathrm {mod} 2)}$		I, II или III	Т четное	${displaystyle {egin {bmatrix} 1 & {frac {T} {2}} - 1 & 1 0 & T & 0 0 & {frac {T} {2}} & 0end {bmatrix}}}$	...	о_{а, б}		е_{а, б}
${displaystyle aot Equiv b}$ ${displaystyle (mathrm {mod} 2)}$		I или III	Т странный	${displaystyle {egin {bmatrix} 1 & {frac {T-1} {2}} & 0 0 & T & 0 0 & {frac {T-1} {2}} & 1end {bmatrix}}}$	...	о_{а, б}	е_{а, б}		о_{а, б}

Примеры

Архимедовы и каталонские твердые тела

Исходный набор операторов Конвея может создавать все Архимедовы тела и Каталонские твердые вещества, с использованием Платоновы тела как семена. (Обратите внимание, что р оператор не требуется для создания обеих хиральных форм.)

Составные операторы

В усеченный икосаэдр, tI = zD, можно использовать в качестве начального числа для создания более визуально приятных многогранников, хотя они ни вершина ни лицо переходный.