WikiDer > Полярный момент инерции

Polar moment of inertia

Заметка: Полярный момент площади не следует путать с момент инерции, который характеризует объект угловое ускорение из-за крутящий момент.

В полярный момент инерции, также известный как второй полярный момент площади, это величина, используемая для описания устойчивости к крутильный деформация (отклонение), в цилиндрических объектах (или сегментах цилиндрического объекта) с инвариантом поперечное сечение и отсутствие значительного коробления или деформации вне плоскости.^[1] Это составная часть второй момент площади, связанные через теорема о перпендикулярной оси. Где планарный второй момент площади описывает сопротивление объекта прогибу (изгиб) под действием силы, приложенной к самолет параллельно центральной оси полярный второй момент площади описывает сопротивление объекта отклонению при воздействии момент наносится в плоскости, перпендикулярной центральной оси объекта (т. е. параллельно поперечному сечению). Похожий на планарный второй момент расчета площади ( ${displaystyle I_ {x}}$ , ${displaystyle I_ {y}}$ , и ${displaystyle I_ {xy}}$ ), полярный второй момент площади часто обозначается как ${displaystyle I_ {z}}$ . В некоторых инженерных учебниках и академических публикациях он также обозначается как ${displaystyle J}$ или же ${displaystyle J_ {z}}$ , этому обозначению следует уделить особое внимание, чтобы его не спутать с постоянная кручения, ${displaystyle J_ {t}}$ , используется для нецилиндрических объектов.

Проще говоря, полярный момент инерции - сопротивление вала или балки деформации при кручении в зависимости от его формы. Жесткость определяется только площадью поперечного сечения объекта и не зависит от его материального состава или модуль сдвига. Чем больше величина полярного момента инерции, тем больше сопротивление кручению объекта.

Определение

Схема, показывающая, как полярный момент инерции рассчитывается для произвольной формы вокруг оси

{displaystyle O}

. Где

{displaystyle ho}

радиальное расстояние до элемента

{displaystyle dA}

.

Заметка: Хотя термин моменты инерции используется для описания полярный и планарный вторые моменты площади, это прежде всего конструкция инженерное дело поля. Период, термин момент инерциив области физики и математики строго масса момент инерции, или второй момент массы, используется для описания сопротивления массивного объекта вращательному движению, а не его сопротивления крутильной деформации. В то время полярный и планарный вторые моменты инерции интегрируются по всем бесконечно малым элементам данного площадь в некотором двумерном сечении масса момент инерции суммируется по всем бесконечно малым элементам массы в трехмерном пространстве, занимаемом объектом. Проще говоря, полярный и планарный вторые моменты инерции указывают на жесткость, а масса момент инерции - это сопротивление вращательному движению массивного объекта.

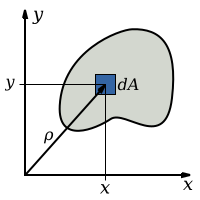
Уравнение, описывающее полярный момент инерции, представляет собой кратный интеграл по площади поперечного сечения, ${displaystyle A}$ , объекта.

{displaystyle J = iint limit _ {A} r ^ {2} dA}

куда ${displaystyle r}$ расстояние до элемента ${displaystyle dA}$ .

Подставляя ${displaystyle x}$ и ${displaystyle y}$ компоненты, используя теорема Пифагора:

{displaystyle J = iint limits _ {A} (x ^ {2} + y ^ {2}) dxdy}

{displaystyle J = iint limits _ {A} x ^ {2} dxdy + iint limits _ {A} y ^ {2} dxdy}

Учитывая планарный вторые моменты уравнений площади, где:

{displaystyle I_ {x} = iint limits _ {A} y ^ {2} dxdy}

{displaystyle I_ {y} = iint limits _ {A} x ^ {2} dxdy}

Показано, что полярный момент инерции можно описать как сумму ${displaystyle x}$ и ${displaystyle y}$ планарный моменты инерции, ${displaystyle I_ {x}}$ и ${displaystyle I_ {y}}$

{displaystyle здесь J = I_ {z} = I_ {x} + I_ {y}}

Это также показано в теорема о перпендикулярной оси.^[2] Для объектов с вращательной симметрией^[3], например, цилиндр или полая труба, уравнение можно упростить до:

{displaystyle J = 2I_ {x}}

или же

{displaystyle J = 2I_ {y}}

Для круглого сечения с радиусом ${displaystyle R}$ :

{displaystyle I_ {z} = int _ {0} ^ {2pi} int _ {0} ^ {R} r ^ {2} (r, dr, dphi) = {frac {pi R ^ {4}} {2 }}}

Единица измерения

В SI единица для полярный момент инерции, словно момент инерции площади, метры в четвертой степени (м⁴) и дюймов в четвертой степени (в⁴) в Обычные единицы США и имперские единицы.

Ограничения

Полярный момент инерции недостаточен для использования для анализа балок и валов с некруглым поперечным сечением из-за их тенденции к деформации при скручивании, вызывая деформации вне плоскости. В таких случаях постоянная кручения следует заменить, если включена соответствующая константа деформации для компенсации эффекта коробления. В нем есть статьи, в которых проводится различие между полярный момент инерции, ${displaystyle I_ {z}}$ , а крутильная постоянная, ${displaystyle J_ {t}}$ , больше не использую ${displaystyle J}$ для описания полярного момента инерции. ^[4]

В объектах со значительными изменениями поперечного сечения (вдоль оси приложенного крутящего момента), которые не могут быть проанализированы по сегментам, может потребоваться более сложный подход. Видеть Трехмерная эластичность.

Заявление

Хотя полярный момент инерции чаще всего используется для расчета угловое смещение объекта, подверженного воздействию момента (крутящий момент), нанесенного параллельно поперечному сечению, необходимо отметить, что указанное значение жесткости не имеет никакого отношения к сопротивлению скручиванию, обеспечиваемому объекту в зависимости от составляющих его материалов. Жесткость, обеспечиваемая материалом объекта, является характеристикой его модуль сдвига, ${displaystyle G}$ . Сочетание этих двух характеристик с длиной вала, ${displaystyle L}$ , можно рассчитать угловой прогиб вала, ${displaystyle heta}$ из-за приложенного крутящего момента, ${displaystyle T}$ :

{displaystyle heta = {frac {TL} {JG}}}

Как показано, чем больше модуль сдвига материала и полярный момент площади (т.е. больше площадь поперечного сечения), тем больше сопротивление крутильному прогибу.

Полярный момент площади фигурирует в формулах, описывающих крутильные стресс и угловое смещение.

Торсионные напряжения:

{displaystyle au = {гидроразрыв {T, r} {J_ {z}}}}

Где ${displaystyle au}$ напряжение сдвига при кручении, ${displaystyle T}$ приложенный крутящий момент, ${displaystyle r}$ - расстояние от центральной оси, а ${displaystyle J_ {z}}$ - полярный момент площади.

Заметка: В круглом валу напряжение сдвига максимальна на поверхности вала.

Пример расчета

Ротор современного паровая турбина.

Расчет паровая турбина Радиус вала для турбоагрегата:

Предположения:

Мощность на валу - 1000 МВт; это типично для большого атомная энергия растение.
Предел текучести из стали, из которой сделан вал (τ_{Уступать}) составляет: 250 × 10⁶ Н / м².
Электричество имеет частоту 50 Гц; это типичная частота в Европе. В Северной Америке частота 60 Гц. Это предполагает, что существует корреляция 1: 1 между скоростью вращения турбины и частотой электросети.

В угловая частота можно рассчитать по следующей формуле:

{displaystyle omega = 2pi f}

Крутящий момент, передаваемый валом, связан с мощность по следующему уравнению:

{displaystyle P = Tomega}

Таким образом, угловая частота равна 314,16. рад/s и крутящий момент 3.1831 × 10⁶ Н · м.

Максимальный крутящий момент составляет:

{displaystyle T_ {max} = {frac {au _ {max} J_ {z}} {r}}}

После замены полярный момент инерции получается следующее выражение:

{displaystyle r = {sqrt [{3}] {frac {2T_ {max}} {pi au _ {max}}}}}

В радиус является г = 0,200 м = 200 мм, или диаметр из 400 мм. Если добавить коэффициент безопасности 5 и пересчитывает радиус с допустимым напряжением, равным τ_адм=τ_{Уступать}/5 в результате получается радиус 0,343 м, или диаметром 690 мм, примерный размер вала турбоагрегата на атомной электростанции.

Сравнение полярного и массового моментов инерции

Полый цилиндр

Полярный момент инерции:

{displaystyle I_ {z} = {frac {pi left (D ^ {4} -d ^ {4} ight)} {32}}}

Момент инерции массы:

{displaystyle I_ {c} = I_ {z} ho l = {frac {pi ho lleft (D ^ {4} -d ^ {4} ight)} {32}}}

Цельный цилиндрПолярный момент инерции

{displaystyle I_ {z} = {frac {pi D ^ {4}} {32}}}

Момент инерции массы

{displaystyle I_ {c} = I_ {z} ho l = {frac {pi ho lD ^ {4}} {32}}}

куда:

${displaystyle d}$ это внутренний диаметр в метрах {м}
${displaystyle D}$ это Наружный диаметр в метрах {м}
${displaystyle I_ {c}}$ - момент инерции массы в кг · м²
${displaystyle I_ {z}}$ - полярный момент инерции в метрах в четвертой степени {m ^ 4}
${displaystyle l}$ длина цилиндра в метрах {м}
${displaystyle ho}$ - удельная масса в кг / м³

Смотрите также

внешняя ссылка

Кручение валов - engineeringtoolbox.com
Упругие свойства и модуль Юнга для некоторых материалов. - engineeringtoolbox.com
База данных свойств материалов^{[постоянная мертвая ссылка]} - matweb.com

[ugural-1] Ugural AC, Fenster SK. Повышенная прочность и прикладная эластичность. 3-е изд. Prentice-Hall Inc. Энглвуд Клиффс, Нью-Джерси. 1995 г. ISBN 0-13-137589-X.

[2] «Момент инерции. Определение с примерами». www.efunda.com.

[3] Обрегон, Хоакин (2012). Механическая симметрия. Авторский Дом. ISBN 978-1-4772-3372-6.

[4] галтор. «В чем разница между полярным моментом инерции, IPIP и постоянной кручения, JTJT поперечного сечения?».

[1]

[2]

[3]

[4]

Navigation