WikiDer > Предпочтительный кадр
В теоретическая физика, а предпочтительный или же привилегированный фрейм обычно особенный гипотетический точка зрения в которой законы физики может показаться идентифицируемым, отличным (более простым) от изображений в других кадрах.
В теориях, применяющих принцип относительности к инерционный движение, физика у всех одинакова инерциальные системы, и даже одинакова во всех кадрах по принципу общая теория относительности.
Предпочтительный фрейм в теории эфира
Эта секция нужны дополнительные цитаты для проверка. (Июль 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
В теориях, которые предполагают, что свет движется с фиксированной скоростью относительно неизменяемой и обнаруживаемой светоносный эфир, предпочтительным кадром был бы кадр, в котором этот эфир был бы неподвижен. В 1887 г. Майкельсон и Морли пытался определить состояние движения эфира. Для этого они предположили, что относительность Галилея удовлетворяется часами и линейками; то есть, что длина линейки и периоды часов неизменны при любом изменении системы отсчета Галилея. Согласно такой гипотезе эфир должен был наблюдаться.
Сравнивая измерения, сделанные в разных направлениях, и ища эффект, связанный с орбитальной скоростью Земли, их эксперимент, как известно, произвел нулевой результат. Как следствие, внутри Теория эфира Лоренца в Преобразование Галилея был заменен Преобразование Лоренца. Однако в теории эфира Лоренца предполагается существование необнаруживаемого эфира и выполняется принцип относительности. Теория была быстро заменена специальная теория относительности, который дал аналогичные формулы без существования ненаблюдаемого эфира. В обеих теориях все инерциальные системы отсчета физически эквивалентны. Точнее, при условии, что никакое явление не нарушает принцип относительности движения, нет средств для измерения скорости инерциального наблюдателя относительно возможной среды распространения квантовых волн.
Инерционные кадры предпочтительнее неинерциальных
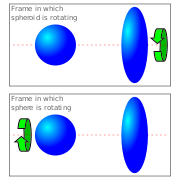
Хотя все инерциальные системы отсчета эквивалентны классическая механика и специальная теория относительностив этих теориях набор всех инерциальных систем отсчета имеет преимущество перед неинерциальными системами отсчета.[1]:10 Инерциальные системы отсчета являются привилегированными, потому что у них нет физики, причины которой находятся вне системы, в то время как неинерциальные системы отсчета имеют. Эйнштейн приводит следующий пример: предположим, что два равно-составлен упругие тела находятся в пространстве и удалены друг от друга, так что взаимодействием между ними можно пренебречь, и чье единственное относительное движение представляет собой равномерное жесткое вращение вокруг линии, соединяющей центры обоих тел (например, вращающиеся колеса вокруг ось). Одно из тел - это сфера, а другой - сфероид, раздавленная сфера. Наблюдаемое правильный физическая форма тел остается неизменной во всех кадрах. У невращающегося сфероида есть физика, причина которой лежит вне системы, ответственной за сжатие сфероида. Фрейм невращающейся сферы этого не делает, что делает его привилегированным, поскольку не требует внешних причин. Это относится ко всем инерциальным фреймам, которые имеют такое же преимущество.[1]:209 Эйнштейн продолжал развивать общая теория относительности и принцип эквивалентности, в которых инерциально-гравитационные системы отсчета больше не являются привилегированными,[1]:215—223 поскольку геодезические из пространство-время объяснить эти инерционно-гравитационные эффекты без внешней причины.[2]
Смотрите также
- Тесты специальной теории относительности
- Современные поиски нарушения Лоренца
- Космический микроволновый фон
- Тестовые теории специальной теории относительности
Рекомендации
- ^ а б c Ферраро, Рафаэль (2007), Пространство-время Эйнштейна: введение в специальную и общую теорию относительности, Springer Science & Business Media, Bibcode:2007esti.book ..... F, ISBN 9780387699462
- ^ Гилсон, Джеймс Г. (1 сентября 2004 г.), Принцип Маха II, arXiv:физика / 0409010, Bibcode:2004физика ... 9010G
- Эйнштейн: Относительность, специальная и общая теории (1954)