WikiDer > Пифагорейские средства - Википедия

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: «Пифагорейское означает» – Новости · газеты · книги · ученый · JSTOR (Июль 2019) (Узнайте, как и когда удалить этот шаблон сообщения)

Геометрическое построение среднего квадратичного и среднего Пифагора (двух чисел а и б). Гармоническое среднее обозначается   ЧАС, геометрическая по   грамм, арифметика   А и среднее квадратичное (также известное как среднеквадратичное значение) обозначается   Q.

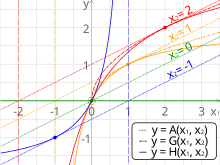
Сравнение средних арифметических, геометрических и гармонических пар чисел. Вертикальные пунктирные линии - асимптоты для гармонических средств.

В математике три классических Пифагорейские средства являются среднее арифметическое (AM), среднее геометрическое (GM), а гармоническое среднее (HM). Эти средства были изучены с пропорциями Пифагорейцы и более поздние поколения греческих математиков^[1] из-за их важности в геометрии и музыке.

Определение

Они определяются:

${ displaystyle { begin {align} operatorname {AM} left (x_ {1}, ; ldots, ; x_ {n} right) & = { frac {1} {n}} left (x_ {1} + ; cdots ; + x_ {n} right) [9pt] operatorname {GM} left (x_ {1}, ; ldots, ; x_ {n} справа) & = { sqrt [{n}] { left vert x_ {1} times , cdots , times x_ {n} right vert}} [9pt] operatorname {HM } left (x_ {1}, ; ldots, ; x_ {n} right) & = { frac {n} { displaystyle { frac {1} {x_ {1}}} + ; cdots ; + { frac {1} {x_ {n}}}}} end {align}}}$

Характеристики

Каждое означает, ${ textstyle operatorname {M}}$, имеет следующие свойства:

Первый заказ однородность

${ displaystyle operatorname {M} (bx_ {1}, , ldots, , bx_ {n}) = b operatorname {M} (x_ {1}, , ldots, , x_ {n} )}$

Инвариантность при обмене

${ displaystyle operatorname {M} ( ldots, , x_ {i}, , ldots, , x_ {j}, , ldots) = operatorname {M} ( ldots, , x_ { j}, , ldots, , x_ {i}, , ldots)}$

для любого ${ displaystyle i}$ и ${ displaystyle j}$.

Монотонный

${ displaystyle a$

Идемпотентность

${ Displaystyle forall х, ; М (х, х, ldots х) = х}$

Монотонность и идемпотентность вместе означают, что среднее значение набора всегда находится между крайними точками набора.

${ displaystyle min (x_ {1}, , ldots, , x_ {n}) leq operatorname {M} (x_ {1}, , ldots, , x_ {n}) leq max (x_ {1}, , ldots, , x_ {n})}$

Гармонические и арифметические средние являются взаимными двойниками друг друга для положительных аргументов:

${ displaystyle operatorname {HM} left ({ frac {1} {x_ {1}}}, , ldots, , { frac {1} {x_ {n}}} right) = { frac {1} { operatorname {AM} left (x_ {1}, , ldots, , x_ {n} right)}}}$

в то время как среднее геометрическое само по себе является двойственным:

${ displaystyle operatorname {GM} left ({ frac {1} {x_ {1}}}, , ldots, , { frac {1} {x_ {n}}} right) = { frac {1} { operatorname {GM} left (x_ {1}, , ldots, , x_ {n} right)}}}$

Неравенство средств

Геометрический доказательство без слов который Максимум (а,б) > среднее квадратичное или же среднеквадратичное значение (QM) > среднее арифметическое (ЯВЛЯЮСЬ) > среднее геометрическое (GM) > гармоническое среднее (HM) > мин (а,б) двух положительных чисел а и б ^[2]

У этих средств есть заказ (если все ${ displaystyle x_ {i}}$ положительные)

${ displaystyle min leq operatorname {HM} leq operatorname {GM} leq operatorname {AM} leq max}$

с равенством выполняется тогда и только тогда, когда ${ displaystyle x_ {i}}$ все равны.

Это обобщение неравенство средних арифметических и геометрических и частный случай неравенства для обобщенные средства. Доказательство следует из среднее арифметико-геометрическое неравенство, ${ Displaystyle OperatorName {AM} leq max}$, и взаимная двойственность (${ displaystyle min}$ и ${ displaystyle max}$ также взаимно двойственны друг другу).

Изучение пифагорейских средних тесно связано с изучением мажоризация и Шура-выпуклые функции. Гармонические и геометрические средние являются вогнутыми симметричными функциями своих аргументов и, следовательно, вогнутыми по Шуру, в то время как среднее арифметическое является линейной функцией своих аргументов, то есть как вогнутыми, так и выпуклыми.

Смотрите также

• Среднее арифметико-геометрическое
• Средний
• Золотое сечение

Рекомендации

1. ^ Хит, Томас. История древнегреческой математики.
2. ^ Если AC = а и BC = б. OC = ЯВЛЯЮСЬ из а и б, и радиус р = QO = OG.
   С помощью Теорема Пифагора, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
   Используя теорему Пифагора, OC² = OG² + GC² ∴ GC = √OC² - OG² = GM.
   С помощью похожие треугольники, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

внешняя ссылка

• Кантрелл, Дэвид В. «Пифагорейские средства». MathWorld.