WikiDer > Конвекция Рэлея-Бенара

Rayleigh–Bénard convection
Клетки Бенара.

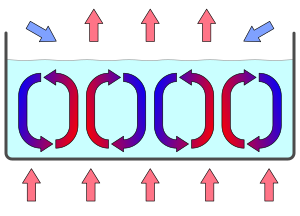
Конвекция Рэлея-Бенара это тип естественная конвекция, возникающий в плоском горизонтальном слое жидкости, нагреваемой снизу, в котором жидкость формирует регулярную структуру конвекционные ячейки известный как Клетки Бенара. Конвекция Бенара – Рэлея - одно из наиболее часто изучаемых явлений конвекции из-за ее аналитической и экспериментальной доступности.[1] Модели конвекции - это наиболее тщательно изученный пример самоорганизации. нелинейные системы.[1][2]

Плавучесть, и поэтому сила тяжести, ответственны за появление конвективных ячеек. Первоначальное движение - это подъем жидкости меньшей плотности из нагретого придонного слоя.[3] Этот апвеллинг спонтанно превращается в регулярную структуру клеток.

Физические процессы

Характеристики конвекции Бенара могут быть получены с помощью простого эксперимента, впервые проведенного Анри Бенар, французский физик, в 1900 году.

Развитие конвекции

Конвекционные ячейки в гравитационном поле

В экспериментальной установке используется слой жидкости, например вода, между двумя параллельными плоскостями. Высота слоя мала по сравнению с горизонтальным размером. Сначала температура нижней плоскости такая же, как и верхней. Тогда жидкость будет стремиться к равновесие, где его температура такая же, как и в окружающей его среде. (Оказавшись там, жидкость становится совершенно однородной: наблюдателю она может казаться одинаковой из любого положения. Это равновесие также асимптотически устойчивый: после локального временного возмущения внешней температуры он вернется в свое однородное состояние в соответствии с второй закон термодинамики).

Затем температура нижней плоскости немного повышается, в результате чего через жидкость проходит поток тепловой энергии. Система начнет иметь структуру теплопроводность: температура, а также плотность и давление будут линейно изменяться между нижней и верхней плоскостями. Будет установлен равномерный линейный градиент температуры. (Эта система может быть смоделирована статистическая механика).

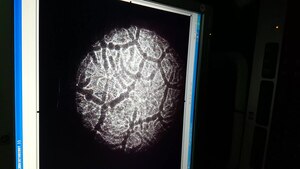
После установления проводимости микроскопическое случайное движение спонтанно упорядочивается на макроскопическом уровне, образуя конвективные ячейки Бенара с характерной корреляционной длиной.

Особенности конвекции

Моделирование конвекции Рэлея – Бенара в 3D.

Вращение ячеек стабильное и будет чередоваться от по часовой стрелке к против часовой стрелки по горизонтали; это пример спонтанное нарушение симметрии. Клетки Бенара метастабильный. Это означает, что небольшое возмущение не сможет изменить вращение ячеек, но большее может повлиять на вращение; они демонстрируют форму гистерезис.

Более того, детерминированный закон на микроскопическом уровне порождает недетерминированное расположение клеток: если эксперимент повторяется, конкретная позиция в эксперименте будет в ячейке по часовой стрелке в некоторых случаях и в ячейке против часовой стрелки в других. Микроскопические возмущения первоначальные условия достаточно, чтобы произвести недетерминированный макроскопический эффект. То есть в принципе невозможно рассчитать макроскопический эффект микроскопического возмущения. Эта неспособность предсказать условия на большом расстоянии и чувствительность к начальным условиям являются характеристиками хаотичный или же сложный системы (т.е. эффект бабочки).

турбулентная конвекция Рэлея – Бенара

Если бы температура нижней плоскости еще больше повысилась, конструкция стала бы более сложной в пространстве и времени; то турбулентный поток станет хаотичный.

Конвективные ячейки Бенара имеют тенденцию приближаться к правильным шестиугольным призмам, особенно при отсутствии турбулентности,[4][5][6] хотя некоторые экспериментальные условия могут привести к образованию правильных прямоугольных призм[7] или спирали.[8]

Конвективные ячейки Бенара не уникальны и обычно появляются только в конвекции, вызванной поверхностным натяжением. В общем, решения Рэлея и Пирсона[9] Анализ (линейная теория), предполагающий, что горизонтальный слой бесконечен, приводит к вырождению, что означает, что система может получить множество шаблонов. Предполагая однородную температуру на верхней и нижней пластинах, когда используется реалистичная система (слой с горизонтальными границами), форма границ будет определять узор. Чаще всего конвекция проявляется в виде валков или их наложения.

Неустойчивость Рэлея – Бенара.

Поскольку между верхней и нижней пластинами существует градиент плотности, сила тяжести пытается тянуть более холодную и более плотную жидкость сверху вниз. Этой гравитационной силе противостоит вязкая демпфирующая сила в жидкости. Баланс этих двух сил выражается безразмерным параметром, называемым Число Рэлея. Число Рэлея определяется как:

куда

Тты это температура верхней пластины
Тб это температура нижней пластины
L высота контейнера
грамм это ускорение силы тяжести
ν это кинематическая вязкость
α это Температуропроводность
β это Коэффициент теплового расширения.

По мере увеличения числа Рэлея силы гравитации становятся более доминирующими. При критическом числе Рэлея 1708[2] наступает неустойчивость и появляются конвективные ячейки.

Критическое число Рэлея можно получить аналитически для ряда различных граничных условий, выполнив анализ возмущений линеаризованных уравнений в устойчивом состоянии.[10] Самый простой случай - это случай двух свободных границ, который лорд Рэлей решил в 1916 году, получив Ra =27⁄4 π4 ≈ 657.51.[11] В случае жесткой границы внизу и свободной границы вверху (как в случае чайника без крышки) критическое число Рэлея получается равным Ra = 1100,65.[12]

Эффекты поверхностного натяжения

Основная статья: Эффект Марангони

При контакте свободной поверхности жидкости с воздухом плавучесть и поверхностное натяжение эффекты также будут играть роль в развитии конвективных моделей. Жидкости перетекают из мест с более низким поверхностным натяжением в места с более высоким поверхностным натяжением. Это называется Эффект Марангони. При подаче тепла снизу температура в верхнем слое будет показывать колебания температуры. С повышением температуры поверхностное натяжение уменьшается. Таким образом, боковой поток жидкости на поверхности будет иметь место,[13] из более теплых мест в более прохладные. Чтобы сохранить горизонтальную (или почти горизонтальную) поверхность жидкости, жидкость с более холодной поверхности будет опускаться. Этот поток более холодной жидкости способствует движущей силе конвекционных ячеек. Частный случай вариаций поверхностного натяжения, вызванных градиентом температуры, известен как термокапиллярная конвекция или конвекция Бенара – Марангони.

История и номенклатура

В 1870 году ирландско-шотландский физик и инженер Джеймс Томсон (1822–1892), старший брат Лорд Кельвин, наблюдали водяное охлаждение в кадке; он отметил, что мыльная пленка на поверхности воды была разделена, как если бы поверхность была выложена плиткой (мозаикой). В 1882 году он показал, что мозаика была вызвана наличием конвекционных ячеек.[14] В 1900 году французский физик Анри Бенар (1874–1939) независимо пришли к такому же выводу.[15] Эта модель конвекции, эффекты которой обусловлены исключительно температурным градиентом, была впервые успешно проанализирована в 1916 г. Лорд Рэйли (1842–1919).[16] Рэлей предположил граничные условия, при которых вертикальная составляющая скорости и температурное возмущение исчезают на верхней и нижней границах (идеальная теплопроводность). Эти предположения привели к тому, что анализ потерял всякую связь с экспериментом Анри Бенара. Это приводило к расхождениям между теоретическими и экспериментальными результатами до 1958 г., когда Джон Пирсон (1930–) переработали проблему на основе поверхностного натяжения.[9] Это то, что первоначально наблюдал Бенар. Тем не менее, в современном использовании термин «конвекция Рэлея – Бенара» относится к эффектам, обусловленным температурой, тогда как «конвекция Бенара – Марангони» относится конкретно к эффектам поверхностного натяжения.[1] Дэвис и Кошмидер предположили, что конвекцию по праву следует называть «конвекцией Пирсона – Бенара».[2]

Конвекцию Рэлея-Бенара также иногда называют «конвекцией Бенара-Рэлея», «конвекцией Бенара» или «конвекцией Рэлея».

Смотрите также

Рекомендации

  1. ^ а б c Гетлинг, А. В. (1998). Конвекция Бенара – Рэлея: структуры и динамика.. Всемирный научный. ISBN 978-981-02-2657-2.
  2. ^ а б c Кошмидер, Э. Л. (1993). Ячейки Бенара и вихри Тейлора. Кембридж. ISBN 0521-40204-2.
  3. ^ «Конвекция Рэлея – Бенара». Калифорнийский университет в Сан-Диего, Кафедра физики. Архивировано из оригинал 22 февраля 2009 г.
  4. ^ Конвекционные ячейки Рэлея-Бенара.с фотографиями из Лаборатории экологических технологий Национального управления океанических и атмосферных исследований Министерства торговли США.
  5. ^ http://www.edata-center.com/proceedings/1bb331655c289a0a,088ce8ea747789cd,59d115f133a4fd07.html
  6. ^ http://cat.inist.fr/?aModele=afficheN&cpsidt=17287579
  7. ^ http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=13973
  8. ^ http://www.psc.edu/science/Gunton/gunton.html
  9. ^ а б Пирсон, Дж. (1958). «О конвективных ячейках, вызванных поверхностным натяжением». Журнал гидромеханики. 4 (5): 489–500. Дои:10.1017 / S0022112058000616.
  10. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/benard.html
  11. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/node14.html
  12. ^ http://home.iitk.ac.in/~sghorai/NOTES/benard/node16.html
  13. ^ Устойчивые термокапиллярные потоки в двумерных пазах Journal of Fluid Mechanics, Vol. 121 (1982), стр. 163-186, DOI: 10.1017 / s0022112082001840, Асок К. Сен, Стивен Х. Дэвис
  14. ^ Томсон, Джеймс (1882). «Об изменении мозаичной структуры в некоторых жидкостях». Труды Философского общества Глазго. 8 (2): 464–468.
  15. ^ Бенар, Анри (1900). "Les Tourbillons Cellulaires dans une nappe liquid" [Клеточные вихри в листе жидкости]. Revue Générale des Sciences Pures et Appliquées (На французском). 11: 1261–1271, 1309–1328.
  16. ^ Рэлей, лорд (1916). «О конвективных потоках в горизонтальном слое жидкости, когда более высокая температура находится на нижней стороне». Философский журнал. 6-я серия. 32 (192): 529–546.

дальнейшее чтение

  • Субраманян Чандрасекар (1982). Гидродинамическая и гидромагнитная устойчивость. (Дувр). ISBN 0-486-64071-X
  • П.Г. Дразин и W.H. Рид (2004). Гидродинамическая устойчивость, второе издание (Cambridge University Press).
  • СРЕДНИЙ. Гетлинг (1998). Конвекция Рэлея-Бенара: структуры и динамика. (Мировой научный). ISBN 9810226578
  • E.L. Кошмидер (1993). Ячейки Бенара и вихри Тейлора (Издательство Кембриджского университета). ISBN 0-521-40204-2
  • Б. Зальцман (изд., 1962). Избранные статьи по теории тепловой конвекции со специальным приложением к планетной атмосфере Земли (Дувр).
  • Р. Х. Зейтунян (2009). Конвекция в жидкостях: рациональный анализ и асимптотическое моделирование (Спрингер).

внешняя ссылка