WikiDer > Эластичность резины
Эта статья ведущий раздел может быть слишком длинным для статьи. (Октябрь 2020) |
Эластичность резины относится к свойству сшитого каучука: он может растягиваться до 10 раз по сравнению с исходной длиной, а при отпускании почти возвращается к исходной длине. Это можно повторять много раз без видимого ухудшения качества резины. Каучук относится к более широкому классу материалов, называемых эластомерами, и их экономическое и технологическое значение трудно переоценить. Эластомеры сыграли ключевую роль в развитии новых технологий в 20 веке и внесли существенный вклад в мировую экономику. Эластичность резины возникает в результате нескольких сложных молекулярных процессов, и для ее объяснения требуются знания сложной математики, химии и статистической физики, особенно концепции энтропии. Энтропию можно рассматривать как меру тепловой энергии, которая хранится в молекуле. Обычные каучуки, такие как полибутадиен и полиизопрен (также называемый натуральным каучуком), производятся с помощью процесса, называемого полимеризацией. Очень длинные молекулы (полимеры) создаются последовательно путем добавления коротких звеньев основной цепи молекулы посредством химических реакций. Полимер каучука следует беспорядочной зигзагообразной траектории в трех измерениях, смешиваясь со многими другими молекулами каучука. Эластомер создается путем добавления нескольких процентов сшивающей молекулы, такой как сера. При нагревании сшивающая молекула вызывает реакцию, которая в какой-то момент химически соединяет (связывает) две молекулы каучука (сшивка). Поскольку молекулы каучука очень длинные, каждая из них участвует во многих сшивках со многими другими молекулами каучука, образуя непрерывную молекулярную сеть. При растяжении резиновой ленты некоторые сетевые цепочки вынуждены становиться прямыми, что вызывает уменьшение их энтропии. Именно это уменьшение энтропии приводит к возникновению упругой силы в цепочках сети.
История
После его появления в Европе из Нового Света в конце 15 века, натуральная резина (полиизопрен) рассматривался в основном как увлекательное любопытство. Самым полезным его применением была способность стирать карандашные следы на бумаге путем трения, отсюда и его название. Одно из его наиболее характерных свойств - небольшое (но заметное) повышение температуры, которое происходит при растяжении образца резины. Если дать возможность быстро втянуться, наблюдается равное охлаждение. Это явление привлекло внимание английского физика. Джон Гоф. В 1805 году он опубликовал несколько качественных наблюдений за этой характеристикой, а также за тем, как требуемая сила растяжения увеличивается с температурой.[1].
К середине девятнадцатого века теория термодинамика разрабатывался, и в этих рамках английский математик и физик Лорд Кельвин[2] показали, что изменение механической энергии, необходимой для растяжения образца резины, должно быть пропорционально повышению температуры. Позже это будет связано с изменением энтропия. Связь с термодинамикой была прочно установлена в 1859 году, когда английский физик Джеймс Джоуль опубликовали первые тщательные измерения повышения температуры, которое произошло при растяжении образца резины[3]. Эта работа подтвердила теоретические предсказания лорда Кельвина.
Лишь в 1838 году американский изобретатель Чарльз Гудьир обнаружили, что свойства натурального каучука можно значительно улучшить, добавив несколько процентов серы. Короткие серные цепочки образовывали химические поперечные связи между соседними полиизопрен молекулы. Жидкий натуральный каучук до сшивки состоит из очень длинных линейных цепей, содержащих тысячи изопрен магистральные узлы, соединенные голова к хвосту. Каждая цепочка проходит случайный путь через жидкость и контактирует с тысячами других ближайших цепей. При нагревании примерно до 150 ° C молекулы сшивающего агента (такие как сера или дикумилпероксид) могут разлагаться, и последующие химические реакции вызывают химическая связь между соседними цепями. В результате получается трехмерная молекулярная сеть. Все исходные цепи полиизопрена соединены во многих точках этими химическими связями (узлами сети), образуя единую гигантскую молекулу. Резинка - это одна молекула, как и латексная перчатка! Участки между двумя поперечными связями одной цепи называются сетевыми цепями и могут содержать до нескольких сотен изопреновых единиц. В натуральном каучуке каждая поперечная связь образует сетевой узел с четырьмя цепями, выходящими из него. Сеть - это sine qua non эластомеров.
Из-за огромного экономического и технологического значения каучука предсказание того, как молекулярная сеть реагирует на механические деформации, представляет непреходящий интерес для ученых и инженеров. Для теоретического понимания упругих свойств резины необходимо знать как физические механизмы, происходящие на молекулярном уровне, так и характер случайного блуждания резины. полимер цепочка определяет сеть. Физические механизмы, которые происходят в коротких участках полимерных цепей, создают упругие силы, а морфология сети определяет, как эти силы объединяются, чтобы произвести макроскопические стресс которые мы наблюдаем, когда образец резины деформируется, например подвергнутый деформация растяжения.
Модели на молекулярном уровне
На самом деле существует несколько физических механизмов, которые создают упругие силы в сетевых цепочках при растяжении резинового образца. Два из них возникают из-за изменений энтропии, а один связан с искажением валентных углов молекул вдоль основной цепи цепи. Эти три механизма сразу становятся видны, когда образец резины средней толщины растягивается вручную. Изначально резина кажется довольно жесткой, т.е. усилие необходимо увеличивать с большой скоростью по отношению к деформации. При промежуточных деформациях необходимое увеличение силы намного меньше, чтобы вызвать такое же растяжение. Наконец, когда образец приближается к пределу разрушения, его жесткость заметно возрастает. Наблюдатель замечает изменения в модуль упругости которые связаны с различными молекулярными механизмами. Эти области можно увидеть на рис. 1, типичном измерении зависимости напряжения от деформации для натурального каучука. Три механизма (обозначенные Ia, Ib и II) преимущественно соответствуют областям, показанным на графике. Концепция чего-либо энтропия приходит к нам из области математической физики, называемой статистическая механика который связан с изучением больших тепловых систем, например резиновые сети при комнатной температуре. Хотя подробное поведение составляющих цепочек является случайным и слишком сложным для изучения по отдельности, мы можем получить очень полезную информацию об их «среднем» поведении из статистического механического анализа большой выборки. Нет других примеров того, как изменения энтропии могут создавать силу в нашем повседневном опыте. Можно рассматривать энтропийные силы в полимерных цепях как результат тепловых столкновений, которые составляющие их атомы испытывают с окружающим материалом. Именно это постоянное толкание создает силу сопротивления (упругость) в цепях, поскольку они вынуждены становиться прямыми. Хотя растяжение образца резины является наиболее распространенным примером эластичности, оно также происходит при сжатии резины. Сжатие можно рассматривать как двумерное расширение, как при надувании воздушного шара. Молекулярные механизмы, создающие силу упругости, одинаковы для всех типов деформации.
Когда эти модели упругих сил сочетаются со сложной морфологией сети, невозможно получить простые аналитические формулы для прогнозирования макроскопического напряжения. Только с помощью численного моделирования на компьютерах можно зафиксировать сложное взаимодействие между молекулярными силами и морфологией сети, чтобы предсказать напряжение и окончательное разрушение образца резины при его деформации.
Парадигма молекулярного изгиба эластичности резины[4]
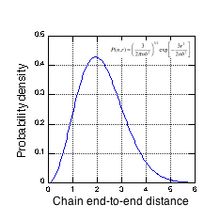
Парадигма молекулярного кинка исходит из интуитивного представления о том, что молекулярные цепи, составляющие натуральная резина (полиизопрен) сети ограничиваются окружающими цепями, чтобы оставаться в «трубе». Силы упругости, возникающие в цепи в результате некоторой приложенной деформации, распространяются по контуру цепи внутри этой трубки. На рис. 2 показано изображение четырехуглеродного изопренового звена основной цепи с дополнительным атомом углерода на каждом конце, что указывает на его связи с соседними звеньями в цепи. Он имеет три одинарные связи C-C и одну двойную связь. В основном, вращаясь вокруг одинарных связей C-C, полиизопреновая цепь случайным образом исследует свои возможные конформации. Участки цепи, содержащие от двух до трех изопреновых единиц, обладают достаточной гибкостью, чтобы их можно было считать статистически декоррелированными друг от друга. То есть нет никакой направленной корреляции вдоль цепи для расстояний, превышающих это расстояние, называемое Длина Куна. Эти непрямые области вызывают понятие "изломов" и фактически являются проявлением случайная прогулка характер цепи. Поскольку кинк состоит из нескольких звеньев изопрена, каждая из которых имеет три одинарные углерод-углеродные связи, существует множество возможных конформаций, доступных для кинка, каждая из которых имеет свою энергию и расстояние от конца до конца. В масштабе времени от секунд до минут только эти относительно короткие участки цепи, то есть перегибы, имеют достаточный объем, чтобы свободно перемещаться среди их возможных вращательных форм. Тепловые взаимодействия, как правило, поддерживают изгибы в состоянии постоянного потока, поскольку они совершают переходы между всеми их возможными вращательными формами. Поскольку изгибы находятся в тепловом равновесии, вероятность того, что изгиб находится в любой вращательной конформации, дается выражением Распределение Больцмана и мы можем связать энтропия с его сквозным расстоянием. Распределение вероятностей для сквозного расстояния Длина Куна примерно Гауссовский и определяется коэффициентами вероятности Больцмана для каждого состояния (вращательная конформация). По мере того как резиновая сетка растягивается, некоторые изгибы превращаются в ограниченное число более протяженных конформаций, имеющих большее расстояние от конца до конца, и именно в результате этого уменьшается энтропия, которая создает упругую силу вдоль цепи.
Есть три различных молекулярных механизма, которые создают эти силы, два из которых возникают в результате изменений энтропии, которые мы будем называть режимом низкого удлинения цепи, Ia[5] и режим умеренного удлинения цепи, Ib.[6] Третий механизм возникает при высоком удлинении цепи, так как она выходит за пределы исходного равновесного контура за счет искажения химических связей вдоль ее основной цепи. В этом случае возвращающая сила имеет пружинный характер и мы будем называть ее режимом II.[7] Было обнаружено, что три силовых механизма примерно соответствуют трем областям, наблюдаемым в экспериментах «растягивающее напряжение-деформация», показанных на рис.1.
Первоначальная морфология сети сразу после химического сшивания определяется двумя случайными процессами:[8][9] (1) вероятность того, что поперечная сшивка произойдет в любом изопреновом звене, и (2) характер случайного блуждания конформации цепи. Сквозное расстояние распределение вероятностей для фиксированной длины цепи, то есть фиксированного количества изопреновых звеньев, описывается случайным блужданием. Это совместное распределение вероятностей длин цепочек сети и сквозных расстояний между их узлами сшивки, которые характеризуют морфологию сети. Поскольку оба механизма молекулярной физики, которые производят упругие силы, и сложная морфология сети должны рассматриваться одновременно, простые аналитические модели упругости невозможны; явная 3-мерная численная модель[10][11][12] требуется для моделирования воздействия напряжения на представительный элемент объема сети.
Режим низкого удлинения цепи, Ia
Парадигма молекулярного перегиба представляет собой репрезентативную сетевую цепь как серию векторов, которые следуют по контуру цепи внутри ее трубки. Каждый вектор представляет собой равновесное расстояние от конца до конца перегиба. Фактический трехмерный путь цепи не имеет значения, поскольку предполагается, что все упругие силы действуют вдоль контура цепи. Помимо длины контура цепи, единственным важным параметром является ее извилистость, отношение длины контура к расстоянию от конца до конца. Предполагается, что по мере удлинения цепи в ответ на приложенную деформацию индуцированная упругая сила распространяется равномерно по ее контуру. Рассмотрим сетевую цепочку, конечные точки которой (сетевые узлы) более или менее выровнены с осью деформации растяжения. Когда к образцу резины прикладывается начальная деформация, узлы сети на концах цепочки начинают раздвигаться, и все векторы перегиба по контуру растягиваются одновременно. Физически приложенная деформация вынуждает изгибы выходить за пределы их тепловое равновесие сквозные расстояния, вызывающие уменьшение их энтропии. Увеличение свободной энергии, связанное с этим изменением энтропии, приводит к возникновению (линейной) упругой силы, противодействующей деформации. Силовая постоянная для режима низкой деформации может быть оценена путем отбора проб молекулярная динамика (MD) траектории излома, то есть короткие цепочки, состоящие из 2-3 единиц изопрена, при соответствующих температурах, например 300К.[5] Путем взятия множества отсчетов координат в ходе моделирования можно получить распределения вероятностей сквозного расстояния для перегиба. Поскольку эти распределения (которые оказываются примерно Гауссовский) напрямую связаны с количеством состояний, мы можем связать их с энтропией излома на любом сквозном расстоянии. Путем численного дифференцирования распределения вероятностей изменение энтропии и, следовательно, свободная энергия, относительно расстояния перегиба от конца до конца. Модель сил для этого режима оказывается линейной и пропорциональной температуре, деленной на извилистость цепи.
Режим умеренного удлинения цепи, Ib
В какой-то момент в режиме низкого растяжения, то есть когда все изгибы цепи растягиваются одновременно, становится энергетически более выгодным иметь один изгиб, переходящий в расширенную конформацию, чтобы растянуть цепь дальше. Приложенная деформация может заставить одиночный изопреновый элемент внутри изгиба принять расширенную конформацию, немного увеличивая расстояние от конца до конца цепи, а энергия, необходимая для этого, меньше энергии, необходимой для продолжения одновременного расширения всех изломов. . Многочисленные эксперименты[13] настоятельно предполагают, что растяжение резиновой сети сопровождается уменьшением энтропии. Как показано на рис. 2, изопреновый элемент имеет три одинарные связи C-C, и существует два или три предпочтительных угла поворота (ориентации) этих связей, которые имеют минимальные значения энергии. Из 18 разрешенных[6] вращательные конформации, только 6 имеют увеличенные расстояния от конца до конца, и принуждение звеньев изопрена в цепи находиться в некотором подмножестве расширенных состояний должно уменьшить количество вращательных конформаций, доступных для теплового движения. Именно это уменьшение количества доступных состояний вызывает уменьшение энтропии. По мере того как цепь продолжает выпрямляться, все изопреновые звенья в цепи в конечном итоге вынуждены принимать расширенные конформации, и цепь считается «натянутой». Силовая постоянная для удлинения цепи может быть оценена по результирующему изменению свободной энергии, связанному с этим изменением энтропии.[6] Как и в случае режима Ia, силовая модель для этого режима линейна и пропорциональна температуре, деленной на извилистость цепи.
Режим высокого удлинения цепи, II
Когда все изопреновые единицы в сетевой цепи вынуждены находиться всего в нескольких расширенных вращательных конформациях, цепь становится натянутой. Его можно рассматривать как разумно прямой, за исключением зигзагообразного пути, который связи C-C образуют по контуру цепи. Однако дальнейшее удлинение по-прежнему возможно за счет искажений связи, например увеличения угла связи, удлинения связи и двугранный угол вращения. Эти силы подобны пружине и не связаны с изменениями энтропии. Натянутую цепь можно удлинить только примерно на 40%. В этот момент сила, действующая вдоль цепи, достаточна для механического разрыва ковалентной связи C-C. Этот предел растягивающей силы был рассчитан[7] через квантовая химия моделирования и составляет примерно 7 нН, что примерно в тысячу раз больше, чем энтропийные цепные силы при низкой деформации. Углы между соседними связями C-C основной цепи в изопреновом звене варьируются в пределах примерно 115-120 градусов, а силы, связанные с поддержанием этих углов, довольно велики, поэтому внутри каждого звена основа цепи всегда следует зигзагообразным путем, даже при разрыве связи. Этот механизм объясняет резкий подъем упругого напряжения, наблюдаемый при высоких деформациях (рис. 1).
Морфология сети
Хотя сеть полностью описывается только двумя параметрами (количеством узлов сети на единицу объема и длиной статистической декорреляции полимера, Длина Куна), способ соединения цепочек на самом деле довольно сложен. Длина цепочек сильно различается, и большинство из них не подключены к ближайшему соседнему узлу сети. И длина цепи, и расстояние от конца до конца описываются распределениями вероятностей. Термин «морфология» относится к этой сложности. Если сшивающий агент тщательно перемешан, существует равная вероятность того, что любой изопреновый элемент станет сетевым узлом. Для дикумилпероксида эффективность сшивки в натуральном каучуке равна единице.[14], но это не относится к сере.[15] Первоначальная морфология сети продиктована двумя случайными процессами: вероятностью возникновения поперечной сшивки в любой изопреновой единице и характером марковского случайного блуждания конформации цепи.[8][9] Функция распределения вероятности того, насколько далеко один конец цепи может «отклоняться» от другого, генерируется с помощью марковской последовательности.[16] Эта условная функция плотности вероятности связывает длину цепи в единицах длины Куна на сквозное расстояние :
(1)
Вероятность того, что какое-либо изопреновое звено станет частью сшивающего узла, пропорциональна отношению концентраций сшивающих молекул (например, дикумилпероксида) к изопреновым звеньям:
Фактор два возникает из-за того, что две изопреновые единицы (по одной от каждой цепи) участвуют в поперечной сшивке. В вероятность для поиска цепи, содержащей единицы изопрена рассчитываются по:
(3)
где Уравнение можно понимать как просто вероятность того, что изопреновая единица НЕ является поперечной связью (1-пИкс) в N-1 последовательные единицы по цепочке. поскольку P (N) уменьшается с N, более короткие цепи более вероятны, чем более длинные. Обратите внимание, что количество статистически независимых сегментов основной цепи не совпадает с количеством изопреновых единиц. Для сетей из натурального каучука длина Куна содержит около 2,2 единиц изопрена, поэтому . Это продукт уравнений (1) и (3) ( совместное распределение вероятностей), который связывает длину сетевой цепочки () и сквозное расстояние () между конечными узлами перекрестной связи:
(4)
Сложную морфологию сети из натурального каучука можно увидеть на рис. 3, на котором показана зависимость плотности вероятности от сквозного расстояния (в единицах среднего расстояния между узлами) для «средней» цепи. Для обычной экспериментальной плотности сшивки 4х1019 см−3, средняя цепь содержит около 116 изопреновых единиц (52 длины Куна) и имеет контурную длину около 50 нм. Рис. 3 показывает, что значительная часть цепочек охватывает несколько интервалов между узлами, т. Е. Концы цепочек перекрывают другие цепочки сети. Натуральный каучук, поперечно сшитый перекисью дикумила, имеет тетрафункциональные поперечные связи, то есть каждый узел поперечной связи имеет 4 исходящие от него сетевые цепи. В зависимости от их начальной извилистости и ориентации их конечных точек по отношению к оси деформации каждая цепь, связанная с активным узлом сшивки, может иметь различную упругую силовая постоянная поскольку он противостоит приложенной нагрузке. Чтобы сохранить равновесие сил (нулевое результирующее усилие) на каждом узле поперечной связи, узел может быть вынужден двигаться в тандеме с цепью, имеющей наивысшую постоянную силы для удлинения цепи. Именно это сложное движение узлов, возникающее из-за случайного характера морфологии сети, делает изучение механических свойств резиновых сетей столь трудным. По мере того как сеть деформируется, появляются пути, составленные из этих более протяженных цепей, которые охватывают весь образец, и именно эти пути несут большую часть напряжения при высоких деформациях.
Имитационная модель сети
Для расчета упругого отклика резинового образца три модели цепных сил (режимы Ia, Ib и II) и морфология сети должны быть объединены в микромеханической модели сети.[10][11][12] Используя совместное распределение вероятностей в уравнении (4) и модели расширения силы, можно разработать численные алгоритмы как для построения точного представительного элемента объема сети, так и для моделирования результирующего механического напряжения, когда он подвергается деформации. Алгоритм итерационной релаксации используется для поддержания приблизительного равновесия сил в каждом узле сети при приложении напряжения. Когда силовая постоянная, полученная для перегибов, содержащих 2 или 3 единицы изопрена (примерно одна длина Куна), используется в численном моделировании, предсказанное напряжение согласуется с экспериментами. Результаты такого расчета[15] показаны на рис.1 (пунктирная красная линия) для сшитого серой натурального каучука и сравниваются с экспериментальными данными.[17] (сплошная синяя линия). Это моделирование также предсказывает резкий скачок напряжения по мере натяжения цепей сети и, в конечном итоге, разрушение материала из-за разрыва связи. В случае сшитого серой натурального каучука связи S-S в поперечных связях намного слабее, чем связи C-C в основной цепи цепи, и являются точками отказа сети. Плато в смоделированном напряжении, начиная с деформации около 7, является предельным значением для сети. Напряжения более 7 МПа не поддерживаются, и сеть выходит из строя. Вблизи этого предела напряжения моделирование предсказывает[12] что менее 10% цепей натянуты, т.е. в режиме высокого удлинения цепи и менее 0,1% цепей разорваны. Хотя очень низкая доля разрыва может показаться удивительной, это не противоречит нашему опыту растягивания резиновой ленты до ее разрыва. Эластичный отклик резины после разрыва практически не отличается от оригинала.
Эксперименты
Изменение растягивающего напряжения в зависимости от температуры
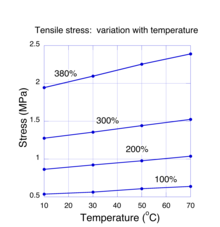
Для молекулярных систем, находящихся в тепловом равновесии, добавление энергии. е. г. механической работой может вызвать изменение энтропии. Это известно из теорий термодинамики и статистической механики. В частности, обе теории утверждают, что изменение энергии должно быть пропорционально изменению энтропии, умноженному на абсолютную температуру. Это правило действует только до тех пор, пока энергия ограничивается тепловыми состояниями молекул. Если образец каучука растянут достаточно далеко, энергия может находиться в нетепловых состояниях, таких как искажение химических связей, и это правило не применяется. Теория предсказывает, что при деформации от низкой до умеренной, требуемая сила растяжения связана с изменением энтропии в сетевых цепочках. Если это верно, то мы ожидаем, что сила, необходимая для растяжения образца до некоторого значения деформации, должна быть пропорциональна температуре образца. Измерения, показывающие, как растягивающее напряжение в растянутом образце резины изменяется в зависимости от температуры, показаны на рис. 4. В этих экспериментах[18]деформация растянутого образца резины фиксировалась при изменении температуры от 10 до 70 градусов Цельсия. Видно, что для каждого значения фиксированной деформации растягивающее напряжение изменялось линейно (с точностью до экспериментальной ошибки). Эти эксперименты предоставляют наиболее убедительные доказательства того, что изменения энтропии являются фундаментальным механизмом эластичности резины. Положительное линейное поведение напряжения в зависимости от температуры иногда приводит к ошибочному представлению о том, что резина имеет отрицательное значение. коэффициент температурного расширения, т.е. длина образца сокращается при нагревании. Эксперименты[19] убедительно показали, что, как и почти все другие материалы, коэффициент теплового расширения натурального каучука положительный.
Скорость возврата

Когда мы растягиваем кусок резины, например резинку, мы замечаем, что она деформируется равномерно по длине. Каждый элемент по длине имеет тот же коэффициент расширения, что и весь образец. Если мы отпустим один конец, образец очень быстро вернется к своей исходной длине, слишком быстро, чтобы наш глаз мог разрешить процесс. Наше интуитивное ожидание состоит в том, что он вернется к своей исходной длине таким же образом, как когда он был растянут, т.е. е. равномерно. Однако этого не происходит. Экспериментальные наблюдения Mrowca et al.[20] показать удивительное поведение.Чтобы зафиксировать чрезвычайно быструю динамику ретракции, они использовали умный экспериментальный метод, разработанный Экснером и Стефаном.[21] в 1874 году, задолго до изобретения высокоскоростных электронных измерительных устройств. Их метод заключался в использовании быстро вращающегося стеклянного цилиндра, который после покрытия ламповой сажей помещался рядом с растянутым образцом резины. Щупы, прикрепленные к середине и свободному концу резинового образца, удерживались в контакте со стеклянным цилиндром. Затем, когда свободный конец резины защелкнулся, щупы образовали спиральные траектории в черном покрытии вращающегося цилиндра. Регулируя скорость вращения цилиндра, они могли регистрировать положение щупов менее чем за один полный оборот. Траектории переносили на график, катая цилиндр по влажной промокательной бумаге. Метка, оставленная стилусом, появилась на бумаге в виде белой линии (без черной лампы). Их данные, представленные в виде графика на рис. 5, показывают положение конечных и средних точек щупов по мере того, как образец быстро сокращается до своей исходной длины. Первоначально образец был растянут на 9,5 дюймов за пределы его естественной длины, а затем отпущен. Щупы вернулись в исходное положение (смещение 0 дюймов) чуть более чем за 6 мс. Линейное поведение смещения в зависимости от времени указывает на то, что после кратковременного ускорения и конец, и средняя точка образца резко повернулись назад с постоянной скоростью около 50 м / с или 112 миль в час. Однако стилус средней точки не начинал двигаться примерно через 3 мс после отпускания конца. Очевидно, что процесс ретракции распространяется как волна, начиная со свободного конца. При больших растяжениях часть энергии, запасенной в растянутой цепочке сети, обусловлена изменением ее энтропии, но большая часть энергии сохраняется в искажениях связей (режим II, выше), которые не связаны с изменением энтропии. Если предположить, что вся накопленная энергия преобразуется в кинетическую, скорость втягивания может быть вычислена непосредственно из известного уравнения сохранения E = ½ мВ.2. Численное моделирование[11], основанный на парадигме молекулярного кинка, предсказать скорости, согласующиеся с этим экспериментом.
Исторические подходы к теории упругости
Юджин Гут и Хьюберт М. Джеймс предложил энтропийное происхождение эластичности резины в 1941 году.[22]
Термодинамика
Температура необычным образом влияет на эластичность эластомеров. Когда предполагается, что эластомер находится в растянутом состоянии, нагрев заставляет их сжиматься. И наоборот, охлаждение может вызвать расширение.[23]Это можно наблюдать с помощью обычного резинка. Если натянуть резинку, она будет выделять тепло (прижать ее к губам), а отпускание после того, как она была растянута, приведет к поглощению тепла, в результате чего окружающее пространство станет холоднее. Это явление можно объяснить тем, что Свободная энергия Гиббса. Перестановка Δг= ΔЧАС−ТΔS, где г это свободная энергия, ЧАС это энтальпия, и S это энтропия, мы получаем ТΔS= ΔЧАС−Δг. Поскольку растяжение происходит неспонтанно и требует внешней работы, ТΔS должно быть отрицательным. поскольку Т всегда положительный (никогда не достигнет полный ноль), ΔS должен быть отрицательным, что означает, что резина в ее естественном состоянии более запутана (с большей микросостояния), чем когда он находится под напряжением. Таким образом, при снятии напряжения реакция носит спонтанный характер, ведущий к Δг быть отрицательным. Следовательно, охлаждающий эффект должен приводить к положительному значению ΔH, поэтому ΔS там будет положительно.[24][25]
В результате эластомер ведет себя как идеальный одноатомный газ, поскольку (с хорошим приближением) эластичные полимеры не хранят любую потенциальную энергию в растянутых химических связях или в упругой работе, совершаемой при растяжении молекул, когда над ними совершается работа. Вместо этого вся работа, проделанная с резиной, «высвобождается» (не сохраняется) и немедленно проявляется в полимере в виде тепловой энергии. Точно так же вся работа, которую резинка выполняет с окружающей средой, приводит к исчезновению тепловой энергии, необходимой для совершения этой работы (резинка становится холоднее, как расширяющийся газ). Это последнее явление является решающим признаком того, что способность эластомера выполнять работу зависит (как и в случае с идеальным газом) только от соображений изменения энтропии, а не от какой-либо запасенной (то есть потенциальной) энергии в полимерных связях. Вместо этого энергия для выполнения работы полностью исходит из тепловой энергии, и (как в случае расширяющегося идеального газа) только положительное изменение энтропии полимера позволяет эффективно преобразовать его внутреннюю тепловую энергию (теоретически 100%) в работу. .
Теории полимерных цепей
Используя теорию эластичности резины, можно рассматривать полимерную цепь в поперечно-сшитой сети как энтропийный источник. Когда цепь растягивается, энтропия значительно уменьшается, потому что доступно меньше конформаций.[26] Следовательно, существует восстанавливающая сила, которая заставляет полимерную цепь возвращаться в ее равновесное или нерастянутое состояние, такое как конфигурация случайной катушки с высокой энтропией, после того, как внешняя сила устранена. Это причина, по которой резинки возвращаются в исходное состояние. Две распространенные модели эластичности резины - это модель цепи со свободными сочленениями и модель червеобразной цепи.
Модель цепи со свободным сочленением
Свободно соединенная цепь, также называемая идеальной цепью, следует модель случайного блуждания. Микроскопически трехмерное случайное блуждание полимерной цепи предполагает, что общее расстояние от конца до конца выражается через направления x, y и z:
В модели - длина жесткого отрезка, это количество отрезков длины , - расстояние между неподвижным и свободным концом, а "длина контура" или . Выше температуры стеклования полимерная цепь колеблется и меняется со временем. Распределение вероятностей цепочки - это произведение распределений вероятностей отдельных компонентов, заданное следующим распределением Гаусса:
Следовательно, среднее по ансамблю сквозное расстояние - это просто стандартный интеграл распределения вероятностей по всему пространству. Обратите внимание, что движение может быть вперед или назад, поэтому чистое среднее будет ноль. Однако в качестве полезной меры расстояния можно использовать среднеквадратическое значение.
Теория эластичности резины Флори указывает на то, что эластичность резины имеет в основном энтропийное происхождение. Используя следующие основные уравнения для Свободная энергия Гельмгольца и обсуждение энтропии, сила, возникающая в результате деформации резиновой цепи из ее исходной нерастянутой формы, может быть получена. В - количество конформаций полимерной цепи. Поскольку деформация не связана с изменением энтальпии, изменение свободной энергии можно просто рассчитать как изменение энтропии. Можно заметить, что уравнение силы напоминает поведение пружины и следует Закон Гука:, где F - сила, k - жесткость пружины, x - расстояние. Обычно, неогуковская модель могут использоваться для сшитых полимеров для прогнозирования их отношений напряжения и деформации:
Отметим, что коэффициент упругости зависит от температуры. Если мы увеличим температуру резины, коэффициент упругости также возрастет. Это причина того, что резина при постоянном напряжении дает усадку при повышении температуры.
Мы можем дополнительно расширить теорию Флори до макроскопической точки зрения, где обсуждается объемный резиновый материал. Предположим, что исходный размер резинового материала равен , и , деформированная форма может быть выражена путем применения индивидуального коэффициента удлинения к длине (, , ). Таким образом, с микроскопической точки зрения деформированная полимерная цепь также может быть выражена с помощью коэффициента удлинения: , , . Тогда изменение свободной энергии из-за деформации можно выразить следующим образом:
Предположим, что резина сшита и изотропна, модель случайного блуждания дает , и распределяются по нормальному распределению. Следовательно, они равны в пространстве, и все они составляют 1/3 от общего сквозного расстояния цепи: . Подключив приведенное выше изменение уравнения свободной энергии, легко получить:
Изменение свободной энергии на единицу объема равно:
где - количество нитей в сети, индекс означает "деформация", , которая представляет собой объемную плотность полимерных цепей, которое представляет собой отношение между сквозным расстоянием цепи и теоретическим расстоянием, которое подчиняется статистике случайного блуждания. Если предположить несжимаемость, произведение коэффициентов растяжения равно 1, что означает отсутствие изменения объема:.
Практический пример: Одноосная деформация:
В одноосно деформированной резине, потому что мы предполагаем . Итак, предыдущее уравнение свободной энергии на объем:
В инженерное напряжение (по определению) - это первая производная энергии с точки зрения коэффициента растяжения, что эквивалентно концепции деформации:
и Модуль для младших определяется как производная напряжения по отношению к деформации, которая измеряет жесткость резины в лабораторных экспериментах.
где , - массовая плотность цепи, представляет собой среднечисловую молекулярную массу сетевой нити между поперечными связями. Здесь этот тип анализа связывает термодинамическую теорию упругости резины с экспериментально измеряемыми параметрами. Кроме того, это дает представление о сшиваемости материалов.
Модель червеобразной цепи
Модель червеобразной цепи (WLC) учитывает энергию, необходимую для изгиба молекулы. Переменные такие же, за исключением того, что , длительность сохранения заменяет . Тогда сила следует этому уравнению:
Следовательно, когда нет расстояния между концами цепочки (р= 0), сила, необходимая для этого, равна нулю, а для полного удлинения полимерной цепи (), требуется бесконечная сила, что интуитивно понятно. Графически сила начинается в начале координат и сначала линейно увеличивается с увеличением . Затем сила достигает плато, но в конечном итоге снова увеличивается и приближается к бесконечности по мере приближения длины цепи. .
Смотрите также
использованная литература
- ^ Proc. Лит. и Фил. Soc., Манчестер, 2-я сер., 1, 288 (1805)
- ^ Лорд Кельвин, Quarterly J. Math., 1, 57 (1857)
- ^ Джоуль JP. О термодинамических свойствах твердых тел. Фил Trans R Soc Lond. 1859; 149: 91–131.
- ^ Д. Э. Хэнсон и Дж. Л. Барбер, Contemporary Physics 56 (3), 319-337 (2015), LAPR-2015-022971
- ^ а б Д. Э. Хэнсон и Р. Л. Мартин, Журнал химической физики 133, 084903 (084908 стр.) (2010)
- ^ а б c Д. Э. Хэнсон, Дж. Л. Барбер и Г. Субраманиан, Journal of Chemical Physics 139 (2013), LAPR-2014-018991
- ^ а б Д. Э. Хэнсон и Р. Л. Мартин, Журнал химической физики 130, 064903 (2009), LAPR-2009-006764
- ^ а б П. Флори, Н. Рабджон и М. Шаффер, Journal of Polymer Science 4, 435-455 (1949)
- ^ а б Д. Э. Хэнсон, Журнал химической физики 134, 064906 (064906 стр.) (2011)
- ^ а б Д. Э. Хэнсон, Полимер 45 (3), 1058-1062 (2004)
- ^ а б c Д. Э. Хэнсон, Journal of Chemical Physics 131, 224904 (224905 стр.) (2009)
- ^ а б c Д. Э. Хэнсон и Дж. Л. Барбер, Моделирование и моделирование в материаловедении и инженерии 21 (2013), LAPR-2013-017962
- ^ Дж. П. Джоуль, Фил. Пер. R. Soc. Лондон, 149, 91–131 (1859)
- ^ Л.Д. Заем, чистая заявка. Chem. 30 (1972)
- ^ а б Д. Э. Хэнсон, Дж. Л. Барбер, Phys. Chem. Chem. Phys. 20, 8460 (2018), LAPR-2018-029488
- ^ Марков А.А., Изв. Peterb. Акад. 4 (1), 61-80 (1907)
- ^ L.R.G. Treloar, Trans. Faraday Soc., 40, 0059 (1944).
- ^ а б Р. Л. Энтони, Р. Х. Кастон, Юджин Гут, J. Phys. Chem. 46, 8, (1942)
- ^ Л. А. Вуд и Г. Мартин, Журнал исследований Национального бюро стандартов-A. Физика и химия Том 68А, № 3 (1964).
- ^ а б Б. А. Мрова, С. Л. Дарт и Э. Гут, Physical Review 66, 30 (1944).
- ^ Дж. С. Уитби, «Плантационный каучук и испытания каучука», Longmans and Green, Лондон, 1920. стр. 461.
- ^ Гут, Юджин; Джеймс, Хьюберт М. (май 1941 г.). «Упругие и термоупругие свойства резиноподобных материалов». Ind. Eng. Chem. 33 (5): 624–629. Дои:10.1021 / ie50377a017.
- ^ «Термодинамика резиновой ленты», Американский журнал физики, 31 (5): 397–397, май 1963 г., Bibcode:1963AmJPh..31..397T, Дои:10.1119/1.1969535
- ^ Резинки и тепло, http://scifun.chem.wisc.edu/HomeExpts/rubberband.html, цитируя Шахашири (1983)
- ^ Шахашири, Бассам З. (1983), Химические демонстрации: пособие для учителей химии, 1, Мэдисон, Висконсин: Издательство Висконсинского университета, ISBN 978-0-299-08890-3
- ^ L.R.G. Treloar (1975), Физика эластичности резины, Издательство Оксфордского университета, ISBN 9780198570271






![{displaystyle p_ {x} = 2 {frac {[{ext {cross-link}}]} {[{ext {isoprene}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d34c22b316c310d5cb7774b9201509cafc52ac)