WikiDer > Салинон
В салинон (что означает «солонка» по-гречески) - это геометрическая фигура который состоит из четырех полукруги. Впервые он был представлен в Книга лемм, работа, приписываемая Архимед.[1]
строительство
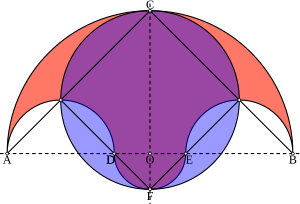
Позволять О быть источником на Декартова плоскость. Позволять А, D, E, и B быть четырьмя точками на линии в указанном порядке, причем О биссектриса AB. Позволять ОБЪЯВЛЕНИЕ = EB. Полукруги нарисованы над линией AB с участием диаметры AB, ОБЪЯВЛЕНИЕ, и EB, а внизу проведен еще один полукруг диаметром DE. Салинон - это фигура, ограниченная этими четырьмя полукругами.[2]
Свойства
Площадь
Архимед ввел салинон в Книга лемм применяя Книгу II, предложение 10 Евклида Элементы. Архимед заметил, что «площадь фигуры, ограниченная окружностями всех полукругов, [равна] площади круга на CF как диаметра».[3]
А именно площадь салинона составляет:
Доказательство
Пусть радиус середина из ОБЪЯВЛЕНИЕ и EB обозначается как г и ЧАСсоответственно. Следовательно, AG = GD = EH = HB = р1. Потому что ДЕЛАТЬ, Из, и OE все радиусы одного полукруга, ДЕЛАТЬ = Из = OE = р2. При добавлении сегмента AG + GD + ДЕЛАТЬ = OE + EH + HB = 2р1 + р2. поскольку AB диаметр салинона, CF линия симметрии. Поскольку все они являются радиусами одного полукруга, АО = BO = CO = 2р1 + р2.
Позволять п быть центром большого круга. Потому что CO = 2р1 + р2 и Из = р2, CF = 2р1 + 2р2. Следовательно, радиус круга равен р1 + р2. Площадь круга = π (р1 + р2)2.
Позволять Икс = р1 и у = р2. Площадь полукруга диаметром AB, обозначаемый , является:
Площадь полукруга диаметром DE является:
Площадь каждого из полукругов с диаметрами ОБЪЯВЛЕНИЕ и EB является
Следовательно, площадь салинона составляет:
Q.E.D.[4]
Арбелос
Если указывает D и E сходиться с О, это сформировало бы арбелос, еще одно творение Архимеда, с симметрия вдоль ось Y.[3]
Смотрите также
использованная литература
- ^ а б Вайсштейн, Эрик В. ""Салинон. "Из MathWorld - веб-ресурс Wolfram". Получено 2008-04-14.
- ^ Нельсен, Роджер Б. (2002). «Доказательство без слов: площадь солончака». Математический журнал (PDF). п. 130.
- ^ а б Богомольный Александр. "Салинон: Из книги лемм Архимеда из сборника интерактивных математических задач и головоломок". из интерактивной математики и головоломок. Получено 2008-04-15.
- ^ Умбергер, Шеннон. «Эссе № 4 - Арбелос и Салинон». Получено 2008-04-18.
внешние ссылки
- L’arbelos. Партия II Хамза Хелиф в www.images.math.cnrs.fr из CNRS