WikiDer > Сегментированная регрессия
| Часть серии по |
| Регрессивный анализ |
|---|
 |
| Модели |
| Оценка |
| Фон |
Сегментированная регрессия, также известный как кусочная регрессия или регрессия сломанной палки, это метод в регрессивный анализ в которой независимая переменная разбивается на интервалы, и каждому интервалу соответствует отдельный отрезок. Сегментированный регрессионный анализ также может выполняться на многомерных данных путем разделения различных независимых переменных. Сегментированная регрессия полезна, когда независимые переменные, сгруппированные в разные группы, демонстрируют разные отношения между переменными в этих регионах. Границы между сегментами контрольные точки.
Сегментированная линейная регрессия сегментированная регрессия, при которой отношения в интервалах получаются линейная регрессия.
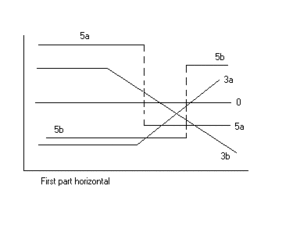
Сегментированная линейная регрессия, два сегмента
Сегментированная линейная регрессия с двумя сегментами, разделенными знаком точка останова может быть полезным для количественной оценки резкого изменения функции отклика (Yr) изменяющегося влиятельного фактора (Икс). Точку останова можно интерпретировать как критический, Безопасно, или же порог значение выше или ниже которого возникают (нежелательные) эффекты. Точка останова может быть важна при принятии решения [1]
На рисунках показаны некоторые из полученных результатов и типов регрессии.
Сегментированный регрессионный анализ основан на наличии набора ( у, х ) данные, в которых у это зависимая переменная и Икс то независимая переменная.
В наименьших квадратов метод, применяемый отдельно к каждому сегменту, с помощью которого две линии регрессии делают так, чтобы они максимально соответствовали набору данных, минимизируя сумма квадратов разностей (SSD) между наблюдаемыми (у) и рассчитанные (Yr) значения зависимой переменной, приводят к следующим двум уравнениям:
- Yr = A1.Икс + K1 за Икс
- Yr = A2.Икс + K2 за Икс > BP (точка останова)
куда:
- Yr - ожидаемое (прогнозируемое) значение у за определенную стоимость Икс;
- А1 и А2 находятся коэффициенты регрессии (с указанием наклона отрезков);
- K1 и K2 находятся константы регрессии (с указанием точки перехвата на у-ось).
Данные могут отображать множество типов или тенденций,[2] увидеть цифры.
Метод также дает два коэффициенты корреляции (Р):
- за Икс
и
- за Икс > BP (точка останова)
куда:
- это минимизированный SSD на сегмент
и
- Yа1 и Yа2 средние значения у в соответствующих сегментах.
При определении наиболее подходящей тенденции статистические тесты необходимо выполнить, чтобы убедиться, что эта тенденция является надежной (значимой).
Когда не может быть обнаружена никакая значимая точка останова, необходимо вернуться к регрессии без точки останова.
пример
На синем рисунке справа показано соотношение между урожайностью горчицы (Yr = Ym, т / га) и засоление почвы (Икс = Ss, выраженная как электрическая проводимость почвенного раствора EC в дСм / м), найдено, что:[3]
BP = 4,93, А1 = 0, К1 = 1,74, А2 = −0,129, К2 = 2,38, R12 = 0,0035 (несущественно), R22 = 0,395 (значащий) и:
- Ym = 1,74 т / га для Ss <4,93 (контрольная точка)
- Ym = −0,129 Ss + 2,38 т / га для Ss> 4,93 (контрольная точка)
это указывает на то, что засоление почвы <4,93 дСм / м является безопасным, а засоление почвы> 4,93 дСм / м снижает урожай при 0,129 т / га на единицу увеличения засоления почвы.
На рисунке также показаны доверительные интервалы и неопределенность, подробно описанные ниже.
Процедуры тестирования
Следующее статистические тесты используются для определения типа тренда:
- значимость точки останова (BP), выражая BP как функцию коэффициенты регрессии А1 и А2 а средние Y1 и Y2 из у-данные и средства X1 и X2 из Икс данных (слева и справа от БП), используя законы распространение ошибок в сложении и умножении для вычисления стандартная ошибка (SE) BP, и применяя T-тест Стьюдента
- значение A1 и А2 применяя t-распределение Стьюдента и стандартная ошибка SE of A1 и А2
- значимость разницы A1 и А2 применение t-распределения Стьюдента с использованием SE их разности.
- значимость разницы Y1 и Y2 применение t-распределения Стьюдента с использованием SE их разности.
- Более формальный статистический подход к проверке наличия точки останова - это проверка псевдо-оценки, которая не требует оценки сегментированной линии.[4].
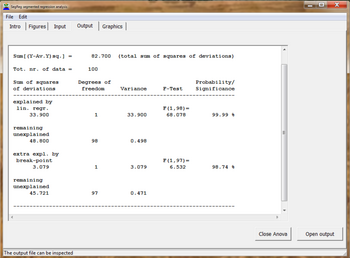
Кроме того, используется коэффициент корреляции всех данных (Ra), коэффициент детерминации или коэффициент объяснения, доверительные интервалы функций регрессии и ANOVA анализ.[5]
Коэффициент детерминации для всех данных (Cd), который должен быть максимальным в условиях, установленных тестами значимости, находится из:
где Yr - ожидаемое (прогнозируемое) значение у согласно прежним уравнениям регрессии, а Ya - среднее значение всех у значения.
Коэффициент Cd колеблется от 0 (без объяснения) до 1 (полное объяснение, идеальное совпадение).
В чистой несегментированной линейной регрессии значения Cd и Ra2 равны. В сегментированной регрессии Cd должен быть значительно больше Ra2 для обоснования сегментации.
В оптимальный значение точки останова может быть найдено таким, что коэффициент Cd равен максимум.
Диапазон отсутствия эффекта
Сегментированная регрессия часто используется для определения того, в каком диапазоне независимая переменная (X) не влияет на зависимую переменную (Y), в то время как за пределами досягаемости существует четкая реакция, будь то положительная или отрицательная. находится в начальной части домена X или, наоборот, в его последней части. Для анализа «без эффекта» применение наименьших квадратов метод сегментированного регрессионного анализа [6] может быть не самым подходящим методом, потому что цель скорее состоит в том, чтобы найти самый длинный участок, на котором отношение YX может считаться имеющим нулевой наклон, в то время как за пределами досягаемости наклон значительно отличается от нуля, но знание о наилучшем значении этого наклона не материал. Метод определения диапазона отсутствия эффекта - прогрессивная частичная регрессия. [7] по диапазону, расширяя диапазон небольшими шагами, пока коэффициент регрессии не станет значительно отличаться от нуля.
На следующем рисунке точка разрыва находится при X = 7,9, тогда как для тех же данных (см. Синий рисунок выше для урожайности горчицы) метод наименьших квадратов дает точку разрыва только при X = 4,9. Последнее значение ниже, но соответствие данных за точкой разрыва лучше. Следовательно, какой метод необходимо использовать, будет зависеть от цели анализа.
Смотрите также
- Чау-тест
- Простая регрессия
- Линейная регрессия
- Обычный метод наименьших квадратов
- Многомерные сплайны адаптивной регрессии
- Локальная регрессия
- Дизайн разрывов регрессии
- Пошаговая регрессия
- SegReg (программное обеспечение) для сегментированной регрессии
Рекомендации
- ^ Частотный и регрессионный анализ. Глава 6 в: Х.П. Ритзема (изд., 1994), Принципы и применение дренажа, Publ. 16, стр. 175-224, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. ISBN 90-70754-33-9 . Бесплатная загрузка с веб-страницы [1] , под № 20 или напрямую в формате PDF: [2]
- ^ Исследования дренажа на фермерских полях: анализ данных. Часть проекта «Жидкое золото» Международного института мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Скачать в формате PDF: [3]
- ^ Р. Дж. Остербан, Д. П. Шарма, К. Н. Сингх и К. В. Г. К. Рао, 1990, Растениеводство и засоление почвы: оценка полевых данных из Индии с помощью сегментированной линейной регрессии. В: Материалы симпозиума по осушению земель для контроля засоления в засушливых и полузасушливых регионах, 25 февраля - 2 марта 1990 г., Каир, Египет, Vol. 3, Сессия V, с. 373 - 383.
- ^ Muggeo, VMR (2016). «Тестирование с нежелательным параметром присутствует только в качестве альтернативы: подход на основе баллов с применением к сегментированному моделированию». Журнал статистических вычислений и моделирования. 86 (15): 3059–3067. Дои:10.1080/00949655.2016.1149855.
- ^ Статистическая значимость сегментированной линейной регрессии с точкой разрыва с использованием дисперсионного анализа и F-тестов. Скачать с [4] под № 13 или напрямую в формате PDF: [5]
- ^ Сегментированный регрессионный анализ, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Бесплатная загрузка с веб-страницы [6]
- ^ Частичный регрессионный анализ, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. Бесплатная загрузка с веб-страницы [7]