WikiDer > Малый додецикосододекаэдр
| Малый додецикосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 44, E = 120 V = 60 (χ = −16) |
| Лица по сторонам | 20{3}+12{5}+12{10} |
| Символ Wythoff | 3/2 5 | 5 3 5/4 | 5 |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | U33, C42, W72 |
| Двойной многогранник | Малый додекакронный гексеконтаэдр |
| Фигура вершины | 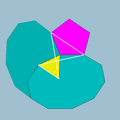 5.10.3/2.10 |
| Акроним Bowers | Саддид |
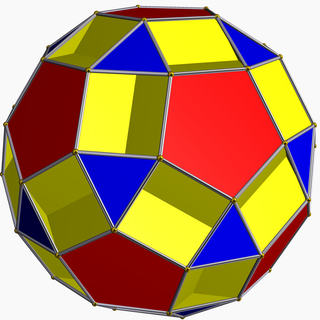
В геометрия, то малый додецикозододекаэдр (или же малый додекосидодекаэдр) это невыпуклый однородный многогранник, индексируется как U33. Имеет 44 лица (12 треугольники, 20 пятиугольники, и 12 декагоны), 120 ребер и 60 вершин.[1] Его вершина фигуры это скрещенный четырехугольник.
Связанные многогранники
Он разделяет расположение вершин с малый звездчатый усеченный додекаэдр и однородные соединения из 6 или же 12 пентаграммических призм. Он также делится своими расположение кромок с ромбикосододекаэдр (имеющий общие треугольные и пятиугольные грани), и с малый ромбидодекаэдр (имеющий общие десятиугольные грани).
 Ромбикосододекаэдр |  Малый додецикосододекаэдр |  Малый ромбидодекаэдр |
 Малый звездчатый усеченный додекаэдр |  Соединение шести пентаграммических призм |  Соединение двенадцати пентаграммических призм |
Двойной
| Малый додекакронный гексеконтаэдр | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо |  |
| Элементы | F = 60, E = 120 V = 44 (χ = −16) |
| Группа симметрии | ячас, [5,3], *532 |
| Указатель ссылок | DU33 |
| двойственный многогранник | Малый додецикосододекаэдр |
В двойственный многогранник к малому додецикосододекаэдру находится малый додекакронный гексеконтаэдр (или же малый сагиттальный дитриаконтаэдр). Визуально идентичен маленький ромбидодекакрон. Его лица - дротики. Часть каждого дротика находится внутри твердого тела и поэтому невидима в твердотельных моделях.
Пропорции
Лица имеют два угла , один из и один из . Его двугранные углы равный . Соотношение длин длинных и коротких краев составляет .
Рекомендации
- ^ Медер, Роман. "33: малый додецикосододекаэдр". MathConsult.
- Кокстер, Х. С. М. (13 мая 1954 г.). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия A, Математические и физические науки. 246 (916): 401–450. Дои:10.1098 / рста.1954.0003.
- Веннингер, Магнус (1974). Модели многогранников. Издательство Кембриджского университета. ISBN 0-521-09859-9. OCLC 1738087.
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN 978-0-521-54325-5, МИСТЕР 0730208
внешняя ссылка
- Вайсштейн, Эрик В. «Равномерный многогранник». MathWorld.
- Вайсштейн, Эрик В. «Малый додецикосододекаэдр». MathWorld.
- Вайсштейн, Эрик В. "Малый додекакронный гексеконтаэдр". MathWorld.
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |






