WikiDer > Лемма Спернерса - Википедия
В математика, Лемма Спернера это комбинаторный аналог из Теорема Брауэра о неподвижной точке, что эквивалентно ему.[1]
Лемма Спернера утверждает, что каждое Спернер окраска (описано ниже) триангуляция из п-размерный симплекс содержит ячейку, раскрашенную полным набором цветов.
Первоначальный результат такого рода был доказан Эмануэль Спернер, в связи с доказательствами неизменность домена. Раскраски Спернера использовались для эффективного вычисления фиксированные точки И в алгоритмы поиска корней, и применяются в справедливое деление (резка торта) алгоритмы. В настоящее время считается трудноразрешимой вычислительной задачей найти неподвижную точку Брауэра или, что то же самое, раскраску Спернера даже на плоскости в общем случае. Проблема в PPAD-полный, класс сложности, изобретенный Христос Пападимитриу.
Согласно советской Математическая энциклопедия (изд. Виноградов И.), родственная теорема 1929 г. Knaster, Борсук и Мазуркевич) также стали известны как Лемма Спернера - этот момент обсуждается в английском переводе (ред. М. Хазевинкель). Сейчас он широко известен как Лемма Кнастера – Куратовского – Мазуркевича..
Заявление
Одномерный случай
В одном измерении лемму Спернера можно рассматривать как дискретную версию теорема о промежуточном значении. В этом случае, по сути, говорится, что если дискретный функция принимает только значения 0 и 1, начинается со значения 0 и заканчивается значением 1, затем он должен переключать значения нечетное количество раз.
Двумерный корпус
Наиболее часто упоминается двумерный случай. Утверждается следующее:
Учитывая треугольник ABC и триангуляция Т треугольника множество S вершин Т раскрашивается тремя цветами таким образом, что
- A, B и C имеют цвета 1, 2 и 3 соответственно.
- Каждая вершина на ребре ABC должна быть окрашена только в один из двух цветов концов ее ребра. Например, каждая вершина на AC должна иметь цвет 1 или 3.
Тогда существует треугольник из Т, вершины которого раскрашены тремя разными цветами. Точнее, таких треугольников должно быть нечетное количество.
Многомерный случай
В общем случае лемма относится к п-размерный симплекс
Мы рассматриваем триангуляцию Т которое является непересекающимся делением на меньшие п-мерные симплексы. Обозначим функцию окраски как ж : S → {1,2,3,...,п,п+1}, где S снова является множеством вершин Т. Правила раскраски:
- Вершины большого симплекса раскрашены в разные цвета, т.е. е. ж(Ая) = я для 1 ≤ я ≤ п+1.
- Вершины Т расположен на любом k-мерная подповерхность большого симплекса
- раскрашены только цветами
Тогда существует нечетное количество симплексов из Т, вершины которого раскрашены всеми п + 1 цвета. В частности, должен быть хотя бы один.
Доказательство
Сначала мы обратимся к двумерному случаю. Рассмотрим график грамм построенный на основе триангуляции Т следующее:
- Вершины грамм являются членами Т плюс площадь за пределами треугольника. Две вершины соединяются ребром, если их соответствующие области имеют общую границу, причем одна конечная точка окрашена в 1, а другая - в 2.
Обратите внимание, что на интервале AB есть нечетное количество границ, окрашенных в 1-2 (просто потому, что A окрашен в 1, B окрашен в 2; и когда мы движемся по AB, должно быть нечетное количество изменений цвета, чтобы получить разные цвета в начале и в конце). Следовательно, вершина грамм соответствующая внешней области имеет нечетную степень. Но известно ( лемма о рукопожатии), что в конечном графе есть четное число вершин нечетной степени. Следовательно, оставшийся граф, исключая внешнюю область, имеет нечетное количество вершин с нечетной степенью, соответствующих членам Т.
Легко видеть, что единственно возможная степень треугольника из Т равно 0, 1 или 2, и что степень 1 соответствует треугольнику, раскрашенному тремя цветами 1, 2 и 3.
Таким образом, мы получили немного более сильный вывод, который говорит, что в триангуляции Т имеется нечетное количество (и хотя бы один) полноцветных треугольников.
Многомерный случай доказывается индукцией по размерности симплекса. Мы применяем те же рассуждения, что и в двумерном случае, чтобы заключить, что в п-мерной триангуляции существует нечетное количество полноцветных симплексов.
Комментарий
Вот разработка доказательства, данного ранее, для читателя, плохо знакомого с теория графов.
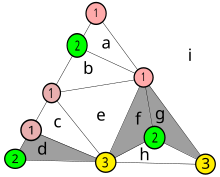
На этой диаграмме нумеруются цвета вершин приведенного ранее примера. Маленькие треугольники, все вершины которых имеют разные номера, на графике заштрихованы. Каждый маленький треугольник становится узлом в новом графе, полученном в результате триангуляции. Маленькими буквами обозначены области, восемь внутри рисунка и площадь. я обозначает пространство за его пределами.
Как описано ранее, те узлы, которые имеют общее ребро, конечные точки которого пронумерованы 1 и 2, соединяются в производном графе. Например, узел d разделяет край с внешней областью я, и все его вершины имеют разные номера, поэтому он также закрашен. Узел б не затеняется, потому что две вершины имеют одинаковые номера, но присоединяется к внешней области.
Можно добавить новый треугольник с полным номером, скажем, вставив узел с номером 3 в край между 1 и 1 узла. а, и присоединяя этот узел к другой вершине а. Для этого потребуется создать пару новых узлов, как в случае с узлами. ж и грамм.
Обобщения
Подмножества этикеток
Предположим, что каждая вершина триангуляции может быть помечена несколькими цветами, так что функция окраски ж : S → 2[n + 1].
Для каждого суб-симплекса набор разметки на его вершинах является набором-семейством над набором цветов [п+1]. Это семейство наборов можно рассматривать как гиперграф.
Если для каждой вершины v на лицевой стороне симплекса цвета в ж(v) являются подмножеством множества цветов на концах граней, то существует под-симплекс с сбалансированная маркировка - маркировка, в которой соответствующий гиперграф допускает совершенное дробное соответствие. Вот несколько примеров сбалансированной маркировки для п=2:
- ({1}, {2}, {3}) - уравновешиваются весами (1, 1, 1).
- ({1,2}, {2,3}, {3,1}) - уравновешиваются весами (1/2, 1/2, 1/2).
- ({1,2}, {2,3}, {1}) - сбалансированы по весам (0, 1, 1).
Это было доказано Шепли в 1973 г.[2] Это комбинаторный аналог Лемма KKMS.
Многогранники
Предположим, что вместо -мерный симплекс, имеем -размерный многогранник с вершины.
Тогда есть как минимум полностью маркированные симплексы, где «полностью маркированный» означает, что каждая метка на симплексе имеет свой цвет. Например, если (двумерный) многоугольник с п вершин триангулируется и раскрашивается по критерию Спернера, то имеется не менее полностью помеченные треугольники.
Общее утверждение было высказано Атанасов в 1996 году, который доказал это по делу .[3] Доказательство общего случая впервые было дано де Лоэрой, Петерсоном и Вс в 2002.[4]
Вариант радуги
Предположим, что вместо одной разметки у нас есть разные маркировки Sperner.
Мы рассматриваем пары (симплекс, перестановка) такие, что метка каждой вершины симплекса выбирается из разных разметок (так что для каждого симплекса есть разные пары).
Тогда есть как минимум полностью помеченные пары. Это было доказано Равиндра Бапат.[5]
Другой способ сформулировать эту лемму заключается в следующем. Предположим, есть люди, каждый из которых производит разные разметки Спернера для одной и той же триангуляции. Тогда существует симплекс и соответствие людей его вершинам, так что каждая вершина помечена своим владельцем по-разному (один человек маркирует свою вершину цифрой 1, другой - 2 и т. Д.). Более того, есть как минимум такие совпадения. Это можно использовать для поиска резка торта без зависти со связанными частями.
Множественные надписи
Предположим, что вместо одной разметки у нас есть разные маркировки Sperner. Потом:[6]:Thm 2.1
- Для любых положительных целых чисел чья сумма существует беби-симплекс, на котором для каждого , номер маркировки использует по крайней мере (снаружи ) различные метки. Более того, каждая метка используется как минимум одним (из ) маркировка.
- Для любых положительных целых чисел чья сумма существует беби-симплекс, на котором для каждого , наклейка используется по крайней мере (снаружи ) разные маркировки.
Обе версии сводятся к лемме Спернера, когда , или когда все маркировка идентична.
Видеть [7] для подобных обобщений.
Градусы
| Последовательность | Степень |
|---|---|
| 123 | 1 (один переключатель 1-2 и нет переключателя 2-1) |
| 12321 | 0 (один переключатель 1-2 минус один переключатель 2-1) |
| 1232 | 0 (как указано выше; последовательность отзыва циклическая) |
| 1231231 | 2 (два переключателя 1-2 и нет переключателя 2-1) |
Предположим, что треугольник триангулирован и помечен {1,2,3}. Рассмотрим циклическую последовательность меток на границе треугольника. Определить степень маркировки как разность между количеством переключателей от 1 до 2 и количеством переключателей от 2 до 1. См. примеры в таблице справа. Обратите внимание, что степень одинакова, если мы считаем переключатели от 2 до 3 минус 3 до 2 или от 3 до 1 минус 1 до 3.
Мусин доказал, что количество полностью помеченных треугольников не менее степени маркировки.[8] В частности, если степень отлична от нуля, то существует хотя бы один полностью помеченный треугольник.
Если разметка удовлетворяет условию Спернера, то ее степень равна 1: переключатели 1-2 и 2-1 находятся только на стороне между вершинами 1 и 2, а количество переключателей 1-2 должно быть на единицу больше, чем число 2–1 переключений (при переходе от вершины 1 к вершине 2). Следовательно, первоначальная лемма Шпернера следует из теоремы Мусина.
Деревья и циклы
Есть аналогичная лемма о конечном и бесконечном деревья и циклы.[9]
Кубическая лемма Шпернера
Вариант леммы Шпернера о кубе (вместо симплекса) доказал Гарольд В. Кун.[10] Это связано с Теорема Пуанкаре – Миранды.[11]
Приложения
Раскраски Спернера использовались для эффективного вычисления фиксированные точки. Раскраска Спернера может быть построена так, что полностью помеченные симплексы соответствуют неподвижным точкам данной функции. Делая триангуляцию все меньше и меньше, можно показать, что предел полностью помеченных симплексов и есть неподвижная точка. Следовательно, этот метод позволяет приблизить фиксированные точки.
По этой причине лемма Спернера также может быть использована в алгоритмы поиска корней и справедливое разделение алгоритмы; видеть Протоколы Симмонса – Су.
Лемма Спернера - одна из ключевых составляющих доказательства Теорема Монского, что квадрат нельзя разрезать на нечетное количество равновеликие треугольники.[12]
Лемму Спернера можно использовать для нахождения конкурентное равновесие в биржевое хозяйство, хотя есть более эффективные способы его найти.[13]:67
Спустя пятьдесят лет после первой публикации Спернер представил обзор развития, влияния и приложений своей комбинаторной леммы.[14]
Эквивалентные результаты
Существует несколько теорем о неподвижной точке, которые представлены в трех эквивалентных вариантах: алгебраическая топология вариант, комбинаторный вариант и вариант покрытия множества. Каждый вариант можно доказать отдельно, используя совершенно разные аргументы, но каждый вариант также можно свести к другим вариантам в своем ряду. Кроме того, каждый результат в верхней строке может быть выведен из результата под ним в том же столбце.[15]
| Алгебраическая топология | Комбинаторика | Установить покрытие |
|---|---|---|
| Теорема Брауэра о неподвижной точке | Лемма Спернера | Лемма Кнастера – Куратовского – Мазуркевича. |
| Теорема Борсука – Улама. | Лемма Такера | Теорема Люстерника – Шнирельмана. |
Смотрите также
Рекомендации
- ^ Флегг, Х. Грэм (1974). От геометрии к топологии. Лондон: Издательство английского университета. С. 84–89. ISBN 0-340-05324-0.
- ^ Шепли, Л. С. (1973-01-01), Ху, Т. С .; Робинсон, Стивен М. (ред.), «О сбалансированных играх без дополнительных выплат», Математическое программирование, Academic Press, стр. 261–290, ISBN 978-0-12-358350-5, получено 2020-06-29
- ^ Атанасов, К. Т. (1996), "О лемме Спернера", Studia Scientiarum Mathematicarum Hungarica, 32 (1–2): 71–74, МИСТЕР 1405126
- ^ Де Лоэра, Хесус А.; Петерсон, Елисей; Су, Фрэнсис Эдвард (2002), «Многогранное обобщение леммы Шпернера», Журнал комбинаторной теории, Серия А, 100 (1): 1–26, Дои:10.1006 / jcta.2002.3274, МИСТЕР 1932067
- ^ Бапат, Р. Б. (1989). «Конструктивное доказательство основанного на перестановках обобщения леммы Спернера». Математическое программирование. 44 (1–3): 113–120. Дои:10.1007 / BF01587081. S2CID 5325605.
- ^ Менье, Фредерик; Су, Фрэнсис Эдвард (2018-01-06). «Размеченные версии лемм и приложений Спернера и Фана». arXiv:1801.02044 [math.CO].
- ^ Асада, Мегуми; Фрик, Флориан; Пишароды, Вивек; Полевы, Максвелл; Стоунер, Дэвид; Цанг, Лин Хей; Веллнер, Зои (2018). "SIAM (Общество промышленной и прикладной математики)". Журнал SIAM по дискретной математике. 32: 591–610. arXiv:1701.04955. Дои:10,1137 / 17м1116210. S2CID 43932757.
- ^ Олег Р Мусин (2014). «Вокруг леммы Спернера». arXiv:1405.7513 [math.CO].
- ^ Нидермайер, Эндрю; Риццоло, Дуглас; Су, Фрэнсис Эдвард (2014), «Лемма Спернера о дереве», в Барг, Александр; Мусин, Олег Р. (ред.), Дискретная геометрия и алгебраическая комбинаторика, Современная математика, 625, Провиденс, Род-Айленд: Американское математическое общество, стр. 77–92, arXiv:0909.0339, Дои:10.1090 / conm / 625/12492, ISBN 9781470409050, МИСТЕР 3289406, S2CID 115157240
- ^ Кун, Х. В. (1960), "Некоторые комбинаторные леммы в топологии", Журнал исследований и разработок IBM, 4 (5): 518–524, Дои:10.1147 / ряд.45.0518
- ^ Майкл Мюгер (2016), Топология для работающего математика (PDF), Проект
- ^ Айгнер, Мартин; Циглер, Гюнтер М. (2010), «Один квадрат и нечетное количество треугольников», Доказательства из книги (4-е изд.), Берлин: Springer-Verlag, стр. 131–138, Дои:10.1007/978-3-642-00856-6_20, ISBN 978-3-642-00855-9
- ^ Шарф, Герберт (1967). «Суть игры N человек». Econometrica. 35 (1): 50–69. Дои:10.2307/1909383. JSTOR 1909383.
- ^ Спернер, Эмануэль (1980), «Пятьдесят лет дальнейшего развития комбинаторной леммы», Численное решение высоконелинейных задач (Симпозиумы. Алгоритмы с фиксированной точкой и проблемы дополнительности, Саутгемптонский университет, 1979), Северная Голландия, Амстердам-Нью-Йорк, стр. 183–197, 199–217, МИСТЕР 0559121
- ^ Nyman, Kathryn L .; Су, Фрэнсис Эдвард (2013), «Эквивалент Борсука – Улама, из которого непосредственно следует лемма Спернера», Американский математический ежемесячный журнал, 120 (4): 346–354, Дои:10.4169 / amer.math.monthly.120.04.346, МИСТЕР 3035127
внешняя ссылка
- Доказательство леммы Спернера. в завязать узел
- Лемма Спернера и игра треугольников, на сайте n-rich.