WikiDer > Подигра идеальное равновесие

Subgame perfect equilibrium
Подигра Идеальное равновесие
А концепция решения в теория игры
Отношение
Подмножестворавновесие по Нэшу
Пересекается сЭволюционно устойчивая стратегия
Значимость
ПредложеноРайнхард Зельтен
Используется дляИгры с расширенной формой
ПримерУльтиматум игра

В теория игры, а подигра идеальное равновесие (или же подигра идеальное равновесие по Нэшу) это уточнение из равновесие по Нэшу используется в динамические игры. А профиль стратегии является совершенным равновесием для подыгры, если оно представляет собой равновесие по Нэшу каждого вспомогательная игра оригинальной игры. Неформально это означает, что в любой момент игры поведение игроков, начиная с этого момента, должно представлять собой равновесие по Нэшу для продолжения игры (т. Е. Вспомогательной игры), независимо от того, что произошло раньше. Каждый конечная обширная игра с идеальным отзывом имеет идеальное равновесие подигры.[1]

Общий метод определения идеального равновесия для подыгры в случае конечной игры: обратная индукция. Здесь сначала рассматриваются последние действия в игре и определяются действия, которые должен предпринять последний игрок в каждой возможной ситуации, чтобы максимизировать его / ее. полезность. Затем предполагается, что эти действия будет выполнять последний актор, и учитываются предпоследние действия, снова выбирая те, которые максимизируют полезность этого актора. Этот процесс продолжается до тех пор, пока не будет сделан первый ход игры. Остающиеся стратегии - это совокупность совершенных равновесий всех подигр для обширных игр с совершенной информацией с конечным горизонтом.[1] Однако обратная индукция не может применяться к играм несовершенный или же неполная информация потому что это влечет за собой сокращение не синглетонов информационные наборы.

Совершенное равновесие в подыгре обязательно удовлетворяет принцип однократного отклонения.

Множество совершенных равновесий для подыгры для данной игры всегда является подмножеством множества равновесий Нэша для этой игры. В некоторых случаях наборы могут быть идентичными.

В ультиматумная игра представляет собой интуитивно понятный пример игры с меньшим количеством совершенных равновесий подигр, чем равновесий Нэша.

Пример

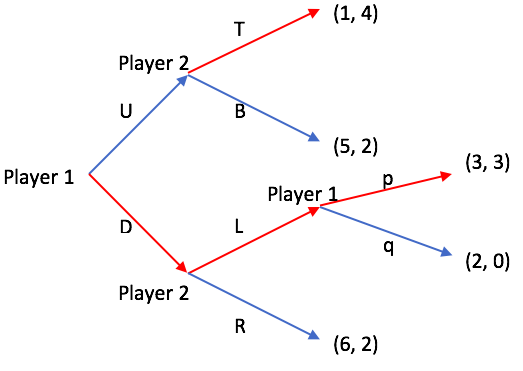
Определение идеального равновесия во вспомогательной игре с использованием обратной индукции показано ниже на рисунке 1. Стратегии для Игрока 1 задаются как {Up, Uq, Dp, Dq}, тогда как у Игрока 2 есть следующие стратегии: {TL, TR, BL, BR}. В этом примере есть 4 подигры с 3 собственными подиграми.

Рисунок 1

Используя обратную индукцию, игроки будут выполнять следующие действия для каждой вспомогательной игры:

  • Подигра для действий p и q: Игрок 1 выполнит действие p с выигрышем (3, 3), чтобы максимизировать выигрыш Игрока 1, поэтому выигрыш за действие L станет (3,3).
  • Подигра для действий L и R: Игрок 2 выполнит действие L для 3> 2, поэтому выигрыш за действие D станет (3, 3).
  • Подигра для действий T и B: Игрок 2 выполнит действие T, чтобы максимизировать выигрыш Игрока 2, поэтому выигрыш за действие U станет (1, 4).
  • Подигра для действий U и D: Игрок 1 выполнит действие D, чтобы максимизировать выигрыш Игрока 1.

Таким образом, совершенное равновесие в подигре - это {Dp, TL} с выигрышем (3, 3).

Игра в расширенной форме с неполной информацией представлена ​​ниже на рисунке 2. Обратите внимание, что узел для Игрока 1 с действиями A и B и всеми последующими действиями является вспомогательной игрой. Узлы игрока 2 не являются вспомогательной игрой, поскольку они являются частью того же набора информации.

фигура 2

Первая игра в нормальной форме - это представление в нормальной форме всей игры в развернутой форме. На основании предоставленной информации (UA, X), (DA, Y) и (DB, Y) - все это равновесия Нэша для всей игры.

Вторая игра в нормальной форме - это представление в нормальной форме подигры, начиная со второго узла Игрока 1 с действиями A и B. Для второй игры в нормальной форме равновесие по Нэшу во вспомогательной игре равно (A, X).

Для всей игры равновесия по Нэшу (DA, Y) и (DB, Y) не являются идеальными уравнениями для подыгры, поскольку ход игрока 2 не составляет равновесия по Нэшу. Равновесие по Нэшу (UA, X) является совершенным по подыгре, потому что оно включает в себя равновесие по Нэшу (A, X) как часть своей стратегии.[2]

Чтобы решить эту игру, сначала найдите равновесие Нэша путем взаимного наилучшего отклика подигры 1. Затем используйте обратную индукцию и вставьте (A, X) → (3,4) так, чтобы (3,4) стали выигрышами для подигры 2.[2]

Пунктирная линия показывает, что игрок 2 не знает, сыграет ли игрок 1 A или B в одновременной игре.

Подигра 1 решена, и (3,4) заменяет всю Подигру 1, и игрок 1 выберет U -> (3,4) Решение для Подигры 1

Игрок 1 выбирает U, а не D, потому что 3> 2 для выигрыша Игрока 1. В результате получается равновесие (A, X) → (3,4).

Решение идеального равновесия в подигре

Таким образом, совершенное равновесие в подигре посредством обратной индукции - это (UA, X) с выигрышем (3, 4).

В конечно повторяющихся играх

Для игр с конечным числом повторений, если в поэтапной игре есть только одно уникальное равновесие по Нэшу, идеальное равновесие во вспомогательной игре состоит в том, чтобы играть без учета прошлых действий, рассматривая текущую вспомогательную игру как игру с одним выстрелом. Примером этого является конечно повторяющееся Дилемма заключенного игра. Используя обратную индукцию, последняя подигра в конечно-повторяющейся дилемме Заключенного требует, чтобы игроки играли в уникальное равновесие Нэша (оба игрока дезертируют). Из-за этого во всех играх, предшествующих последней вспомогательной игре, также будет играть равновесие по Нэшу, чтобы максимизировать свои однопериодные выплаты.

Если сценическая игра в конечно повторяющейся игре имеет несколько равновесий по Нэшу, можно построить совершенные равновесия подигры для выполнения действий равновесия по Нэшу вне сценической игры посредством структуры «кнута и пряника». Один игрок может использовать равновесие по Нэшу в рамках одной поэтапной игры, чтобы стимулировать игру не по равновесию по Нэшу, в то же время используя равновесие по Нэшу в поэтапной игре с меньшим выигрышем для другого игрока, если он решит отказаться.[3]

Нахождение идеального равновесия по подиграм

Одна игра, в которой решение обратной индукции хорошо известно, это крестики-нолики

Райнхард Зельтен доказал, что любая игра, которую можно разбить на «подигры», содержащие подмножество всех доступных вариантов в основной игре, будет иметь идеальную стратегию равновесия по Нэшу (возможно, как смешанная стратегия дающие недетерминированные подигровые решения). Совершенство подигр используется только с играми полная информация. Совершенство подигры можно использовать с обширная форма игры полного но несовершенная информация.

Совершенное по подиграм равновесие по Нэшу обычно выводится следующим образом:обратная индукция"от различных конечных результатов игры, устраняя ветви, которые потребовали бы от любого игрока сделать ход, который не заслуживает доверия (потому что это не оптимально) из этого узел. Одна игра, в которой решение обратной индукции хорошо известно, это крестики-нолики, но теоретически даже Идти имеет такую ​​оптимальную стратегию для всех игроков. Проблема взаимосвязи между совершенством подыгры и обратной индукцией была решена Камински (2019), который доказал, что обобщенная процедура обратной индукции приводит к идеальным равновесиям во всех подиграх в играх, которые могут иметь бесконечную длину, бесконечные действия в качестве каждого набора информации и несовершенные информация, если выполнено условие окончательной поддержки.

Интересный аспект слова «заслуживающий доверия» в предыдущем абзаце состоит в том, что в целом (без учета необратимости достижения под-игр) существуют стратегии, которые превосходят идеальные стратегии под-игры, но которые не заслуживают доверия в том смысле, что угроза их выполнение нанесет вред игроку, создающему угрозу, и предотвратит эту комбинацию стратегий. Например, в игре "курица«если у одного игрока есть возможность вырвать руль из своей машины, он всегда должен использовать его, потому что это приводит к« вспомогательной игре », в которой их рациональный противник не может сделать то же самое (и убить их обоих). -ripper всегда побеждает в игре (заставляя своего противника уклоняться), и угроза противника самоубийственно последовать его примеру не заслуживает доверия.

Смотрите также

Рекомендации

  1. ^ а б Осборн, М. Дж. (2004). Введение в теорию игр. Издательство Оксфордского университета.
  2. ^ а б Джоэл., Ватсон (09.05.2013). Стратегия: введение в теорию игр (Третье изд.). Нью-Йорк. ISBN 9780393918380. OCLC 842323069.
  3. ^ Такако, Фудзивара-Греве. Некооперативная теория игр. Токио. ISBN 9784431556442. OCLC 911616270.

внешняя ссылка