WikiDer > Поперечная волна
эта статья нужны дополнительные цитаты для проверка. (Май 2019) (Узнайте, как и когда удалить этот шаблон сообщения) |
В физика, а поперечная волна это волна который колеблется перпендикулярно направлению волны или пути распространения.
Простой пример - волны, которые можно создать на горизонтальной длине струны, закрепив один конец и перемещая другой конец вверх и вниз.
Другой пример - волны, которые создаются на мембране барабан. Волны распространяются в направлениях, параллельных плоскости мембраны, но сама мембрана смещается вверх и вниз, перпендикулярно этой плоскости.
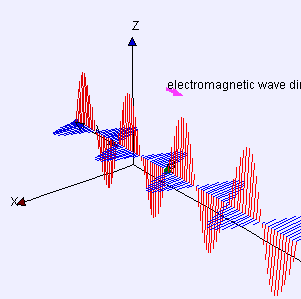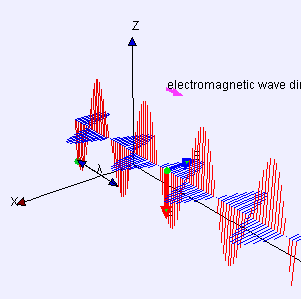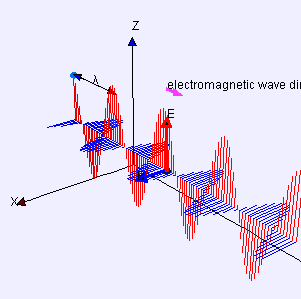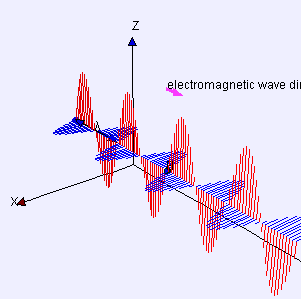
Свет еще один пример поперечной волны, где колебания электрический и магнитные поля, которые направлены под прямым углом к идеальным световым лучам, описывающим направление распространения.
Поперечные волны обычно возникают в эластичный твердые вещества; колебания в этом случае представляют собой смещение твердых частиц от их релаксированного положения в направлениях, перпендикулярных распространению волны. Поскольку эти смещения соответствуют локальному деформация сдвига материала поперечная волна такой природы называется поперечная волна. В сейсмология, поперечные волны также называют вторичные волны или S-волны.
Поперечные волны контрастируют с продольные волны, где колебания происходят в направлении волны. Стандартный пример продольной волны - это звуковая волна или «волна давления» в газах, жидкостях или твердых телах, колебания которых вызывают сжатие и расширение материала, через который распространяется волна. Волны давления в геофизике называют «первичными волнами» или «P-волнами».
Математическая формулировка
Математически простейший вид поперечной волны - это плоская линейно поляризованная синусоидальная один. «Плоскость» здесь означает, что направление распространения неизменно и одинаково по всей среде; "линейно поляризованный"означает, что направление смещения также неизменно и одинаково для всей среды; а величина смещения равна синусоидальный функция только времени и положения вдоль направления распространения.
Движение такой волны можно математически выразить следующим образом. Позволять d быть направлением распространения (a вектор с единичной длиной), и о любой ориентир в среде. Позволять ты направление колебаний (другой вектор единичной длины, перпендикулярный d). Смещение частицы в любой точке п среды и в любое время т (секунды) будет
где А волна амплитуда или прочность, Т это его период, v это скорость распространения, и φ это его фаза в о. Все эти параметры действительные числа. Символ «•» обозначает внутренний продукт двух векторов.
По этому уравнению волна распространяется в направлении d и колебания происходят вперед и назад по направлению ты. Волна называется линейно поляризованной в направлении ты.
Наблюдатель, который смотрит в фиксированную точку п увидит, как частица там движется простым гармонический (синусоидальное) движение с периодом Т секунды, с максимальным смещением частиц А во всех смыслах; то есть с частота из ж = 1/Т полные циклы колебаний каждую секунду. Снимок всех частиц в фиксированное время т покажет одинаковое смещение для всех частиц на каждой плоскости, перпендикулярной к d, причем смещения в последовательных плоскостях образуют синусоидальную структуру, причем каждый полный цикл продолжается вдоль d посредством длина волны λ = v Т = v/ж. Весь узор движется в направлении d со скоростью V.
Это же уравнение описывает плоскую линейно поляризованную синусоидальную световую волну, за исключением того, что «смещение» S(п, т) - электрическое поле в точке п и время т. (Магнитное поле будет описываться тем же уравнением, но с направлением «смещения», перпендикулярным обоим d и ты, и другую амплитуду.)
Принцип суперпозиции
В однородный эластичная средасложные колебания (колебания материала или световых потоков) можно описать как суперпозиция многих простых синусоидальных волн, поперечных (линейно поляризованных) или продольных.
Например, колебания струны скрипки можно проанализировать как сумму множества поперечных волн разной частоты, которые смещают струну вверх, вниз или слева направо. Рябь в пруду можно рассматривать как комбинацию поперечных и продольных волн (гравитационные волны), которые распространяются вместе.
Круговая поляризация
Если среда линейная и допускает несколько независимых направлений перемещения для одного и того же направления движения d, мы можем выбрать два взаимно перпендикулярных направления поляризации и выразить любую волну, линейно поляризованную в любом другом направлении, как линейную комбинацию (смешение) этих двух волн.
Комбинируя две волны с одинаковой частотой, скоростью и направлением движения, но с разными фазами и независимыми направлениями смещения, можно получить по кругу или эллиптически поляризованный волна. В такой волне частицы описывают круговые или эллиптические траектории, а не движутся вперед и назад.
Для понимания может оказаться полезным вернуться к мысленному эксперименту с натянутой веревкой, упомянутой выше. Обратите внимание, что вы также можете запускать волны на струне, перемещая руку вправо и влево, а не вверх и вниз. Это важный момент. Волны могут двигаться в двух независимых (ортогональных) направлениях (это верно для любых двух направлений под прямым углом, для ясности выбраны вверх и вниз, вправо и влево). Любые волны, создаваемые движением руки по прямой линии. являются линейно поляризованными волнами.
Но теперь представьте, что двигаете рукой по кругу. Ваше движение вызовет спиральную волну на струне. Вы двигаете рукой одновременно вверх и вниз и из стороны в сторону. Максимумы движения из стороны в сторону происходят на четверти длины волны (или четверти пути по окружности, то есть 90 градусов или π / 2 радиан) от максимумов движения вверх и вниз. В любой точке струны смещение струны будет описывать тот же круг, что и ваша рука, но с задержкой из-за скорости распространения волны. Обратите также внимание на то, что вы можете двигать рукой по кругу по часовой стрелке или по кругу против часовой стрелки. Эти чередующиеся круговые движения создают волны с правой и левой круговой поляризацией.
Если ваш круг несовершенен, регулярное движение будет описывать эллипс и производить волны с эллиптической поляризацией. В крайнем случае эксцентриситет ваш эллипс станет прямой линией, производящей линейную поляризацию вдоль главной оси эллипса. Эллиптическое движение всегда можно разложить на два ортогональных линейных движения с неравной амплитудой и сдвигом по фазе на 90 градусов, при этом круговая поляризация является частным случаем, когда два линейных движения имеют одинаковую амплитуду.
Смотрите также
- Продольная волна
- Светоносный эфир - постулируемая среда для световых волн; принятие того, что свет был поперечной волной, побудило поиск свидетельств этой физической среды
- Расщепление поперечной волны
- Синусоидальные плоские волновые решения уравнения электромагнитной волны
- Поперечный режим
- Эластография
- Визуализация упругости сдвиговой волны