WikiDer > Тутте 12 клеток
| Тутте 12 клеток | |
|---|---|
 Тутте 12 клеток | |
| Названный в честь | В. Т. Тутте |
| Вершины | 126 |
| Края | 189 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 12 |
| Автоморфизмы | 12096 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Характеристики | Кубический Клетка Гамильтониан Полусимметричный Двудольный |
| Таблица графиков и параметров | |
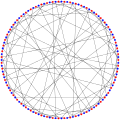
в математический поле теория графов, то Тутте 12 клеток или же Граф Бенсона[1] это 3-регулярный граф со 126 вершинами и 189 ребрами, названными в честь В. Т. Тутте.[2]
Tutte 12-клетка уникальна (3-12) -клетка (последовательность A052453 в OEIS). Он был открыт К. Т. Бенсоном в 1966 году.[3] Она имеет хроматическое число 2 (двудольный), хроматический индекс 3, обхват 12 (как 12-клетка) и диаметр 6. Его номер перехода равен 170 и считается наименьшим кубическим графом с этим числом пересечений.[4][5]
Строительство
Tutte с 12 клетками - это кубический Гамильтонов граф и может быть определена Обозначение LCF [17, 27, –13, –59, –35, 35, –11, 13, –53, 53, –27, 21, 57, 11, –21, –57, 59, –17]7.[6]
Имеется с точностью до изоморфизма ровно два обобщенные шестиугольники порядка (2,2) что доказано Коэном и Титсом. Это разделенный шестиугольник Кэли H (2) и его дуальная точка. Ясно, что оба они имеют один и тот же граф инцидентности, который фактически изоморфен 12-клетке Тутте.[1]
В Балабан 11-клеточный может быть сконструирован путем вырезания из 12-клетки Тутте путем удаления небольшого поддерева и подавления результирующих вершин второй степени.[7]
Алгебраические свойства
Группа автоморфизмов 12-клетки Тутте имеет порядок 12 096 и является полупрямой продукт из проективная специальная унитарная группа БП (3,3) с циклическая группа Z/2Z.[1] Он действует транзитивно на своих ребрах, но не на вершинах, что делает его полусимметричный граф, регулярный граф, реберно-транзитивный но нет вершинно-транзитивный. Фактически, группа автоморфизмов 12-клетки Тутте сохраняет двудольные части и действует примитивно на каждой части. Такие графы называются би-примитивными графами, и существует только пять кубических би-примитивных графов; они называются графами Иофиновой-Иванова и имеют порядок 110, 126, 182, 506 и 990.[8]
Все кубические полусимметричные графы, содержащие до 768 вершин, известны. В соответствии с Кондер, Малнич, Марушич и Поточник, 12-клетка Тутте - это уникальный кубический полусимметричный граф на 126 вершинах и пятый по размеру кубический полусимметричный граф после Серый график, то Граф Иофиновой – Иванова на 110 вершинах, то Любляна график и граф на 120 вершин с обхватом 8.[9]
В характеристический многочлен Тутте 12-клетка - это
Это единственный граф с таким характеристическим многочленом; следовательно, 12-клетка определяется ее спектр.
Галерея
В хроматическое число Тутте 12-клетка - 2.
В хроматический индекс Тутте с 12 клетками - 3.
Рекомендации
- ^ а б c Джеффри Эксу и Роберт Джейчай, Динамическое обследование клеток, Электр. J. Combin. 15 (2008).
- ^ Вайсштейн, Эрик В. "Тутте 12-клетка". MathWorld.
- ^ Бенсон, К. Т. «Минимальные регулярные графы обхвата 8 и 12». Может. J. Math. 18, 1091–1094, 1966.
- ^ Эксу, Дж. «Прямолинейные рисунки знаменитых графов».
- ^ Пегг, Э. Т. и Эксу, Г. «Графики пересекающихся чисел». Mathematica J. 11, 2009.
- ^ Польстер Б. Геометрическая иллюстрированная книга. Нью-Йорк: Springer, стр. 179, 1998.
- ^ Балабан, А. Т. «Трехвалентные графики девятого и одиннадцатого обхватов и отношения между клетками». Преподобный Roumaine Math 18, 1033–1043, 1973.
- ^ Иофинова М.Е., Иванов А.А. Биопримитивные кубические графы. Исследования по алгебраической теории комбинаторных объектов. С. 123–134, 2002. (Всесоюз. Научно-исслед. ИСистем. Исслед., Москва, 1985. С. 137–152).
- ^ Кондер, Марстон; Малнич, Александр; Марушич, Драган; Поточник, Примож (2006), "Перепись полусимметричных кубических графов с числом вершин до 768", Журнал алгебраической комбинаторики, 23: 255–294, Дои:10.1007 / s10801-006-7397-3.