WikiDer > Равномерный 9-многогранник

Uniform 9-polytope

Графики трех обычный и связанные однородные многогранники

9-симплекс						Ректифицированный 9-симплексный
Усеченный 9-симплексный						Сквозной 9-симплексный
Ранцинатный 9-симплексный						Стерилизованный 9-симплекс
Пятисторонний 9-симплекс						Hexicated 9-симплекс
Семеричный 9-симплексный						Октеллированный 9-симплексный
9-ортоплекс						9-куб
Усеченный 9-ортоплекс						Усеченный 9-куб
Ректифицированный 9-ортоплекс						Ректифицированный 9-куб
9-полукруглый						Усеченный 9-полукуб

В девятимерном геометрия, а девятимерный многогранник или же 9-многогранник это многогранник содержится в фасетках 8-многогранников. Каждый 7-многогранник гребень разделяют ровно два 8-многогранник грани.

А равномерный 9-многогранник тот, который вершинно-транзитивный, и построен из равномерный 8-многогранник грани.

Правильные 9-многогранники

Правильные 9-многогранники можно представить в виде Символ Шлефли {p, q, r, s, t, u, v, w}, причем ш {p, q, r, s, t, u, v} 8-многогранник грани вокруг каждого вершина горы.

Таких ровно три выпуклые правильные 9-многогранники:

{3,3,3,3,3,3,3,3} - 9-симплекс
{4,3,3,3,3,3,3,3} - 9-куб
{3,3,3,3,3,3,3,4} - 9-ортоплекс

Не существует невыпуклых правильных 9-многогранников.

Эйлерова характеристика

Топология любого данного 9-многогранника определяется его Бетти числа и коэффициенты кручения.^[1]

Ценность Эйлерова характеристика Используется для характеристики многогранников, бесполезно обобщается на более высокие измерения, независимо от их базовой топологии. Эта неадекватность характеристики Эйлера для надежного различения различных топологий в более высоких измерениях привела к открытию более сложных чисел Бетти.^[1]

Точно так же понятие ориентируемости многогранника недостаточно для характеристики скручивания поверхности тороидальных многогранников, и это привело к использованию коэффициентов кручения.^[1]

Равномерные 9-многогранники фундаментальными группами Кокстера

Равномерные 9-многогранники с отражательной симметрией могут быть порождены этими тремя группами Кокстера, представленными перестановками колец Диаграммы Кокстера-Дынкина:

Группа Кокстера		Диаграмма Кокстера-Дынкина
А₉	[3⁸]
B₉	[4,3⁷]
D₉	[3^6,1,1]

Выбранные регулярные и равномерные 9-многогранники из каждого семейства включают:

Симплекс семья: A₉ [3⁸] -
- 271 равномерный 9-многогранник как перестановка колец в групповой диаграмме, включая один регулярный:
  1. {3⁸} - 9-симплекс или же дека-9-топ или же гнилой хлопок -
Гиперкуб/ортоплекс семья: B₉ [4,3⁸] -
- 511 равномерных 9-многогранников как перестановок колец в групповой диаграмме, в том числе два регулярных:
  1. {4,3⁷} - 9-куб или же вовлекать -
  2. {3⁷,4} - 9-ортоплекс или же Enneacross -
Демигиперкуб D₉ семья: [3^6,1,1] -
- 383 равномерных 9-многогранников как перестановок колец в групповой диаграмме, в том числе:
  1. {3^1,6,1} - 9-полукруглый или же демиеннерракт, 1₆₁ - ; также как h {4,3⁸} .
  2. {3^6,1,1} - 9-ортоплекс, 6₁₁ -

А₉ семья

А₉ семейство имеет симметрию порядка 3628800 (10 факториалов).

Существует 256 + 16-1 = 271 форма, основанная на всех перестановках Диаграммы Кокстера-Дынкина с одним или несколькими кольцами. Все они перечислены ниже. Названия акронимов в стиле Bowers приведены в скобках для перекрестных ссылок.

#	График	Диаграмма Кокстера-Дынкина Символ Шлефли Имя	Количество элементов
#	График	Диаграмма Кокстера-Дынкина Символ Шлефли Имя	8 лиц	7 лиц	6 лиц	5 лиц	4 лица	Клетки	Лица	Края	Вершины
1		т₀{3,3,3,3,3,3,3,3} 9-симплекс (день)	10	45	120	210	252	210	120	45	10
2		т₁{3,3,3,3,3,3,3,3} Ректифицированный 9-симплексный (reday)								360	45
3		т₂{3,3,3,3,3,3,3,3} Биректифицированный 9-симплекс (breday)								1260	120
4		т₃{3,3,3,3,3,3,3,3} Триректифицированный 9-симплексный (вторник)								2520	210
5		т₄{3,3,3,3,3,3,3,3} Квадриректифицированный 9-симплексный (icoy)								3150	252
6		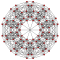т_0,1{3,3,3,3,3,3,3,3} Усеченный 9-симплексный (вторник)								405	90
7		т_0,2{3,3,3,3,3,3,3,3} Сквозной 9-симплексный								2880	360
8		т_1,2{3,3,3,3,3,3,3,3} Bitruncated 9-симплекс								1620	360
9		т_0,3{3,3,3,3,3,3,3,3} Ранцинатный 9-симплексный								8820	840
10		т_1,3{3,3,3,3,3,3,3,3} Бикантеллированный 9-симплекс								10080	1260
11		т_2,3{3,3,3,3,3,3,3,3} Усеченный 9-симплекс (вторник)								3780	840
12		т_0,4{3,3,3,3,3,3,3,3} Стерилизованный 9-симплекс								15120	1260
13		т_1,4{3,3,3,3,3,3,3,3} Бирунцинированный 9-симплекс								26460	2520
14		т_2,4{3,3,3,3,3,3,3,3} Треугольник 9-симплекс								20160	2520
15		т_3,4{3,3,3,3,3,3,3,3} Квадроусеченный 9-симплексный								5670	1260
16		т_0,5{3,3,3,3,3,3,3,3} Пятисторонний 9-симплекс								15750	1260
17		т_1,5{3,3,3,3,3,3,3,3} Бистерифицированный 9-симплексный								37800	3150
18		т_2,5{3,3,3,3,3,3,3,3} Усеченный 9-симплекс								44100	4200
19		т_3,5{3,3,3,3,3,3,3,3} Четырехсторонний 9-симплексный								25200	3150
20		т_0,6{3,3,3,3,3,3,3,3} Hexicated 9-симплекс								10080	840
21		т_1,6{3,3,3,3,3,3,3,3} Двузубчатый 9-симплексный								31500	2520
22		т_2,6{3,3,3,3,3,3,3,3} Тристерифицированный 9-симплекс								50400	4200
23		т_0,7{3,3,3,3,3,3,3,3} Семеричный 9-симплексный								3780	360
24		т_1,7{3,3,3,3,3,3,3,3} Бигексикатед 9-симплекс								15120	1260
25		т_0,8{3,3,3,3,3,3,3,3} Октеллированный 9-симплексный								720	90
26		т_0,1,2{3,3,3,3,3,3,3,3} Cantitruncated 9-симплекс								3240	720
27		т_0,1,3{3,3,3,3,3,3,3,3} Runcitruncated 9-симплекс								18900	2520
28		т_0,2,3{3,3,3,3,3,3,3,3} Runcicantellated 9-симплекс								12600	2520
29		т_1,2,3{3,3,3,3,3,3,3,3} Бикантитроусеченный 9-симплекс								11340	2520
30		т_0,1,4{3,3,3,3,3,3,3,3} Стеритоусеченный 9-симплекс								47880	5040
31		т_0,2,4{3,3,3,3,3,3,3,3} Стерикантеллированный 9-симплекс								60480	7560
32		т_1,2,4{3,3,3,3,3,3,3,3} Biruncitruncated 9-симплекс								52920	7560
33		т_0,3,4{3,3,3,3,3,3,3,3} Стерирунированный 9-симплекс								27720	5040
34		т_1,3,4{3,3,3,3,3,3,3,3} Biruncicantellated 9-симплекс								41580	7560
35		т_2,3,4{3,3,3,3,3,3,3,3} Трикантитусеченный 9-симплекс								22680	5040
36		т_0,1,5{3,3,3,3,3,3,3,3} Пятиусеченный 9-симплекс								66150	6300
37		т_0,2,5{3,3,3,3,3,3,3,3} Пятиугольник 9-симплекс								126000	12600
38		т_1,2,5{3,3,3,3,3,3,3,3} Бистеритусеченный 9-симплекс								107100	12600
39		т_0,3,5{3,3,3,3,3,3,3,3} Pentiruncinated 9-симплекс								107100	12600
40		т_1,3,5{3,3,3,3,3,3,3,3} Бистерикантеллированный 9-симплекс								151200	18900
41		т_2,3,5{3,3,3,3,3,3,3,3} Усеченный 9-симплекс								81900	12600
42		т_0,4,5{3,3,3,3,3,3,3,3} Пентистерифицированный 9-симплексный								37800	6300
43		т_1,4,5{3,3,3,3,3,3,3,3} Бистеринцинированный 9-симплекс								81900	12600
44		т_2,4,5{3,3,3,3,3,3,3,3} Трирунцианателлитный 9-симплексный								75600	12600
45		т_3,4,5{3,3,3,3,3,3,3,3} Квадрикантоусеченный 9-симплексный								28350	6300
46		т_0,1,6{3,3,3,3,3,3,3,3} Hexitruncated 9-симплекс								52920	5040
47		т_0,2,6{3,3,3,3,3,3,3,3} Гексикантеллированный 9-симплекс								138600	12600
48		т_1,2,6{3,3,3,3,3,3,3,3} Двузубчатоусеченный 9-симплекс								113400	12600
49		т_0,3,6{3,3,3,3,3,3,3,3} Гексирунированный 9-симплекс								176400	16800
50		т_1,3,6{3,3,3,3,3,3,3,3} Бипентикантеллитный 9-симплексный								239400	25200
51		т_2,3,6{3,3,3,3,3,3,3,3} Тристеритусеченный 9-симплекс								126000	16800
52		т_0,4,6{3,3,3,3,3,3,3,3} Гексистерифицированный 9-симплекс								113400	12600
53		т_1,4,6{3,3,3,3,3,3,3,3} Бипентирунцинированный 9-симплекс								226800	25200
54		т_2,4,6{3,3,3,3,3,3,3,3} Тристерикантеллированный 9-симплекс								201600	25200
55		т_0,5,6{3,3,3,3,3,3,3,3} Шестиугольник 9-симплекс								32760	5040
56		т_1,5,6{3,3,3,3,3,3,3,3} Бипентистерифицированный 9-симплексный								94500	12600
57		т_0,1,7{3,3,3,3,3,3,3,3} Гептоусеченный 9-симплекс								23940	2520
58		т_0,2,7{3,3,3,3,3,3,3,3} Гептикантеллированный 9-симплексный								83160	7560
59		т_1,2,7{3,3,3,3,3,3,3,3} Бигекситусеченный 9-симплекс								64260	7560
60		т_0,3,7{3,3,3,3,3,3,3,3} Гептирунцинированный 9-симплекс								144900	12600
61		т_1,3,7{3,3,3,3,3,3,3,3} Бигексикантеллированный 9-симплекс								189000	18900
62		т_0,4,7{3,3,3,3,3,3,3,3} Гептистерифицированный 9-симплексный								138600	12600
63		т_1,4,7{3,3,3,3,3,3,3,3} Бигексирунированный 9-симплекс								264600	25200
64		т_0,5,7{3,3,3,3,3,3,3,3} Гептипентельчатый 9-симплексный								71820	7560
65		т_0,6,7{3,3,3,3,3,3,3,3} Гепихоксикат 9-симплекс								17640	2520
66		т_0,1,8{3,3,3,3,3,3,3,3} Octitruncated 9-симплекс								5400	720
67		т_0,2,8{3,3,3,3,3,3,3,3} Октикантеллированный 9-симплекс								25200	2520
68		т_0,3,8{3,3,3,3,3,3,3,3} Октирунцинированный 9-симплекс								57960	5040
69		т_0,4,8{3,3,3,3,3,3,3,3} Октистерифицированный 9-симплексный								75600	6300
70		т_0,1,2,3{3,3,3,3,3,3,3,3} Runcicantitruncated 9-симплекс								22680	5040
71		т_0,1,2,4{3,3,3,3,3,3,3,3} Стериканитусеченный 9-симплекс								105840	15120
72		т_0,1,3,4{3,3,3,3,3,3,3,3} Стерино-усеченный 9-симплексный								75600	15120
73		т_0,2,3,4{3,3,3,3,3,3,3,3} Стерируксантеллированный 9-симплексный								75600	15120
74		т_1,2,3,4{3,3,3,3,3,3,3,3} Biruncicantitruncated 9-симплекс								68040	15120
75		т_0,1,2,5{3,3,3,3,3,3,3,3} Penticantitruncated 9-симплекс								214200	25200
76		т_0,1,3,5{3,3,3,3,3,3,3,3} Pentiruncitruncated 9-симплекс								283500	37800
77		т_0,2,3,5{3,3,3,3,3,3,3,3} Пятизубчатый 9-симплексный								264600	37800
78		т_1,2,3,5{3,3,3,3,3,3,3,3} Бистерикантоусеченный 9-симплекс								245700	37800
79		т_0,1,4,5{3,3,3,3,3,3,3,3} Пентистеритусеченный 9-симплекс								138600	25200
80		т_0,2,4,5{3,3,3,3,3,3,3,3} Пентистерический 9-симплексный								226800	37800
81		т_1,2,4,5{3,3,3,3,3,3,3,3} Бистерин-усеченный 9-симплексный								189000	37800
82		т_0,3,4,5{3,3,3,3,3,3,3,3} Пентистерирунцинированный 9-симплекс								138600	25200
83		т_1,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantellated 9-симплекс								207900	37800
84		т_2,3,4,5{3,3,3,3,3,3,3,3} Усеченный 9-симплексный								113400	25200
85		т_0,1,2,6{3,3,3,3,3,3,3,3} Гексикант усеченный 9-симплекс								226800	25200
86		т_0,1,3,6{3,3,3,3,3,3,3,3} Гексирунциркулированный 9-симплекс								453600	50400
87		т_0,2,3,6{3,3,3,3,3,3,3,3} Шестигранникантеллированный 9-симплексный								403200	50400
88		т_1,2,3,6{3,3,3,3,3,3,3,3} Бипентикантитусеченный 9-симплекс								378000	50400
89		т_0,1,4,6{3,3,3,3,3,3,3,3} Гексистерия усеченная 9-симплексная								403200	50400
90		т_0,2,4,6{3,3,3,3,3,3,3,3} Гексистерический 9-симплексный								604800	75600
91		т_1,2,4,6{3,3,3,3,3,3,3,3} Бипентирунцирующий усеченный 9-симплекс								529200	75600
92		т_0,3,4,6{3,3,3,3,3,3,3,3} Гексистеринцинированный 9-симплекс								352800	50400
93		т_1,3,4,6{3,3,3,3,3,3,3,3} Двустворчатый 9-симплексный								529200	75600
94		т_2,3,4,6{3,3,3,3,3,3,3,3} Тристерикантитусеченный 9-симплекс								302400	50400
95		т_0,1,5,6{3,3,3,3,3,3,3,3} Гексипентитусеченный 9-симплекс								151200	25200
96		т_0,2,5,6{3,3,3,3,3,3,3,3} Гексипентичный 9-симплексный								352800	50400
97		т_1,2,5,6{3,3,3,3,3,3,3,3} Бипентистерит усеченный 9-симплекс								277200	50400
98		т_0,3,5,6{3,3,3,3,3,3,3,3} Гексипентирунцинированный 9-симплекс								352800	50400
99		т_1,3,5,6{3,3,3,3,3,3,3,3} Бипентистерический 9-симплексный								491400	75600
100		т_2,3,5,6{3,3,3,3,3,3,3,3} Tristeriruncitruncated 9-simplex								252000	50400
101		т_0,4,5,6{3,3,3,3,3,3,3,3} Гексипентистерифицированный 9-симплекс								151200	25200
102		т_1,4,5,6{3,3,3,3,3,3,3,3} Бипентистерирунцинированный 9-симплекс								327600	50400
103		т_0,1,2,7{3,3,3,3,3,3,3,3} Гептицит усеченный 9-симплекс								128520	15120
104		т_0,1,3,7{3,3,3,3,3,3,3,3} Гептирунцитусеченный 9-симплексный								359100	37800
105		т_0,2,3,7{3,3,3,3,3,3,3,3} Гептирунцикантеллированный 9-симплексный								302400	37800
106		т_1,2,3,7{3,3,3,3,3,3,3,3} Бигексикантусеченный 9-симплекс								283500	37800
107		т_0,1,4,7{3,3,3,3,3,3,3,3} Гептистерит усеченный 9-симплексный								478800	50400
108		т_0,2,4,7{3,3,3,3,3,3,3,3} Гептистерический 9-симплексный								680400	75600
109		т_1,2,4,7{3,3,3,3,3,3,3,3} Бигексирунциркулированный 9-симплексный								604800	75600
110		т_0,3,4,7{3,3,3,3,3,3,3,3} Гептистерирунцинированный 9-симплекс								378000	50400
111		т_1,3,4,7{3,3,3,3,3,3,3,3} Бигексирунсианателлитный 9-симплексный								567000	75600
112		т_0,1,5,7{3,3,3,3,3,3,3,3} Гептипентусеченный 9-симплексный								321300	37800
113		т_0,2,5,7{3,3,3,3,3,3,3,3} Гептипентикантеллированный 9-симплексный								680400	75600
114		т_1,2,5,7{3,3,3,3,3,3,3,3} Бигексистерит усеченный 9-симплекс								567000	75600
115		т_0,3,5,7{3,3,3,3,3,3,3,3} Гептипентирунцинированный 9-симплекс								642600	75600
116		т_1,3,5,7{3,3,3,3,3,3,3,3} Бигексистерический 9-симплексный								907200	113400
117		т_0,4,5,7{3,3,3,3,3,3,3,3} Гептипентистерифицированный 9-симплексный								264600	37800
118		т_0,1,6,7{3,3,3,3,3,3,3,3} Гептигекситусеченный 9-симплекс								98280	15120
119		т_0,2,6,7{3,3,3,3,3,3,3,3} Гептигексикантеллированный 9-симплексный								302400	37800
120		т_1,2,6,7{3,3,3,3,3,3,3,3} Бигексипентитусеченный 9-симплекс								226800	37800
121		т_0,3,6,7{3,3,3,3,3,3,3,3} Гептигексирунцинированный 9-симплекс								428400	50400
122		т_0,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерифицированный 9-симплексный								302400	37800
123		т_0,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентеллированный 9-симплексный								98280	15120
124		т_0,1,2,8{3,3,3,3,3,3,3,3} Октикантитусеченный 9-симплекс								35280	5040
125		т_0,1,3,8{3,3,3,3,3,3,3,3} Octiruncitruncated 9-симплексный								136080	15120
126		т_0,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantellated 9-симплекс								105840	15120
127		т_0,1,4,8{3,3,3,3,3,3,3,3} Октистерит усеченный 9-симплекс								252000	25200
128		т_0,2,4,8{3,3,3,3,3,3,3,3} Octistericantellated 9-симплекс								340200	37800
129		т_0,3,4,8{3,3,3,3,3,3,3,3} Октистерирунцинированный 9-симплекс								176400	25200
130		т_0,1,5,8{3,3,3,3,3,3,3,3} Октипентусеченный 9-симплексный								252000	25200
131		т_0,2,5,8{3,3,3,3,3,3,3,3} Октипентикантеллированный 9-симплексный								504000	50400
132		т_0,3,5,8{3,3,3,3,3,3,3,3} Октипентирунцинированный 9-симплекс								453600	50400
133		т_0,1,6,8{3,3,3,3,3,3,3,3} Октигексит усеченный 9-симплекс								136080	15120
134		т_0,2,6,8{3,3,3,3,3,3,3,3} Октигексикантеллированный 9-симплекс								378000	37800
135		т_0,1,7,8{3,3,3,3,3,3,3,3} Октигепт усеченный 9-симплексный								35280	5040
136		т_0,1,2,3,4{3,3,3,3,3,3,3,3} Steriruncicantitruncated 9-simplex								136080	30240
137		т_0,1,2,3,5{3,3,3,3,3,3,3,3} Пятизубец усеченный 9-симплексный								491400	75600
138		т_0,1,2,4,5{3,3,3,3,3,3,3,3} Пентистериканитусеченный 9-симплекс								378000	75600
139		т_0,1,3,4,5{3,3,3,3,3,3,3,3} Пентистерирункоусеченный 9-симплексный								378000	75600
140		т_0,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantellated 9-симплекс								378000	75600
141		т_1,2,3,4,5{3,3,3,3,3,3,3,3} Bisteriruncicantitruncated 9-simplex								340200	75600
142		т_0,1,2,3,6{3,3,3,3,3,3,3,3} Гексирунциантитусеченный 9-симплекс								756000	100800
143		т_0,1,2,4,6{3,3,3,3,3,3,3,3} Гексистерикантитусеченный 9-симплекс								1058400	151200
144		т_0,1,3,4,6{3,3,3,3,3,3,3,3} Гексистерирунциркулированный 9-симплексный								982800	151200
145		т_0,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantellated 9-симплекс								982800	151200
146		т_1,2,3,4,6{3,3,3,3,3,3,3,3} Бипентирунцинатусеченный 9-симплекс								907200	151200
147		т_0,1,2,5,6{3,3,3,3,3,3,3,3} Гексипентикантитусеченный 9-симплекс								554400	100800
148		т_0,1,3,5,6{3,3,3,3,3,3,3,3} Гексипентирноусеченный 9-симплекс								907200	151200
149		т_0,2,3,5,6{3,3,3,3,3,3,3,3} Шестигранникантеллированный 9-симплекс								831600	151200
150		т_1,2,3,5,6{3,3,3,3,3,3,3,3} Бипентистерический усеченный 9-симплекс								756000	151200
151		т_0,1,4,5,6{3,3,3,3,3,3,3,3} Гексипентистерит усеченный 9-симплекс								554400	100800
152		т_0,2,4,5,6{3,3,3,3,3,3,3,3} Гексипентистерический 9-симплексный								907200	151200
153		т_1,2,4,5,6{3,3,3,3,3,3,3,3} Бипентистеры, усеченные, 9-симплексные								756000	151200
154		т_0,3,4,5,6{3,3,3,3,3,3,3,3} Гексипентистерирунцинированный 9-симплекс								554400	100800
155		т_1,3,4,5,6{3,3,3,3,3,3,3,3} Бипентистерирункикантеллированный 9-симплексный								831600	151200
156		т_2,3,4,5,6{3,3,3,3,3,3,3,3} Tristeriruncicantitruncated 9-simplex								453600	100800
157		т_0,1,2,3,7{3,3,3,3,3,3,3,3} Гептирунциентитусеченный 9-симплексный								567000	75600
158		т_0,1,2,4,7{3,3,3,3,3,3,3,3} Гептистерикантитусеченный 9-симплексный								1209600	151200
159		т_0,1,3,4,7{3,3,3,3,3,3,3,3} Гептистерирунциркулированный 9-симплексный								1058400	151200
160		т_0,2,3,4,7{3,3,3,3,3,3,3,3} Гептистерирунксикантеллированный 9-симплексный								1058400	151200
161		т_1,2,3,4,7{3,3,3,3,3,3,3,3} Бигексирунцианитусеченный 9-симплекс								982800	151200
162		т_0,1,2,5,7{3,3,3,3,3,3,3,3} Гептипентикантитусеченный 9-симплекс								1134000	151200
163		т_0,1,3,5,7{3,3,3,3,3,3,3,3} Гептипентирункусеченный 9-симплексный								1701000	226800
164		т_0,2,3,5,7{3,3,3,3,3,3,3,3} Гептипентирунцикантеллированный 9-симплексный								1587600	226800
165		т_1,2,3,5,7{3,3,3,3,3,3,3,3} Бигексистерикантитроусеченный 9-симплекс								1474200	226800
166		т_0,1,4,5,7{3,3,3,3,3,3,3,3} Гептипентистерит усеченный 9-симплексный								982800	151200
167		т_0,2,4,5,7{3,3,3,3,3,3,3,3} Гептипентистерический 9-симплексный								1587600	226800
168		т_1,2,4,5,7{3,3,3,3,3,3,3,3} Бигексистерирунциркулированный 9-симплексный								1360800	226800
169		т_0,3,4,5,7{3,3,3,3,3,3,3,3} Гептипентистерирунцинированный 9-симплекс								982800	151200
170		т_1,3,4,5,7{3,3,3,3,3,3,3,3} Бигексистерирунсианателлитный 9-симплексный								1474200	226800
171		т_0,1,2,6,7{3,3,3,3,3,3,3,3} Гептигексикант усеченный 9-симплекс								453600	75600
172		т_0,1,3,6,7{3,3,3,3,3,3,3,3} Гептигексирунциркулированный 9-симплексный								1058400	151200
173		т_0,2,3,6,7{3,3,3,3,3,3,3,3} Гептигексирунцианский антеллированный 9-симплексный								907200	151200
174		т_1,2,3,6,7{3,3,3,3,3,3,3,3} Бигексипентикантитроусеченный 9-симплекс								831600	151200
175		т_0,1,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерит усеченный 9-симплексный								1058400	151200
176		т_0,2,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерический 9-симплексный								1587600	226800
177		т_1,2,4,6,7{3,3,3,3,3,3,3,3} Бигексипентирноусеченный 9-симплекс								1360800	226800
178		т_0,3,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерирунцинированный 9-симплекс								907200	151200
179		т_0,1,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентитусеченный 9-симплекс								453600	75600
180		т_0,2,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентикантеллированный 9-симплексный								1058400	151200
181		т_0,3,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентирунцинированный 9-симплекс								1058400	151200
182		т_0,4,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентистерифицированный 9-симплекс								453600	75600
183		т_0,1,2,3,8{3,3,3,3,3,3,3,3} Octiruncicantitruncated 9-симплекс								196560	30240
184		т_0,1,2,4,8{3,3,3,3,3,3,3,3} Октистерикантитусеченный 9-симплекс								604800	75600
185		т_0,1,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncitruncated 9-симплекс								491400	75600
186		т_0,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantellated 9-симплекс								491400	75600
187		т_0,1,2,5,8{3,3,3,3,3,3,3,3} Октипентикантитроусеченный 9-симплекс								856800	100800
188		т_0,1,3,5,8{3,3,3,3,3,3,3,3} Октипентироусеченный 9-симплексный								1209600	151200
189		т_0,2,3,5,8{3,3,3,3,3,3,3,3} Октипятизубчато-сочлененные 9-симплексные								1134000	151200
190		т_0,1,4,5,8{3,3,3,3,3,3,3,3} Октипентистерит усеченный 9-симплексный								655200	100800
191		т_0,2,4,5,8{3,3,3,3,3,3,3,3} Октипентистерический 9-симплексный								1058400	151200
192		т_0,3,4,5,8{3,3,3,3,3,3,3,3} Октипентистерирунцинированный 9-симплекс								655200	100800
193		т_0,1,2,6,8{3,3,3,3,3,3,3,3} Octihexicantitruncated 9-simplex								604800	75600
194		т_0,1,3,6,8{3,3,3,3,3,3,3,3} Октигексирунцирункусеченный 9-симплексный								1285200	151200
195		т_0,2,3,6,8{3,3,3,3,3,3,3,3} Октигексирунцианский, 9-симплексный								1134000	151200
196		т_0,1,4,6,8{3,3,3,3,3,3,3,3} Октигексистерит усеченный 9-симплексный								1209600	151200
197		т_0,2,4,6,8{3,3,3,3,3,3,3,3} Octihexistericantellated 9-симплекс								1814400	226800
198		т_0,1,5,6,8{3,3,3,3,3,3,3,3} Октигексипентусеченный 9-симплекс								491400	75600
199		т_0,1,2,7,8{3,3,3,3,3,3,3,3} Octihepticantitruncated 9-simplex								196560	30240
200		т_0,1,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncitruncated 9-simplex								604800	75600
201		т_0,1,4,7,8{3,3,3,3,3,3,3,3} Октигептистерит усеченный 9-симплексный								856800	100800
202		т_0,1,2,3,4,5{3,3,3,3,3,3,3,3} Pentisteriruncicantitruncated 9-simplex								680400	151200
203		т_0,1,2,3,4,6{3,3,3,3,3,3,3,3} Hexisteriruncicantitruncated 9-simplex								1814400	302400
204		т_0,1,2,3,5,6{3,3,3,3,3,3,3,3} Гексипентирунциансусеченный 9-симплекс								1512000	302400
205		т_0,1,2,4,5,6{3,3,3,3,3,3,3,3} Гексипентистерикантитроусеченный 9-симплекс								1512000	302400
206		т_0,1,3,4,5,6{3,3,3,3,3,3,3,3} Гексипентистер, усеченный, 9-симплексный								1512000	302400
207		т_0,2,3,4,5,6{3,3,3,3,3,3,3,3} Гексипентистер (гексипентистер) - трехсторонний 9-симплексный								1512000	302400
208		т_1,2,3,4,5,6{3,3,3,3,3,3,3,3} Бипентистерирунксикантусеченный 9-симплекс								1360800	302400
209		т_0,1,2,3,4,7{3,3,3,3,3,3,3,3} Гептистерирункитусеченный 9-симплексный								1965600	302400
210		т_0,1,2,3,5,7{3,3,3,3,3,3,3,3} Гептипентирунциентусеченный 9-симплексный								2948400	453600
211		т_0,1,2,4,5,7{3,3,3,3,3,3,3,3} Гептипентистерикантитроусеченный 9-симплексный								2721600	453600
212		т_0,1,3,4,5,7{3,3,3,3,3,3,3,3} Гептипентистер - усеченный 9-симплексный								2721600	453600
213		т_0,2,3,4,5,7{3,3,3,3,3,3,3,3} Гептипентистер - несуществующий 9-симплексный								2721600	453600
214		т_1,2,3,4,5,7{3,3,3,3,3,3,3,3} Бигексистерирунксикантусеченный 9-симплекс								2494800	453600
215		т_0,1,2,3,6,7{3,3,3,3,3,3,3,3} Гептигексируницинтусеченный 9-симплекс								1663200	302400
216		т_0,1,2,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерикантитроусеченный 9-симплексный								2721600	453600
217		т_0,1,3,4,6,7{3,3,3,3,3,3,3,3} Гептигексистерирунция усеченный 9-симплексный								2494800	453600
218		т_0,2,3,4,6,7{3,3,3,3,3,3,3,3} Гептигексистер - несуществующий 9-симплексный								2494800	453600
219		т_1,2,3,4,6,7{3,3,3,3,3,3,3,3} Бигексипентируницинтитусеченный 9-симплекс								2268000	453600
220		т_0,1,2,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентикантитроусеченный 9-симплекс								1663200	302400
221		т_0,1,3,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентирноусеченный 9-симплекс								2721600	453600
222		т_0,2,3,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентирунциатантеллированный 9-симплекс								2494800	453600
223		т_1,2,3,5,6,7{3,3,3,3,3,3,3,3} Бигексипентистерикантитроусеченный 9-симплекс								2268000	453600
224		т_0,1,4,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентистерит усеченный 9-симплекс								1663200	302400
225		т_0,2,4,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентистерический антеллированный 9-симплексный								2721600	453600
226		т_0,3,4,5,6,7{3,3,3,3,3,3,3,3} Гептигексипентистерирунцинированный 9-симплекс								1663200	302400
227		т_0,1,2,3,4,8{3,3,3,3,3,3,3,3} Octisteriruncicantitruncated 9-simplex								907200	151200
228		т_0,1,2,3,5,8{3,3,3,3,3,3,3,3} Октипентирусусеченное усеченное 9-симплексное								2116800	302400
229		т_0,1,2,4,5,8{3,3,3,3,3,3,3,3} Октипентистерикантусеченный 9-симплекс								1814400	302400
230		т_0,1,3,4,5,8{3,3,3,3,3,3,3,3} Октипентистер, усеченный, 9-симплексный								1814400	302400
231		т_0,2,3,4,5,8{3,3,3,3,3,3,3,3} Октипентистер (октипентистер) - трехсторонний, 9-симплексный								1814400	302400
232		т_0,1,2,3,6,8{3,3,3,3,3,3,3,3} Октигексирунцианитусеченный 9-симплекс								2116800	302400
233		т_0,1,2,4,6,8{3,3,3,3,3,3,3,3} Октигексистерикантитроусеченный 9-симплексный								3175200	453600
234		т_0,1,3,4,6,8{3,3,3,3,3,3,3,3} Октигексистер, усеченный 9-симплексный								2948400	453600
235		т_0,2,3,4,6,8{3,3,3,3,3,3,3,3} Октигексистер (октигексистер) - разветвленный 9-симплексный								2948400	453600
236		т_0,1,2,5,6,8{3,3,3,3,3,3,3,3} Октигексипентикантитроусеченный 9-симплекс								1814400	302400
237		т_0,1,3,5,6,8{3,3,3,3,3,3,3,3} Октигексипентирноусеченный 9-симплекс								2948400	453600
238		т_0,2,3,5,6,8{3,3,3,3,3,3,3,3} Октигексипентирунциатантеллированный 9-симплекс								2721600	453600
239		т_0,1,4,5,6,8{3,3,3,3,3,3,3,3} Октигексипентистер усеченный 9-симплекс								1814400	302400
240		т_0,1,2,3,7,8{3,3,3,3,3,3,3,3} Octiheptiruncicantitruncated 9-симплекс								907200	151200
241		т_0,1,2,4,7,8{3,3,3,3,3,3,3,3} Октигептистерикантитроусеченный 9-симплексный								2116800	302400
242		т_0,1,3,4,7,8{3,3,3,3,3,3,3,3} Октигептистер - усеченный 9-симплексный								1814400	302400
243		т_0,1,2,5,7,8{3,3,3,3,3,3,3,3} Октигептипентикантитроусеченный 9-симплекс								2116800	302400
244		т_0,1,3,5,7,8{3,3,3,3,3,3,3,3} Октигептипентирукоусеченный 9-симплексный								3175200	453600
245		т_0,1,2,6,7,8{3,3,3,3,3,3,3,3} Октигептигексикант усеченный 9-симплекс								907200	151200
246		т_{0,1,2,3,4,5,6}{3,3,3,3,3,3,3,3} Гексипентистер, усеченный, 9-симплексный								2721600	604800
247		т_{0,1,2,3,4,5,7}{3,3,3,3,3,3,3,3} Гептипентистер - усеченный 9-симплексный								4989600	907200
248		т_{0,1,2,3,4,6,7}{3,3,3,3,3,3,3,3} Гептигексистерирункитусеченный 9-симплекс								4536000	907200
249		т_{0,1,2,3,5,6,7}{3,3,3,3,3,3,3,3} Гептигексипентируницинтитусеченный 9-симплекс								4536000	907200
250		т_{0,1,2,4,5,6,7}{3,3,3,3,3,3,3,3} Гептигексипентистерикантитроусеченный 9-симплекс								4536000	907200
251		т_{0,1,3,4,5,6,7}{3,3,3,3,3,3,3,3} Гептигексипентистер, усеченный 9-симплекс								4536000	907200
252		т_{0,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Гептигексипентистер - несуществующий 9-симплексный								4536000	907200
253		т_{1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Бигексипентистер-унцианитусеченный 9-симплекс								4082400	907200
254		т_{0,1,2,3,4,5,8}{3,3,3,3,3,3,3,3} Octipentisteriruncicantitruncated 9-simplex								3326400	604800
255		т_{0,1,2,3,4,6,8}{3,3,3,3,3,3,3,3} Octihexisteriruncicantitruncated 9-simplex								5443200	907200
256		т_{0,1,2,3,5,6,8}{3,3,3,3,3,3,3,3} Октигексипентирунцинус усеченный 9-симплекс								4989600	907200
257		т_{0,1,2,4,5,6,8}{3,3,3,3,3,3,3,3} Октигексипентистерикантитроусеченный 9-симплекс								4989600	907200
258		т_{0,1,3,4,5,6,8}{3,3,3,3,3,3,3,3} Октигексипентистер, усеченный 9-симплекс								4989600	907200
259		т_{0,2,3,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantellated 9-simplex								4989600	907200
260		т_{0,1,2,3,4,7,8}{3,3,3,3,3,3,3,3} Octiheptisteriruncicantitruncated 9-simplex								3326400	604800
261		т_{0,1,2,3,5,7,8}{3,3,3,3,3,3,3,3} Октигептипентирунцинитусеченный 9-симплекс								5443200	907200
262		т_{0,1,2,4,5,7,8}{3,3,3,3,3,3,3,3} Октигептипентистерикантитроусеченный 9-симплекс								4989600	907200
263		т_{0,1,3,4,5,7,8}{3,3,3,3,3,3,3,3} Октигептипентистер, усеченный 9-симплекс								4989600	907200
264		т_{0,1,2,3,6,7,8}{3,3,3,3,3,3,3,3} Октигептигексирунцианитусеченный 9-симплекс								3326400	604800
265		т_{0,1,2,4,6,7,8}{3,3,3,3,3,3,3,3} Октигептигексистерикантитроусеченный 9-симплекс								5443200	907200
266		т_{0,1,2,3,4,5,6,7}{3,3,3,3,3,3,3,3} Гептигексипентистер - усеченный 9-симплекс								8164800	1814400
267		т_{0,1,2,3,4,5,6,8}{3,3,3,3,3,3,3,3} Octihexipentisteriruncicantitruncated 9-simplex								9072000	1814400
268		т_{0,1,2,3,4,5,7,8}{3,3,3,3,3,3,3,3} Октигептипентистерируницинтусеченный 9-симплекс								9072000	1814400
269		т_{0,1,2,3,4,6,7,8}{3,3,3,3,3,3,3,3} Octiheptihexisteriruncicantitruncated 9-simplex								9072000	1814400
270		т_{0,1,2,3,5,6,7,8}{3,3,3,3,3,3,3,3} Октигептигексипентирунциентусеченный 9-симплекс								9072000	1814400
271		т_{0,1,2,3,4,5,6,7,8}{3,3,3,3,3,3,3,3} Омнитусеченный 9-симплекс								16329600	3628800

B₉ семья

Всего существует 511 форм, основанных на всех перестановках Диаграммы Кокстера-Дынкина с одним или несколькими кольцами.

Ниже показаны одиннадцать случаев: девять исправленный формы и 2 усечения. Названия акронимов в стиле Bowers приведены в скобках для перекрестных ссылок. Названия акронимов в стиле Bowers приведены в скобках для перекрестных ссылок.

#	График	Диаграмма Кокстера-Дынкина Символ Шлефли Имя	Количество элементов
#	График	Диаграмма Кокстера-Дынкина Символ Шлефли Имя	8 лиц	7 лиц	6 лиц	5 лиц	4 лица	Клетки	Лица	Края	Вершины
1		т₀{4,3,3,3,3,3,3,3} 9-куб (энне)	18	144	672	2016	4032	5376	4608	2304	512
2		т_0,1{4,3,3,3,3,3,3,3} Усеченный 9-куб (десять)								2304	4608
3		т₁{4,3,3,3,3,3,3,3} Ректифицированный 9-куб (Ren)								18432	2304
4		т₂{4,3,3,3,3,3,3,3} Биректифицированный 9-куб (сарай)								64512	4608
5		т₃{4,3,3,3,3,3,3,3} Триректифицированный 9-куб (карьер)								96768	5376
6		т₄{4,3,3,3,3,3,3,3} Quadrirectified 9-куб (навигация) (Квадриректифицированный 9-ортоплекс)								80640	4032
7		т₃{3,3,3,3,3,3,3,4} Триректифицированный 9-ортоплекс (tarv)								40320	2016
8		т₂{3,3,3,3,3,3,3,4} Биректифицированный 9-ортоплекс (брав)								12096	672
9		т₁{3,3,3,3,3,3,3,4} Ректифицированный 9-ортоплекс (riv)								2016	144
10		т_0,1{3,3,3,3,3,3,3,4} Усеченный 9-ортоплекс (tiv)								2160	288
11		т₀{3,3,3,3,3,3,3,4} 9-ортоплекс (vee)	512	2304	4608	5376	4032	2016	672	144	18

D₉ семья

D₉ семья имеет симметрию порядка 92897280 (9 факториал × 2⁸).

Это семейство состоит из 3 × 128−1 = 383 однородных многогранников Витоффа, созданных путем пометки одного или нескольких узлов D₉ Диаграмма Кокстера-Дынкина. Из них 255 (2 × 128−1) повторяются из B₉ family и 128 уникальны для этого семейства, с восемью формами с 1 или 2 кольцами, перечисленными ниже. Названия акронимов в стиле Bowers приведены в скобках для перекрестных ссылок.

#	Самолет Кокстера графики											Диаграмма Кокстера-Дынкина Символ Шлефли	Базовая точка (Альтернативно подписано)	Количество элементов									Circumrad
#	B₉	D₉	D₈	D₇	D₆	D₅	D₄	D₃	А₇	А₅	А₃	Диаграмма Кокстера-Дынкина Символ Шлефли	Базовая точка (Альтернативно подписано)	8	7	6	5	4	3	2	1	0	Circumrad
1												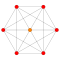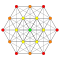9-полукруглый (Henne)	(1,1,1,1,1,1,1,1,1)	274	2448	9888	23520	36288	37632	21404	4608	256	1.0606601
2								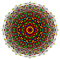				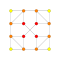Усеченный 9-полукуб (затем)	(1,1,3,3,3,3,3,3,3)								69120	9216	2.8504384
3								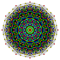				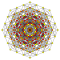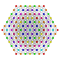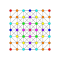Сквозной 9-полукуб	(1,1,1,3,3,3,3,3,3)								225792	21504	2.6692696
4		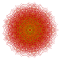										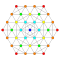Runcinated 9-demicube	(1,1,1,1,3,3,3,3,3)								419328	32256	2.4748735
5												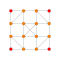Стерилизованный 9-полукруглый	(1,1,1,1,1,3,3,3,3)								483840	32256	2.2638462
6												Пятиугольник 9-полукуб	(1,1,1,1,1,1,3,3,3)								354816	21504	2.0310094
7												Проклятый 9-demicube	(1,1,1,1,1,1,1,3,3)								161280	9216	1.7677668
8												Зубчатый 9-полукуб	(1,1,1,1,1,1,1,1,3)								41472	2304	1.4577379

Обычные и однородные соты

Соответствия диаграмм Кокстера-Дынкина между семействами и высшая симметрия внутри диаграмм. Узлы одного цвета в каждом ряду представляют собой одинаковые зеркала. Черные узлы в переписке не активны.

Есть пять основных аффинных Группы Кокстера которые генерируют регулярные и однородные мозаики в 8-мерном пространстве:

#	Группа Кокстера		Формы
1	${displaystyle {ilde {A}} _ {8}}$	[3^[9]]	45
2	${displaystyle {ilde {C}} _ {8}}$	[4,3⁶,4]	271
3	${displaystyle {ilde {B}} _ {8}}$	ч [4,3⁶,4] [4,3⁵,3^1,1]	383 (128 новых)
4	${displaystyle {ilde {D}} _ {8}}$	q [4,3⁶,4] [3^1,1,3⁴,3^1,1]	155 (15 новых)
5	${displaystyle {ilde {E}} _ {8}}$	[3^5,2,1]	511

Обычные и однородные мозаики включают:

${displaystyle {ilde {A}} _ {8}}$ ${{ilde {A}}} _ {8}$ 45 уникально окольцованных форм
- 8-симплексные соты: {3^[9]}
${displaystyle {ilde {C}} _ {8}}$ ${{ilde {C}}} _ {8}$ 271 однозначно окольцованная форма
- Обычный 8-кубовые соты: {4,3⁶,4},
${displaystyle {ilde {B}} _ {8}}$ ${{ilde {B}}} _ {8}$ : 383 формы с уникальными кольцами, 255 общие с ${displaystyle {ilde {C}} _ {8}}$ ${{ilde {C}}} _ {8}$ , 128 новых
- Сота с 8 полукубами: h {4,3⁶, 4} или {3^1,1,3⁵,4}, или же
${displaystyle {ilde {D}} _ {8}}$ , [3^1,1,3⁴,3^1,1]: 155 уникальных перестановок колец и 15 новых, первые, , Кокстер назвал четверть 8-кубовые соты, представляя как q {4,3⁶, 4} или qδ₉.
${displaystyle {ilde {E}} _ {8}}$ ${ilde {E}} _ {8}$ 511 форм

Регулярные и однородные гиперболические соты

Не существует компактных гиперболических групп Кокстера ранга 9, групп, которые могут порождать соты со всеми конечными гранями, и конечных вершина фигуры. Однако есть 4 некомпактные гиперболические группы Кокстера ранга 9, каждая из которых порождает однородные соты в 8-пространстве как перестановки колец диаграмм Кокстера.

${displaystyle {ar {P}} _ {8}}$ = [3,3^[8]]:	${displaystyle {ar {Q}} _ {8}}$ = [3^1,1,3³,3^2,1]:	${displaystyle {ar {S}} _ {8}}$ = [4,3⁴,3^2,1]:	${displaystyle {ar {T}} _ {8}}$ = [3^4,3,1]:

внешняя ссылка

Имена многогранников
Многогранники разной размерности, Джонатан Бауэрс
Многомерный глоссарий
Глоссарий по гиперпространству, Георгий Ольшевский.

v т е Фундаментальный выпуклый обычный и однородные многогранники в размерах 2–10
Семья	А_п	B_п	я₂(п) / D_п	E₆ / E₇ / E₈ / F₄ / грамм₂	ЧАС_п
Правильный многоугольник	Треугольник	Квадрат	п-угольник	Шестиугольник	Пентагон
Равномерный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный 4-многогранник	5-элементный	16 ячеек • Тессеракт	Demitesseract	24-элементный	120 ячеек • 600 ячеек
Равномерный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-полукуб
Равномерный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-полукуб	1₂₂ • 2₂₁
Равномерный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-полукруглый	1₃₂ • 2₃₁ • 3₂₁
Равномерный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-полукруглый	1₄₂ • 2₄₁ • 4₂₁
Равномерный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-полукруглый
Равномерный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-полукуб
Униформа п-многогранник	п-симплекс	п-ортоплекс • п-куб	п-полукуб	1_k2 • 2_k1 • k₂₁	п-пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${displaystyle {ilde {A}} _ {n-1}}$	${displaystyle {ilde {C}} _ {n-1}}$	${displaystyle {ilde {B}} _ {n-1}}$	${displaystyle {ilde {D}} _ {n-1}}$	${displaystyle {ilde {G}} _ {2}}$ / ${displaystyle {ilde {F}} _ {4}}$ / ${displaystyle {ilde {E}} _ {n-1}}$
E²	Равномерная черепица	{3^[3]}	δ₃	hδ₃	qδ₃	Шестиугольный
E³	Равномерно выпуклые соты	{3^[4]}	δ₄	hδ₄	qδ₄
E⁴	Равномерные 4-соты	{3^[5]}	δ₅	hδ₅	qδ₅	24-ячеечные соты
E⁵	Равномерные 5-соты	{3^[6]}	δ₆	hδ₆	qδ₆
E⁶	Равномерные 6-соты	{3^[7]}	δ₇	hδ₇	qδ₇	2₂₂
E⁷	Равномерные 7-соты	{3^[8]}	δ₈	hδ₈	qδ₈	1₃₃ • 3₃₁
E⁸	Равномерные 8-соты	{3^[9]}	δ₉	hδ₉	qδ₉	1₅₂ • 2₅₁ • 5₂₁
E⁹	Равномерные 9-соты	{3^[10]}	δ₁₀	hδ₁₀	qδ₁₀
E^п-1	Униформа (п-1)-соты	{3^[n]}	δ_п	hδ_п	qδ_п	1_k2 • 2_k1 • k₂₁

[richeson-1] а ^б ^c Richeson, D .; Драгоценный камень Эйлера: формула многогранника и рождение топоплогии, Принстон, 2008.

[1]

Navigation

Navigation

Themenportale

WikiDer > Равномерный 9-многогранник

Содержание

Правильные 9-многогранники

Эйлерова характеристика

Равномерные 9-многогранники фундаментальными группами Кокстера

А₉ семья

B₉ семья

D₉ семья

Обычные и однородные соты

Регулярные и однородные гиперболические соты

Рекомендации

внешняя ссылка

Navigation

WikiDer > Равномерный 9-многогранник

Правильные 9-многогранники

Эйлерова характеристика

Равномерные 9-многогранники фундаментальными группами Кокстера

А9 семья

B9 семья

D9 семья

Обычные и однородные соты

Регулярные и однородные гиперболические соты

Рекомендации

внешняя ссылка

А₉ семья

B₉ семья

D₉ семья