WikiDer > Вейвлет-преобразование

Wavelet transform

Пример 2D дискретное вейвлет-преобразование что используется в JPEG2000.

В математика, а серия вейвлетов является представлением квадратично интегрируемый (настоящий- или же сложный-значен) функция определенным ортонормированный серии созданный вейвлет. В этой статье дается формальное математическое определение ортонормированный вейвлет и из интегральное вейвлет-преобразование.^[1]^[2]^[3]^[4]

Определение

Функция ${ Displaystyle psi , in , L ^ {2} ( mathbb {R})}$ называется ортонормированный вейвлет если его можно использовать для определения Базис Гильберта, это полный ортонормированная система, для Гильбертово пространство ${ Displaystyle L ^ {2} влево ( mathbb {R} right)}$ из квадратично интегрируемый функции.

Базис Гильберта строится как семейство функций ${ Displaystyle { psi _ {jk}: , j, , k , in , mathbb {Z} }}$ посредством диадический переводы и расширение из ${ displaystyle psi ,}$ ,

{ Displaystyle psi _ {jk} (x) = 2 ^ { frac {j} {2}} psi left (2 ^ {j} x-k right) ,}

для целых чисел ${ Displaystyle J, , к , в , mathbb {Z}}$ .

Если по стандарту внутренний продукт на ${ Displaystyle L ^ {2} влево ( mathbb {R} right)}$ ,

{ displaystyle langle f, g rangle = int _ {- infty} ^ { infty} f (x) { overline {g (x)}} dx}

это семейство ортонормировано, это ортонормированная система:

{ displaystyle { begin {align} langle psi _ {jk}, psi _ {lm} rangle & = int _ {- infty} ^ { infty} psi _ {jk} (x) { overline { psi _ {lm} (x)}} dx & = delta _ {jl} delta _ {km} end {выравнивается}}}

куда ${ displaystyle delta _ {jl} ,}$ это Дельта Кронекера.

Полнота удовлетворяется, если каждая функция ${ Displaystyle е , в , L ^ {2} влево ( mathbb {R} right)}$ может быть расширен в основе как

{ displaystyle f (x) = sum _ {j, k = - infty} ^ { infty} c_ {jk} psi _ {jk} (x)}

со сходимостью ряда понимается сходимость по норме. Такое представление ж известен как серия вейвлетов. Это означает, что ортонормированный вейвлет самодвойственный.

В интегральное вейвлет-преобразование это интегральное преобразование определяется как

{ displaystyle left [W _ { psi} f right] (a, b) = { frac {1} { sqrt {| a |}}} int _ {- infty} ^ { infty} { overline { psi left ({ frac {xb} {a}} right)}} f (x) dx ,}

В вейвлет-коэффициенты ${ displaystyle c_ {jk}}$ тогда даются

{ displaystyle c_ {jk} = left [W _ { psi} f right] left (2 ^ {- j}, k2 ^ {- j} right)}

Здесь, ${ displaystyle a = 2 ^ {- j}}$ называется двоичное расширение или диадическое расширение, и ${ displaystyle b = k2 ^ {- j}}$ это двоичный или диадическая позиция.

Принцип

Основная идея вейвлет-преобразований состоит в том, что преобразование должно допускать только изменения во времени, но не в форме. На это влияет выбор подходящих базовых функций, которые позволяют это сделать.^[как?] Ожидается, что изменения в увеличении времени будут соответствовать соответствующей частоте анализа базовой функции. На основе принцип неопределенности обработки сигналов,

{ displaystyle Delta t Delta omega geq { frac {1} {2}}}

куда ${ displaystyle t}$ представляет время и ${ displaystyle omega}$ угловая частота ( ${ displaystyle omega = 2 pi f}$ , куда ${ displaystyle f}$ - временная частота).

Чем выше требуемое разрешение по времени, тем ниже должно быть разрешение по частоте. Чем больше объем анализа окна выбирается, тем больше значение ${ displaystyle Delta t}$ ^[как?].

Когда ${ displaystyle Delta t}$ большой,

Плохое временное разрешение
Хорошее частотное разрешение
Низкая частота, большой коэффициент масштабирования

Когда ${ displaystyle Delta t}$ маленький

Хорошее временное разрешение
Плохое частотное разрешение
Высокая частота, небольшой коэффициент масштабирования

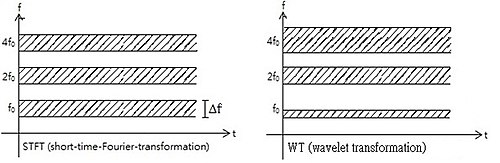
Другими словами, базисная функция ${ displaystyle psi}$ можно рассматривать как импульсную характеристику системы, в которой функция ${ Displaystyle х (т)}$ был отфильтрован. Преобразованный сигнал предоставляет информацию о времени и частоте. Следовательно, вейвлет-преобразование содержит информацию, аналогичную кратковременное преобразование Фурье, но с дополнительными особыми свойствами вейвлетов, которые проявляются с разрешением по времени на более высоких частотах анализа базисной функции. Разница во временном разрешении на возрастающих частотах для преобразование Фурье и вейвлет-преобразование показано ниже. Однако обратите внимание, что разрешение по частоте уменьшается с увеличением частот, в то время как разрешение по времени увеличивается. Это следствие Принцип неопределенности Фурье некорректно отображается на рисунке.

Это показывает, что вейвлет-преобразование имеет хорошее временное разрешение на высоких частотах, в то время как для медленно меняющихся функций разрешение по частоте замечательное.

Другой пример: анализ трех наложенных синусоидальных сигналов. ${ displaystyle y (t) ; = ; sin (2 pi f_ {0} t) ; + ; sin (4 pi f_ {0} t) ; + ; sin (8 pi f_ {0} t)}$ с STFT и вейвлет-преобразованием.

Вейвлет-сжатие

Вейвлет-сжатие это форма Сжатие данных хорошо подходит для сжатие изображений (иногда также сжатие видео и сжатие звука). Известные реализации: JPEG 2000, DjVu и ECW для неподвижных изображений, CineForm, и BBC Дирак. Цель состоит в том, чтобы хранить данные изображения на как можно меньшем пространстве в файл. Вейвлет-сжатие может быть без потерь или с потерями.^[5] Вейвлет-кодирование - это вариант дискретное косинусное преобразование (DCT) кодирование, использующее вейвлеты вместо блочного алгоритма DCT.^[6]

Используя вейвлет-преобразование, методы вейвлет-сжатия подходят для представления переходные процессы, например звуки перкуссии в аудио или высокочастотные компоненты в двухмерных изображениях, например изображение звезд на ночном небе. Это означает, что переходные элементы сигнала данных могут быть представлены меньшим объемом информации, чем было бы, если бы какое-либо другое преобразование, такое как более распространенное дискретное косинусное преобразование, был использован.

Дискретное вейвлет-преобразование успешно применяется для сжатия сигналов электрокардиографа (ЭКГ).^[7] В этой работе высокая корреляция между соответствующими вейвлет-коэффициентами сигналов последовательных сердечных циклов используется с использованием линейного предсказания.

Вейвлет-сжатие не подходит для всех видов данных: характеристики переходного сигнала означают хорошее вейвлет-сжатие, в то время как гладкие периодические сигналы лучше сжимаются другими методами, особенно традиционным гармоническим сжатием (частотная область, например, преобразованием Фурье и т.п.).

Видеть Дневник разработчика x264: проблемы с вейвлетами (2010) для обсуждения практических вопросов современных методов использования вейвлетов для сжатия видео.

Метод

Сначала применяется вейвлет-преобразование. Это производит столько же коэффициенты как есть пиксели в изображении (то есть сжатия еще нет, так как это всего лишь преобразование). Эти коэффициенты затем можно легче сжать, потому что информация статистически сконцентрирована всего в нескольких коэффициентах. Этот принцип называется преобразование кодирования. После этого коэффициенты находятся квантованный и квантованные значения закодированная энтропией и / или длина серии закодирована.

Некоторые одномерные и двухмерные приложения вейвлет-сжатия используют технику, называемую «следы вейвлетов».^[8]^[9]

Сравнение с преобразованием Фурье и частотно-временным анализом

Преобразовать	Представление	Вход
преобразование Фурье	${ displaystyle { hat {f}} ( xi) = int _ {- infty} ^ { infty} f (x) e ^ {- 2 pi ix xi} , dx}$	${ Displaystyle xi}$ частота
Частотно-временной анализ	${ Displaystyle X (т, е)}$	${ displaystyle t}$ время; ${ displaystyle f}$ частота
Вейвлет-преобразование	${ displaystyle X (a, b) = { frac {1} { sqrt {a}}} int _ {- infty} ^ { infty} { overline { Psi left ({ frac { tb} {a}} right)}} x (t) , dt}$	${ displaystyle a}$ масштабирование; ${ displaystyle b}$ коэффициент временного сдвига

Вейвлеты имеют некоторые небольшие преимущества перед преобразованиями Фурье в сокращении объема вычислений при исследовании конкретных частот. Однако они редко бывают более чувствительными, и действительно Вейвлет Морле математически идентичен кратковременное преобразование Фурье с использованием функции окна Гаусса.^[10] Исключение составляет поиск сигналов известной несинусоидальной формы (например, сердцебиение); в этом случае использование согласованных вейвлетов может превзойти стандартный анализ STFT / Морле.^[11]

Другие практические приложения

Вейвлет-преобразование может предоставить нам частоту сигналов и время, связанные с этими частотами, что делает его очень удобным для его применения во многих областях. Например, обработка сигналов ускорений для анализа походки,^[12] для обнаружения неисправностей,^[13] для разработки кардиостимуляторов малой мощности, а также для сверхширокополосной (UWB) беспроводной связи.^[14]^[15]^[16]

Дискретность ${ displaystyle c- tau}$ ось
Применена следующая дискретизация частоты и времени:
${ displaystyle { begin {align} c_ {n} & = c_ {0} ^ {n} tau _ {m} & = m cdot T cdot c_ {0} ^ {n} end { выровнено}}}$
Приводя к вейвлетам формы, дискретная формула для базисного вейвлета:
${ displaystyle Psi (k, n, m) = { frac {1} { sqrt {c_ {0} ^ {n}}}} cdot Psi left [{ frac {k-mc_ {0} } ^ {n}} {c_ {0} ^ {n}}} T right] = { frac {1} { sqrt {c_ {0} ^ {n}}}} cdot Psi left [ left ({ frac {k} {c_ {0} ^ {n}}} - m right) T right]}$
Такие дискретные вейвлеты можно использовать для преобразования:
${ displaystyle Y_ {DW} (n, m) = { frac {1} { sqrt {c_ {0} ^ {n}}}} cdot sum _ {k = 0} ^ {K-1} y (k) cdot Psi left [ left ({ frac {k} {c_ {0} ^ {n}}} - m right) T right]}$
Реализация через БПФ (быстрое преобразование Фурье)
Как видно из представления вейвлет-преобразования (показано ниже)
${ Displaystyle Y_ {W} (c, tau) = { frac {1} { sqrt {c}}} cdot int _ {- infty} ^ { infty} y (t) cdot Psi left ({ frac {t- tau} {c}} right) , dt}$
куда ${ displaystyle c}$ коэффициент масштабирования, ${ Displaystyle тау}$ представляет коэффициент временного сдвига
и, как уже упоминалось в этом контексте, вейвлет-преобразование соответствует свертке функции ${ Displaystyle у (т)}$ и вейвлет-функция. Свертка может быть реализована как умножение в частотной области. При этом следующий подход к реализации приводит к:
- Фурье-преобразование сигнала ${ Displaystyle у (к)}$ с БПФ
- Выбор дискретного масштабного коэффициента ${ displaystyle c_ {n}}$
- Масштабирование вейвлет-базисной функции по этому коэффициенту ${ displaystyle c_ {n}}$ и последующее БПФ этой функции
- Умножение на преобразованный сигнал YFFT первого шага
- Обратное преобразование продукта во временную область приводит к ${ Displaystyle Y_ {W} (с, тау)}$ для разных дискретных значений ${ Displaystyle тау}$ и дискретное значение ${ displaystyle c_ {n}}$
- Вернемся ко второму шагу, пока все дискретные значения масштабирования для ${ displaystyle c_ {n}}$ обрабатываются
Существует множество различных типов вейвлет-преобразований для конкретных целей. См. Также полный список преобразований, связанных с вейвлетами но наиболее распространенные из них перечислены ниже: Мексиканская шляпа вейвлет, Вейвлет Хаара, Вейвлет Добеши, треугольный вейвлет.