WikiDer > Ячейка Вигнера – Зейтца

Wigner–Seitz cell

В Ячейка Вигнера – Зейтца, названный в честь Юджин Вигнер и Фредерик Зейтц, это примитивная клетка который был построен путем применения Разложение Вороного к кристаллическая решетка. Он используется при изучении кристаллический материалы в физика твердого тела.

Примитивная ячейка Вигнера – Зейтца для решеток параллелограммов с разными углами.

Уникальное свойство кристалла состоит в том, что его атомы расположены в обычном трехмерном массиве, называемом решетка. Все свойства, приписываемые кристаллическим материалам, проистекают из этой высокоупорядоченной структуры. Такая структура демонстрирует дискретный поступательная симметрия. Чтобы смоделировать и изучить такую периодическую систему, нужна математическая «ручка» для описания симметрии и, следовательно, заключения о свойствах материала, вытекающих из этой симметрии. Ячейка Вигнера – Зейтца является средством достижения этого.

Ячейка Вигнера – Зейтца является примером примитивная клетка, который является ячейка содержащий ровно одну точку решетки. Для любой данной решетки существует бесконечное количество возможных примитивных ячеек. Однако для любой данной решетки существует только одна ячейка Вигнера – Зейтца. Это локус точек в пространстве, которые ближе к этой точке решетки, чем к любой из других точек решетки.

Клетка Вигнера – Зейтца, как и любая примитивная клетка, является фундаментальная область для дискретной трансляционной симметрии решетки. Первобытная ячейка обратная решетка в импульсное пространство называется Зона Бриллюэна.

Обзор

Фон

Концепция чего-либо разложение Вороного был исследован Питер Густав Лежен Дирихле, ведущий к имени Домен Дирихле. Дальнейшие взносы были внесены Евграф Федоров, (Федоровский параллелоэдр), Георгий Вороной (Многогранник Вороного),^[1]^[2] и Пол Ниггли (Wirkungsbereich).^[3]

Приложение к физика конденсированного состояния был впервые предложен Юджин Вигнер и Фредерик Зейтц в статье 1933 года, где он был использован для решения Уравнение Шредингера для свободных электронов в элементале натрий.^[4] Они аппроксимировали форму ячейки Вигнера-Зейтца в натрии, которая представляет собой усеченный октаэдр, как сферу равного объема и решили уравнение Шредингера точно, используя периодические граничные условия, которые требуют ${ displaystyle d psi / dr = 0}$ на поверхности сферы. Аналогичный расчет, который также учитывал несферический характер ячейки Вигнера-Зейтца, был выполнен позже Джон С. Слейтер.^[5]

Есть только пять топологически различных многогранников, которые мозаичны. трехмерное пространство, $ℝ 3$ . Они называются параллелоэдры. Они представляют математический интерес, например, в высших измерениях.^[6] Эти пять паралеллоэдров можно использовать для классификации трехмерных решеток с использованием концепции проективной плоскости, как это было предложено Джон Хортон Конвей и Нил Слоан.^[7] Однако в то время как топологическая классификация рассматривает любые аффинное преобразование чтобы привести к идентичному классу, более конкретная классификация приводит к 24 различным классам многогранников Вороного с параллельными краями, которые образуют плитку.^[3] Например, прямоугольный кубоид, правая квадратная призма, и куб принадлежат к одному топологическому классу, но отличаются разным соотношением сторон. Эта классификация 24 типов многогранников Вороного для решеток Бравэ была впервые предложена Борис Делоне.^[8]

Определение

Ячейка Вигнера – Зейтца вокруг точки решетки определяется как локус точек в пространстве, которые ближе к этой точке решетки, чем к любой из других точек решетки.^[9]

Математически можно показать, что ячейка Вигнера – Зейтца является примитивная клетка. Это означает, что ячейка охватывает весь прямое пространство не оставляя зазоров или отверстий, свойство, известное как мозаика.

Построение ячейки

Построение примитивной ячейки Вигнера – Зейтца.

Общая математическая концепция, воплощенная в ячейке Вигнера – Зейтца, чаще называется Ячейка Вороного, а разбиение плоскости на эти ячейки для данного набора точечных узлов известно как Диаграмма Вороного.

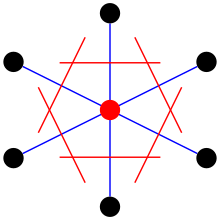
Процесс построения ячейки Вигнера-Зейтца гексагональной решетки.

Ячейку можно выбрать, предварительно выбрав точка решетки. После выбора точки ко всем ближайшим точкам решетки проводятся линии. В середине каждой линии проводится другая линия. нормальный к каждому из первого набора строк.

В случае трехмерной решетки перпендикулярная плоскость проводится в средней точке линий между точками решетки. При использовании этого метода наименьшая площадь (или объем) заключена таким образом и называется Примитивная ячейка Вигнера – Зейтца. Вся область (или пространство) внутри решетки будет заполнено примитивной ячейкой этого типа и не будет оставлять зазоров.

Соседние точки решетки непрерывно исследуются до тех пор, пока ограниченная площадь или объем не станет правильной площадью или объемом для примитивная клетка. В качестве альтернативы, если базисные векторы решетки сокращаются с использованием редукция решетки необходимо использовать только заданное количество точек решетки.^[10] В двух измерениях должны использоваться только точки решетки, которые составляют 4 элементарные ячейки, имеющие общую вершину с началом координат. В трехмерном пространстве необходимо использовать только те точки решетки, которые составляют 8 элементарных ячеек, имеющих общую вершину с началом координат.

Ячейка Вигнера-Зейтца примитивная кубическая решетка - это куб. В математике он известен как кубические соты.

Ячейка Вигнера – Зейтца объемно-центрированный кубический решетка - это усеченный октаэдр.^[9] В математике он известен как усеченные кубические соты.

Ячейка Вигнера – Зейтца гранецентрированная кубическая решетка - это ромбический додекаэдр.^[9] В математике он известен как ромбические додекаэдрические соты.

Ячейка Вигнера – Зейтца Телоцентрированный тетрагональный решетка, имеющая постоянные решетки с

{ displaystyle c / a> { sqrt {2}}}

это удлиненный додекаэдр.

Ячейка Вигнера – Зейтца примитивный шестиугольник решетка шестиугольная призма. В математике он известен как шестиугольные призматические соты.

Форма ячейки Вигнера-Зейтца для любой решетки Браве имеет форму одного из 24 многогранников Вороного.^[3]^[11] Чтобы указать дополнительные ограничения, ${ displaystyle a, b, c, alpha, beta}$ - параметры элементарной ячейки, а ${ displaystyle { vec {a}} _ {1}, { vec {a}} _ {2}, { vec {a}} _ {3}, { vec {a}} _ {4} }$ являются базисными векторами.
		Топологический класс (аффинный эквивалент параллелоэдр)
		Усеченный октаэдр	Удлиненный додекаэдр	Ромбический додекаэдр	Гексагональная призма	Куб
Решетка Браве	Примитивная кубическая					Любой
	Гранецентрированная кубическая			Любой
	Телоцентрированный кубический	Любой
	Примитивный шестиугольник				Любой
	Первобытный ромбоэдр	${ displaystyle alpha> 90}$ °		${ Displaystyle альфа <90}$ °
	Первобытный тетрагональный					Любой
	Телоцентрированный тетрагональный	${ displaystyle c / a <{ sqrt {2}}}$	${ displaystyle c / a> { sqrt {2}}}$
	Примитивный орторомбический					Любой
	Орторомбическая с центром в основании				Любой
	Орторомбическая гранецентрированная	Любой
	Телоцентрированный ромбический	${ displaystyle c ^ {2}$	${ displaystyle c ^ {2}> a ^ {2} + b ^ {2}}$	${ displaystyle c ^ {2} = a ^ {2} + b ^ {2}}$
	Примитивная моноклиника				Любой
	Базоцентрированная моноклиника	${ displaystyle a$	${ displaystyle a> b}$ , ${ displaystyle a ^ {2} -b ^ {2}> 2ac cos { beta}}$	${ displaystyle a> b}$ , ${ displaystyle a ^ {2} -b ^ {2} = 2ac cos { beta}}$
	Базоцентрированная моноклиника	${ displaystyle a> b}$ , ${ displaystyle a ^ {2} -b ^ {2} <2ac cos { beta}}$	${ displaystyle a = b}$
	Примитивная триклиника	${ displaystyle { vec {a}} _ {i} cdot { vec {a}} _ {j} neq 0}$ ${ displaystyle i, j in {1,2,3,4 }}$ куда ${ displaystyle i neq j}$	${ displaystyle { vec {a}} _ {i} cdot { vec {a}} _ {j} = 0}$ один раз	${ displaystyle { vec {a}} _ {i} cdot { vec {a}} _ {j} = 0 = { vec {a}} _ {k} cdot { vec {a}} _ {l}}$ ${ displaystyle i, j, k, l in {1,2,3,4 }}$ куда ${ Displaystyle я neq j neq k neq l}$

Композитные решетки

За композитные решетки, (кристаллы, имеющие более одного вектора в своем основа) каждая отдельная точка решетки представляет собой несколько атомов. Мы можем разбить каждую ячейку Вигнера – Зейтца на подъячейки путем дальнейшего разложения Вороного по ближайшему атому, а не по ближайшей точке решетки.^[12] Например, кристаллическая структура алмаза содержит двухатомный базис. В алмазе атомы углерода имеют тетрахеральный зр³ связь, но с тех пор тетраэдры не закрывают пространство, разложение Вороного кристаллической структуры алмаза на самом деле является усеченные четырехгранные соты triakis.^[13] Другой пример - применение разложения Вороного к атомам в Фазы A15, который формирует полиэдральная аппроксимация структуры Вира – Фелана.

Симметрия

Ячейка Вигнера – Зейтца всегда имеет одно и то же точечная симметрия в качестве основного Решетка Браве.^[9] Например, куб, усеченный октаэдр, и ромбический додекаэдр имеют точечную симметрию O_час, поскольку все соответствующие решетки Браве, использованные для их генерации, принадлежат кубической решетчатая система, который имеет O_час точечная симметрия.

Зона Бриллюэна

На практике сама ячейка Вигнера – Зейтца редко используется для описания прямое пространство, где обычный элементарные ячейки вместо них обычно используются. Однако такое же разложение чрезвычайно важно при применении к взаимное пространство. Ячейка Вигнера – Зейтца в обратном пространстве называется ячейкой Зона Бриллюэна, который содержит информацию о том, будет ли материал дирижер, полупроводник или изолятор.

Navigation

Navigation

Themenportale