WikiDer > Аэродинамика

Aerodynamics
«Аэродинамика» перенаправляется сюда. Для использования в других целях см. Аэродинамический (значения).
НАСА турбулентность в следе учиться в Остров Валлопс в 1990 году. вихрь создается пролетом крыла самолета, обнаруженного дымом. Вихри - одно из многих явлений, связанных с изучением аэродинамики.

Аэродинамика, из Греческий ἀήρ аэро (воздух) + δυναμική (динамика), это исследование движения воздуха, особенно при воздействии твердого предмета, такого как самолет крыло. Это подполе динамика жидкостей и газовая динамика, и многие аспекты теории аэродинамики являются общими для этих областей. Период, термин аэродинамика часто используется как синоним газовой динамики, с той разницей, что «газовая динамика» применяется к изучению движения всех газов и не ограничивается воздухом. Формальное изучение аэродинамики в современном понимании началось в восемнадцатом веке, хотя наблюдения фундаментальных концепций, таких как аэродинамическое сопротивление были записаны намного раньше. Большинство первых усилий в аэродинамике было направлено на достижение полет тяжелее воздуха, что впервые было продемонстрировано Отто Лилиенталь в 1891 г.[1] С тех пор использование аэродинамики за счет математический анализ, эмпирические приближения, аэродинамическая труба экспериментирование и компьютерное моделирование сформировал рациональную основу для развития полетов тяжелее воздуха и ряда других технологий. Недавние работы в области аэродинамики были сосредоточены на вопросах, связанных с сжимаемый поток, турбулентность, и пограничные слои и стал все больше вычислительный в природе.

История

Основная статья: История аэродинамики

Современная аэродинамика восходит только к семнадцатому веку, но люди тысячелетиями использовали аэродинамические силы в парусных лодках и ветряных мельницах,[2] и изображения и истории полета появляются на протяжении всей записанной истории,[3] такой как Древнегреческий легенда о Икар и Дедал.[4] Основные концепции континуум, тащить, и градиенты давления появляются в работе Аристотель и Архимед.[5]

В 1726 г. Сэр Исаак Ньютон стал первым, кто разработал теорию сопротивления воздуха,[6] сделав его одним из первых аэродинамиков. нидерландский язык-Швейцарский математик Даниэль Бернулли последовал в 1738 году с Гидродинамика в котором он описал фундаментальную взаимосвязь между давлением, плотностью и скоростью потока для несжимаемого потока, известного сегодня как Принцип Бернулли, который предоставляет один из методов расчета аэродинамической подъемной силы.[7] В 1757 г. Леонард Эйлер опубликовал более общий Уравнения Эйлера которое можно применить как к сжимаемым, так и к несжимаемым потокам. Уравнения Эйлера были расширены для включения эффектов вязкости в первой половине 1800-х годов, в результате чего Уравнения Навье – Стокса.[8][9] Уравнения Навье-Стокса являются наиболее общими определяющими уравнениями потока жидкости, но их трудно решить для обтекания любых форм, кроме самых простых.

Реплика Братья Райт' аэродинамическая труба выставлен в Центре авиации и космонавтики Вирджинии. Аэродинамические трубы сыграли ключевую роль в разработке и подтверждении законов аэродинамики.

В 1799 г. Сэр Джордж Кэли стал первым человеком, определившим четыре аэродинамические силы полета (масса, поднимать, тащить, и толкать), а также отношения между ними,[10][11] тем самым обозначив путь к достижению полетов тяжелее воздуха в следующем столетии. В 1871 г. Фрэнсис Герберт Уэнам построил первый аэродинамическая труба, позволяющий точно измерять аэродинамические силы. Теории перетаскивания были разработаны Жан ле Ронд д'Аламбер,[12] Густав Кирхгоф,[13] и Лорд Рэйли.[14] В 1889 г. Чарльз Ренар, французский авиационный инженер, стал первым человеком, который разумно предсказал мощность, необходимую для непрерывного полета.[15] Отто Лилиенталь, первый человек, добившийся большого успеха в полетах на планерах, был также первым, кто предложил тонкие изогнутые профили, обеспечивающие высокую подъемную силу и низкое лобовое сопротивление. Основываясь на этих разработках, а также на исследованиях, проведенных в их собственной аэродинамической трубе, компания Братья Райт совершил полет на первом самолете с двигателем 17 декабря 1903 года.

Во время первых полетов, Фредерик В. Ланчестер,[16] Мартин Кутта, и Николай Жуковский независимо созданные теории, которые связывают обращение потока жидкости для подъема. Кутта и Жуковский разработали двумерную теорию крыла. Продолжая работу Ланчестера, Людвиг Прандтль приписывают развитие математики[17] за теорию тонкого профиля и подъемной линии, а также работу с пограничные слои.

По мере увеличения скорости самолетов конструкторы начали сталкиваться с проблемами, связанными с воздухом. сжимаемость на скоростях, близких к скорости звука или превышающих их. Различия в воздушных потоках в таких условиях приводят к проблемам в управлении самолетом, повышенному сопротивлению из-за ударные волны, и угроза разрушения конструкции из-за аэроупругий флаттер. Отношение скорости потока к скорости звука было названо число Маха после Эрнст Мах кто одним из первых исследовал свойства сверхзвуковой поток. Маккорн Ренкин и Пьер Анри Гюгонио независимо разработал теорию свойств текучести до и после ударная волна, пока Якоб Акерет провел начальную работу по расчету подъемной силы и сопротивления сверхзвуковых профилей.[18] Теодор фон Карман и Хью Латимер Драйден ввел термин трансзвуковой для описания скорости потока около 1 Маха, когда сопротивление быстро увеличивается. Это быстрое увеличение сопротивления привело к тому, что аэродинамики и авиаторы не пришли к единому мнению о возможности сверхзвукового полета до тех пор, пока звуковой барьер был впервые сломан в 1947 году с помощью Колокол X-1 самолет.

К тому времени, как звуковой барьер был преодолен, понимание аэродинамиками дозвукового и слабого сверхзвукового потока сформировалось. В Холодная война подтолкнула к созданию постоянно развивающейся линейки высокопроизводительных самолетов. Вычислительная гидродинамика началась как попытка найти свойства обтекания сложных объектов и быстро выросла до точки, когда весь самолет может быть спроектирован с использованием компьютерного программного обеспечения, с испытаниями в аэродинамической трубе, за которыми следуют летные испытания для подтверждения компьютерных прогнозов. Понимание сверхзвуковой и гиперзвуковой Аэродинамика достигла зрелости с 1960-х годов, и цели аэродинамиков сместились с поведения потока жидкости на проектирование транспортного средства, которое предсказуемо взаимодействует с потоком жидкости. Конструирование самолетов для сверхзвуковых и гиперзвуковых условий, а также стремление улучшить аэродинамическую эффективность существующих самолетов и силовых установок продолжает мотивировать новые исследования в области аэродинамики, в то время как работа по важным проблемам базовой аэродинамической теории, связанным с турбулентностью потока, продолжается. существование и единственность аналитических решений уравнений Навье-Стокса.

Основные концепции

Силы бегства на профиль

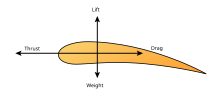
Понимание движения воздуха вокруг объекта (часто называемого полем потока) позволяет рассчитать силы и моменты воздействуя на объект. Во многих задачах аэродинамики интересующие силы являются фундаментальными силами полета: поднимать, тащить, толкать, и масса. Из них подъемная сила и сопротивление - это аэродинамические силы, то есть силы, возникающие при обтекании твердым телом воздуха. Расчет этих величин часто основан на предположении, что поле течения ведет себя как континуум. Поля сплошного течения характеризуются такими свойствами, как скорость потока, давление, плотность, и температура, которые могут быть функциями положения и времени. Эти свойства могут быть прямо или косвенно измерены в аэродинамических экспериментах или рассчитаны, исходя из уравнений сохранения массы, импульс, и энергия в воздушных потоках. Плотность, скорость потока и дополнительное свойство, вязкость, используются для классификации полей потока.

Классификация потока

Скорость потока используется для классификации потоков по скоростному режиму. Дозвуковые потоки - это поля течения, в которых поле скорости воздуха всегда ниже местной скорости звука. Трансзвуковые потоки включают в себя как области дозвукового потока, так и области, в которых локальная скорость потока больше, чем локальная скорость звука. Сверхзвуковые потоки определяются как потоки, в которых скорость потока везде больше скорости звука. Четвертая классификация, гиперзвуковой поток, относится к потокам, в которых скорость потока намного превышает скорость звука. Аэродинамики расходятся во мнениях относительно точного определения гиперзвукового потока.

Сжимаемый поток учитывает различную плотность в потоке. Дозвуковые потоки часто идеализируются как несжимаемые, т.е. плотность считается постоянной. Трансзвуковые и сверхзвуковые потоки сжимаемы, и расчеты, не учитывающие изменения плотности в этих полях течения, дадут неточные результаты.

Вязкость связана с силами трения в потоке. В некоторых полях течения вязкие эффекты очень малы, и в приближенных решениях вязкими эффектами можно пренебречь. Эти приближения называются невязкими потоками. Течения, для которых не пренебрегают вязкостью, называются вязкими потоками. Наконец, аэродинамические проблемы также могут быть классифицированы по среде потока. Внешняя аэродинамика - это изучение обтекания твердых объектов различной формы (например, вокруг крыла самолета), в то время как внутренняя аэродинамика - это исследование обтекания каналов внутри твердых объектов (например, через реактивный двигатель).

Предположение о континууме

В отличие от жидкостей и твердых тел, газы состоят из дискретных молекулы которые занимают лишь небольшую часть объема, заполненного газом. На молекулярном уровне поля течения состоят из столкновений множества отдельных молекул газа между собой и с твердыми поверхностями. Однако в большинстве аэродинамических приложений дискретная молекулярная природа газов не учитывается, и предполагается, что поле потока ведет себя как континуум. Это предположение позволяет определять свойства жидкости, такие как плотность и скорость потока, везде в пределах потока.

Срок действия предположение континуума зависит от плотности газа и рассматриваемого применения. Для верности предположения о континууме длина свободного пробега длина должна быть намного меньше, чем масштаб рассматриваемого приложения. Например, многие приложения в области аэродинамики имеют дело с самолетами, летящими в атмосферных условиях, когда длина свободного пробега составляет порядка микрометров, а тело на несколько порядков больше. В этих случаях масштаб длины летательного аппарата составляет от нескольких метров до нескольких десятков метров, что намного больше, чем длина среднего свободного пробега. Для таких приложений разумно предположение о континууме. Предположение о континууме менее справедливо для потоков с крайне низкой плотностью, например, с которыми сталкиваются транспортные средства на очень больших высотах (например, 300000 футов / 90 км).[5] или спутники в Низкая околоземная орбита. В таких случаях статистическая механика является более точным методом решения проблемы, чем сплошная аэродинамика. В Число Кнудсена может использоваться для выбора между статистической механикой и непрерывной формулировкой аэродинамики.

Законы сохранения

Предположение о жидкий континуум позволяет решать проблемы аэродинамики с помощью законы сохранения гидродинамики. Используются три принципа сохранения:

Сохранение массы
Сохранение массы требует, чтобы масса не создавалась и не разрушалась в потоке; математическая формулировка этого принципа известна как уравнение неразрывности.
Сохранение импульса
Математическую формулировку этого принципа можно рассматривать как приложение Второй закон Ньютона. Импульс внутри потока изменяется только внешними силами, которые могут включать в себя как поверхностные силы, например вязкий (фрикционный) силы, и силы тела, Такие как масса. Принцип сохранения импульса может быть выражен как вектор уравнение или разделить на набор из трех скаляр уравнения (x, y, z компоненты).
Сохранение энергии
Уравнение сохранения энергии утверждает, что энергия не создается и не разрушается в потоке, и что любое добавление или вычитание энергии к объему в потоке вызвано: теплопередача, или работай в и из интересующей области.

Вместе эти уравнения известны как Уравнения Навье-Стокса, хотя некоторые авторы определяют термин, чтобы включить только уравнение (а) импульса. Уравнения Навье-Стокса не имеют известного аналитического решения и решаются в современной аэродинамике с использованием вычислительные методы. Поскольку вычислительные методы с использованием высокоскоростных компьютеров исторически не были доступны и высокая вычислительная стоимость решения этих сложных уравнений теперь, когда они доступны, упрощения уравнений Навье-Стокса применялись и продолжают использоваться. В Уравнения Эйлера представляют собой набор аналогичных уравнений сохранения, которые не учитывают вязкость, и могут использоваться в случаях, когда ожидается, что влияние вязкости будет небольшим. Дальнейшие упрощения приводят к Уравнение Лапласа и потенциальный поток теория. Кроме того, Уравнение Бернулли является решением в одном измерении уравнений сохранения импульса и энергии.

В закон идеального газа или другой такой уравнение состояния часто используется в сочетании с этими уравнениями для формирования определенной системы, которая позволяет найти решение для неизвестных переменных.[19]

Отрасли аэродинамики

вычислительное моделирование

Аэродинамические проблемы классифицируются по среде потока или свойствам потока, включая скорость потока, сжимаемость, и вязкость. Внешний аэродинамика - это исследование обтекания твердых предметов различной формы. Оценка поднимать и тащить на самолет или ударные волны образуют перед носом ракета являются примерами внешней аэродинамики. Внутренний аэродинамика - это исследование обтекания твердых тел. Например, внутренняя аэродинамика включает в себя исследование воздушного потока через реактивный двигатель или через кондиционер трубка.

Аэродинамические проблемы также можно классифицировать в зависимости от того, скорость потока ниже, рядом или выше скорость звука. Проблема называется дозвуковой, если все скорости в задаче меньше скорости звука. трансзвуковой если присутствуют скорости как ниже, так и выше скорости звука (обычно, когда характерная скорость приблизительно равна скорости звука), сверхзвуковой когда характерная скорость потока больше скорости звука, и гиперзвуковой когда скорость потока намного больше скорости звука. Аэродинамики расходятся во мнениях относительно точного определения гиперзвукового потока; грубое определение рассматривает потоки с Числа Маха выше 5 - гиперзвуковой.[5]

Влияние вязкость по потоку диктует третья классификация. Некоторые проблемы могут иметь очень малые вязкостные эффекты, и в этом случае вязкость можно считать незначительной. Приближения к этим задачам называются невязкие потоки. Течения, в которых нельзя пренебрегать вязкостью, называются вязкими потоками.

Несжимаемая аэродинамика

Дальнейшая информация: несжимаемый поток

Несжимаемый поток - это поток, плотность которого постоянна как во времени, так и в пространстве. Хотя все реальные жидкости являются сжимаемыми, поток часто считается несжимаемым, если эффект изменения плотности вызывает лишь небольшие изменения в расчетных результатах. Это более вероятно, если скорость потока значительно ниже скорости звука. Эффекты сжимаемости более значительны при скоростях, близких к скорости звука или превышающих их. В число Маха используется для оценки того, можно ли предположить несжимаемость, в противном случае необходимо учитывать влияние сжимаемости.

Дозвуковой поток

Дозвуковая (или низкоскоростная) аэродинамика описывает движение жидкости в потоках, которые намного ниже скорости звука повсюду в потоке. Есть несколько ветвей дозвукового течения, но один частный случай возникает, когда течение невязкий, несжимаемый и безвихревый. Этот случай называется потенциальный поток и позволяет дифференциальные уравнения которые описывают поток как упрощенную версию уравнений динамика жидкостей, тем самым предоставляя аэродинамику ряд быстрых и простых решений.[20]

При решении дозвуковой задачи аэродинамик должен принять одно решение - учитывать ли эффекты сжимаемости. Сжимаемость - это описание степени изменения плотность в потоке. Когда влияние сжимаемости на раствор невелико, можно сделать предположение, что плотность постоянна. Тогда проблема заключается в несжимаемой задаче аэродинамики на малых скоростях. Когда плотность может изменяться, поток называют сжимаемым. В воздухе эффекты сжимаемости обычно игнорируются, когда число Маха в потоке не превышает 0,3 (около 335 футов (102 м) в секунду или 228 миль (366 км) в час при 60 ° F (16 ° C)). При скорости выше 0,3 Маха проблемный поток следует описывать с помощью сжимаемой аэродинамики.

Сжимаемая аэродинамика

Основная статья: Сжимаемый поток

Согласно теории аэродинамики, поток считается сжимаемым, если плотность меняется вдоль рационализировать. Это означает, что в отличие от потока несжимаемой жидкости учитываются изменения плотности. В общем, это тот случай, когда число Маха поток частично или полностью превышает 0,3. Значение Маха 0,3 довольно условно, но оно используется потому, что потоки газа с числом Маха ниже этого значения демонстрируют изменения плотности менее 5%. Кроме того, максимальное изменение плотности на 5% происходит на точка застоя (точка на объекте, где скорость потока равна нулю), а плотность изменения вокруг остальной части объекта будет значительно ниже. Трансзвуковые, сверхзвуковые и гиперзвуковые потоки являются сжимаемыми потоками.

Трансзвуковой поток

Основная статья: Трансзвуковой

Термин Transonic относится к диапазону скоростей потока чуть ниже и выше местного значения. скорость звука (обычно принимается как Мах 0,8–1,2). Он определяется как диапазон скоростей между критическое число Маха, когда некоторые части воздушного потока над самолетом становятся сверхзвуковой, и более высокая скорость, обычно около 1,2 Маха, когда весь воздушный поток сверхзвуковой. Между этими скоростями часть воздушного потока является сверхзвуковой, а часть воздушного потока - несверхзвуковой.

Сверхзвуковой поток

Основная статья: Сверхзвуковой

Сверхзвуковые аэродинамические проблемы связаны со скоростью потока, превышающей скорость звука. Расчет подъемной силы на Конкорд во время крейсерского полета может быть примером сверхзвуковой аэродинамической задачи.

Сверхзвуковой поток ведет себя совсем не так, как дозвуковой. Жидкости реагируют на перепады давления; изменения давления - это то, как жидкости «приказывают» реагировать на окружающую среду. Следовательно, поскольку звук фактически является бесконечно малым перепадом давления, распространяющимся через жидкость, скорость звука в этой жидкости может считаться самой быстрой скоростью, с которой «информация» может перемещаться в потоке. Наиболее очевидно это различие проявляется в случае удара жидкости о объект. Перед этим объектом жидкость образует давление застоя поскольку столкновение с объектом останавливает движущуюся жидкость. В жидкости, движущейся с дозвуковой скоростью, это возмущение давления может распространяться вверх по потоку, изменяя структуру потока перед объектом и создавая впечатление, что жидкость «знает», что объект находится там, по-видимому, регулируя его движение и обтекая его. Однако в сверхзвуковом потоке возмущение давления не может распространяться вверх по потоку. Таким образом, когда жидкость, наконец, достигает объекта, она ударяется о нем, и жидкость вынуждена изменить свои свойства - температура, плотность, давление, и число Маха- в чрезвычайно жестоком и необратимый мода называется ударная волна. Наличие ударных волн, наряду с эффектами сжимаемости высокой скорости потока (см. Число Рейнольдса) жидкости, является центральным отличием сверхзвукового и дозвукового режимов аэродинамики.

Гиперзвуковой поток

Основная статья: Гиперзвуковой

В аэродинамике гиперзвуковые скорости - это сверхзвуковые скорости. В 1970-е годы этот термин обычно относился к скорости 5 Маха (в 5 раз больше скорости звука) и выше. Гиперзвуковой режим является подмножеством сверхзвукового режима. Гиперзвуковое течение характеризуется высокотемпературным течением за ударной волной, вязким взаимодействием и химической диссоциацией газа.

Связанная терминология

Различные типы анализа обтекания профиля:
  Потенциальный поток теория
  Течение пограничного слоя теория
  Бурный след анализ

Режимы потока несжимаемой и сжимаемой жидкости вызывают множество связанных явлений, таких как пограничные слои и турбулентность.

Пограничные слои

Основная статья: Пограничный слой

Концепция пограничный слой важен во многих задачах аэродинамики. Вязкость и трение жидкости в воздухе оцениваются как существенные только в этом тонком слое. Это предположение делает описание такой аэродинамики более податливым математически.

Турбулентность

Основная статья: Турбулентность

В аэродинамике турбулентность характеризуется хаотическим изменением свойств потока. К ним относятся диффузия с низким импульсом, конвекция с высоким импульсом и быстрое изменение давления и скорости потока в пространстве и времени. Нетурбулентный поток называется ламинарный поток.

Аэродинамика в других областях

Инженерный дизайн

Дальнейшая информация: Автомобильная аэродинамика

Аэродинамика - важный элемент конструкция автомобиля, включая дорожные автомобили и грузовики где основная цель - уменьшить транспортное средство коэффициент трения, и гоночные автомобили, где помимо уменьшения лобового сопротивления целью является также повышение общего уровня прижимная сила.[20] Аэродинамика также важна для прогнозирования сил и моментов, действующих на парусные суда. Он используется в конструкции механических компонентов, таких как жесткий диск головы. Строительные инженеры прибегают к аэродинамике, и особенно аэроупругость, при расчете ветер нагрузки при проектировании больших зданий, мосты, и Ветряные турбины

Аэродинамика внутренних проходов важна в отопление / вентиляция, газопровод, И в автомобильные двигатели где подробные схемы потока сильно влияют на производительность двигателя.

Экологический дизайн

Городская аэродинамика изучается градостроители и дизайнеры, стремящиеся улучшить удобства в открытых пространствах или при создании городского микроклимата для уменьшения воздействия городского загрязнения. Область экологической аэродинамики описывает способы, которыми атмосферная циркуляция а механика полета влияет на экосистемы.

Аэродинамические уравнения используются в численный прогноз погоды.

Контроль мяча в спорте

Виды спорта, в которых решающее значение имеет аэродинамика, включают: футбольный, настольный теннис, крикет, бейсбол, и гольф, в котором опытные игроки могут контролировать траекторию мяча с помощью кнопки "Эффект Магнуса".

Смотрите также

Рекомендации

  1. ^ "Как аист вдохновил человека на полет". flyingmag.com.[постоянная мертвая ссылка]
  2. ^ «Истоки ветроэнергетики (1000 г. до н.э. - 1300 г. н.э.) Иллюстрированная история развития ветроэнергетики». Telosnet.com.
  3. ^ Берлинер, Дон (1997). Авиация: стремясь к небу. Оливер Пресс, Inc. стр. 128. ISBN 1-881508-33-1.
  4. ^ Овидий; Грегори, Х. (2001). Метаморфозы. Печатка Классика. ISBN 0-451-52793-3. OCLC 45393471.
  5. ^ а б c Андерсон, Джон Дэвид (1997). История аэродинамики и ее влияние на летательные аппараты. Нью-Йорк, Нью-Йорк: Издательство Кембриджского университета. ISBN 0-521-45435-2.
  6. ^ Ньютон, И. (1726). Philosophiae Naturalis Principia Mathematica, Книга II.
  7. ^ «Гидродинамика». Британская онлайн-энциклопедия. Получено 2008-10-30.
  8. ^ Навье, К. Л. М. Х. (1827). "Memoire sur les lois du mouvement des fluides". Mémoires de l'Académie des Sciences. 6: 389–440.
  9. ^ Стокс, Г. (1845). «К теории внутреннего трения движущихся жидкостей». Труды Кембриджского философского общества. 8: 287–305.
  10. ^ "Столетие комиссии США по полетам - сэр Джордж Кейли". Архивировано из оригинал 20 сентября 2008 г.. Получено 2008-09-10. Сэра Джорджа Кэли, родившегося в 1773 году, иногда называют отцом авиации. Пионер в своей области, он первым определил четыре аэродинамические силы полета - вес, подъемную силу, сопротивление и тягу, а также их взаимосвязь. Он также был первым, кто построил успешный планер для перевозки людей. Кэли описал многие концепции и элементы современного самолета и был первым, кто понял и объяснил с технической точки зрения концепции подъемной силы и тяги.
  11. ^ Кэли, Джордж. «О воздушной навигации» Часть 1 В архиве 2013-05-11 в Wayback Machine, Часть 2 В архиве 2013-05-11 в Wayback Machine, Часть 3 В архиве 2013-05-11 в Wayback Machine Журнал естественной философии Николсона, 1809–1810. (Через НАСА). Необработанный текст. Дата обращения: 30 мая 2010.
  12. ^ Даламбер Дж. (1752 г.). Essai d'une Nouvelle Theorie de la Resistance des Fluides.
  13. ^ Кирхгоф, Г. (1869). "Zur Theorie freier Flussigkeitsstrahlen". Журнал für die reine und angewandte Mathematik. 1869 (70): 289–298. Дои:10.1515 / crll.1869.70.289. S2CID 120541431.
  14. ^ Рэлей, лорд (1876 г.). «О сопротивлении жидкостей». Философский журнал. 2 (13): 430–441. Дои:10.1080/14786447608639132.
  15. ^ Ренар, К. (1889). "Nouvelles испытывает сюр-ла-сопротивление воздуха". L'Aéronaute. 22: 73–81.
  16. ^ Ланчестер, Ф. У. (1907). Аэродинамика.
  17. ^ Прандтль, Л. (1919). Tragflügeltheorie. Göttinger Nachrichten, Mathematischphysikalische Klasse, 451–477.
  18. ^ Акерет Дж. (1925). "Luftkrafte auf Flugel, die mit der grosserer als Schallgeschwindigkeit bewegt werden". Zeitschrift für Flugtechnik und Motorluftschiffahrt. 16: 72–74.
  19. ^ «Понимание аэродинамики: рассуждения на основе реальной физики» Дуг Маклин, Джон Уайли и сыновья, 2012 Глава 3.2 «Основные соотношения, составляющие уравнения НС, - это основные законы сохранения массы, импульса и энергии. Чтобы иметь полный набор уравнений, нам также потребуется уравнение состояния, связывающее температуру, давление и плотность ... " https://play.google.com/books/reader?id=_DJuEgpmdr8C&printsec=frontcover&source=gbs_vpt_reviews&pg=GBS.PA191.w.0.0.0.151
  20. ^ а б Кац, Джозеф (1991). Низкоскоростная аэродинамика: от теории крыла к панельным методам. Серия McGraw-Hill в авиационной и аэрокосмической технике. Нью-Йорк: Макгроу-Хилл. ISBN 0-07-050446-6. OCLC 21593499.

дальнейшее чтение

Общая аэродинамика

Дозвуковая аэродинамика

Трансзвуковая аэродинамика

Сверхзвуковая аэродинамика

Гиперзвуковая аэродинамика

История аэродинамики

Аэродинамика, связанная с инженерией

Наземная техника

Самолет

Вертолеты

  • Лейшман, Дж. Гордон (2006). Принципы аэродинамики вертолета (2-е изд.). Издательство Кембриджского университета. ISBN 0-521-85860-7. OCLC 224565656.
  • Прути, Раймонд В. (2001). Характеристики, устойчивость и управляемость вертолета. Издательство Krieger Publishing Company Press. ISBN 1-57524-209-5. OCLC 212379050.
  • Seddon, J .; Ньюман, Саймон (2001). Базовая аэродинамика вертолета: изложение первых принципов гидромеханики и динамики полета однороторного вертолета. AIAA. ISBN 1-56347-510-3. OCLC 47623950.

Ракеты

Модель самолета

  • Саймонс, Мартин (1999). Модель аэродинамики самолета (4-е изд.). Trans-Atlantic Publications, Inc. ISBN 1-85486-190-5. OCLC 43634314.

Связанные разделы аэродинамики

Аэротермодинамика

Аэроупругость

  • Bisplinghoff, Raymond L .; Эшли, Холт; Halfman, Роберт Л. (1996). Аэроупругость. Dover Publications. ISBN 0-486-69189-6. OCLC 34284560.
  • Фунг, Ю. К. (2002). Введение в теорию аэроупругости. (Под ред. Феникса). Dover Publications. ISBN 0-486-49505-1. OCLC 55087733.

Пограничные слои

Турбулентность

внешняя ссылка