WikiDer > Алгоритмический вывод - Википедия

Алгоритмический вывод собирает новые разработки в статистические выводы методы, которые стали возможными благодаря мощным вычислительным устройствам, широко доступным любому аналитику данных. Краеугольными камнями в этой области являются теория вычислительного обучения, гранулярные вычисления, биоинформатика, и уже давно структурная вероятность (Фрейзер 1966Основное внимание уделяется алгоритмам, которые вычисляют статистику, основанную на изучении случайного явления, а также объем данных, которые они должны использовать для получения надежных результатов. Это отвлекает математиков от изучения законы распределения к функциональным свойствам статистика, а интерес компьютерных ученых от алгоритмов обработки данных к Информация они обрабатывают.

Проблема параметрического вывода Фишера

Относительно определения параметров закона распределения зрелый читатель может вспомнить длительные споры середины 20 века об интерпретации их изменчивости с точки зрения фидуциальное распределение (Фишер 1956), структурные вероятности (Фрейзер 1966), priors / posteriors (Рэмси 1925), и так далее. Из эпистемология точки зрения, это повлекло за собой сопутствующий спор о природе вероятность: можно ли описать физическую особенность явлений через случайные переменные или способ обобщения данных о явлении? Выбирая последнее, Фишер определяет реперное распределение закон параметров данной случайной величины, который он выводит из выборки ее спецификаций. С помощью этого закона он вычисляет, например, «вероятность того, что μ (среднее значение Гауссова переменная - наше примечание) меньше любого приписанного значения или вероятности того, что оно находится между любыми приписанными значениями, или, короче говоря, его распределения вероятностей в свете наблюдаемой выборки ».

Классическое решение

Фишер упорно боролся, чтобы защитить разницу и превосходство его представления о распределении параметров по сравнению с аналогичными понятиями, такими как Байеса апостериорное распределение, Конструктивная вероятность Фрейзера и теория Неймана доверительные интервалы. В течение полувека доверительные интервалы Неймана преобладали во всех практических целях, учитывая феноменологическую природу вероятности. С этой точки зрения, когда вы имеете дело с гауссовой переменной, ее среднее значение μ фиксируется физическими особенностями наблюдаемого вами явления, где наблюдения являются случайными операторами, следовательно, наблюдаемые значения являются характеристиками случайный пример. Из-за их случайности вы можете вычислить из выборки конкретных интервалов, содержащих фиксированный μ, с заданной вероятностью, которую вы обозначаете уверенность.

Пример

Позволять Икс быть гауссовой переменной^[1] с параметрами ${ displaystyle mu}$ и ${ displaystyle sigma ^ {2}}$ и ${ Displaystyle {X_ {1}, ldots, X_ {m} }}$ образец взят из него. Работа со статистикой

${ Displaystyle S _ { mu} = сумма _ {я = 1} ^ {м} X_ {я}}$

и

${ displaystyle S _ { sigma ^ {2}} = sum _ {i = 1} ^ {m} (X_ {i} - { overline {X}}) ^ {2}, { text {где} } { overline {X}} = { frac {S _ { mu}} {m}}}$

является выборочным средним, мы признаем, что

${ displaystyle T = { frac {S _ { mu} -m mu} { sqrt {S _ { sigma ^ {2}}}}} { sqrt { frac {m-1} {m}} } = { frac {{ overline {X}} - mu} { sqrt {S _ { sigma ^ {2}} / (м (м-1))}}}}$

следует за Распределение Стьюдента (Уилкс 1962) с параметром (степенями свободы) м - 1, так что

${ displaystyle f_ {T} (t) = { frac { Gamma (m / 2)} { Gamma ((m-1) / 2)}} { frac {1} { sqrt { pi ( m-1)}}} left (1 + { frac {t ^ {2}} {m-1}} right) ^ {m / 2}.}$

Измерение Т между двумя квантилями и инвертирование его выражения как функции ${ displaystyle mu}$ вы получаете доверительные интервалы для ${ displaystyle mu}$.

С образцом спецификации:

${ displaystyle mathbf {x} = {7.14,6.3,3.9,6.46,0.2,2.94,4.14,4.69,6.02,1.58 }}$

имеющий размер м = 10, вы вычисляете статистику ${ displaystyle s _ { mu} = 43,37}$ и ${ displaystyle s _ { sigma ^ {2}} = 46,07}$, и получить доверительный интервал 0,90 для ${ displaystyle mu}$ с крайностями (3,03, 5,65).

Вывод функций с помощью компьютера

С точки зрения моделирования весь спор выглядит как дилемма курица-яйцо: либо фиксированные данные первыми и вероятностное распределение их свойств как следствие, либо фиксированные свойства первыми и распределение вероятностей наблюдаемых данных как следствие. одно преимущество и один недостаток. Первое особенно ценилось еще тогда, когда люди еще выполняли вычисления с помощью листа и карандаша. По сути, задача вычисления доверительного интервала Неймана для фиксированного параметра θ является сложной: вы не знаете θ, но вы ищите возможность расположить вокруг него интервал с, возможно, очень низкой вероятностью неудачи. Аналитическое решение разрешено для очень ограниченного числа теоретических случаев. Наоборот большое количество случаев можно быстро решить в приблизительный способ через Центральная предельная теорема с точки зрения доверительного интервала вокруг гауссова распределения - это преимущество. Недостатком является то, что центральная предельная теорема применима, когда размер выборки достаточно велик. Следовательно, это все менее и менее применимо к образцу, используемому в современных случаях вывода. Ошибка не в размере выборки как таковой. Скорее, этот размер недостаточно велик из-за сложность проблемы вывода.

Благодаря наличию крупных вычислительных мощностей, ученые переориентировались с вывода изолированных параметров на вывод сложных функций, то есть наборов сильно вложенных параметров, идентифицирующих функции. В этих случаях мы говорим о изучение функций (например, с точки зрения регресс, нейронечеткая система или же вычислительное обучение) на основе высокоинформативных образцов. Первым следствием наличия сложной структуры, связывающей данные, является сокращение количества выборок. степени свободы, то есть сжигание части точек выборки, так что эффективный размер выборки, который следует учитывать в центральной предельной теореме, слишком мал. Сосредоточение внимания на размере выборки обеспечивает ограниченную ошибку обучения с заданным уровень уверенности, как следствие, нижняя граница этого размера растет с увеличением показатели сложности Такие как Размер ВК или же деталь класса которой принадлежит функция, которую мы хотим изучить.

Пример

Выборки из 1000 независимых битов достаточно, чтобы гарантировать абсолютную ошибку не более 0,081 при оценке параметра. п базовой переменной Бернулли с достоверностью не менее 0,99. Один и тот же размер не может гарантировать пороговое значение менее 0,088 с такой же достоверностью 0,99, когда ошибка определяется с вероятностью того, что 20-летний мужчина, живущий в Нью-Йорке, не соответствует диапазонам роста, веса и талии, наблюдаемым на 1000 Big Обитатели яблони. Недостаток точности возникает из-за того, что как размерность ВК, так и детализация класса параллелепипедов, среди которых попадает наблюдаемый из диапазонов 1000 жителей, равны 6.

Общая проблема обращения, решающая вопрос Фишера

При недостаточно больших выборках подход: фиксированная выборка - случайные свойства предлагает процедуры вывода в три этапа:

1.	Механизм отбора проб. Он состоит из пары ${ displaystyle (Z, g _ { boldsymbol { theta}})}$, где семя Z - случайная величина без неизвестных параметров, а объясняющая функция ${ displaystyle g _ { boldsymbol { theta}}}$ отображение функций из образцов Z к выборкам случайной величины Икс нас интересует. Вектор параметров ${ displaystyle { boldsymbol { theta}}}$ является спецификацией случайного параметра ${ Displaystyle mathbf { Theta}}$. Его составляющими являются параметры Икс закон распределения. Теорема интегрального преобразования гарантирует существование такого механизма для каждого (скалярного или векторного) Икс когда семя совпадает со случайной величиной U равномерно распространяется в ${ displaystyle [0,1]}$. Пример. За Икс после Распределение Парето с параметрами а и k, т.е. ${ displaystyle F_ {X} (x) = left (1 - { frac {k} {x}} ^ {a} right) I _ {[k, infty)} (x),}$ механизм отбора проб ${ Displaystyle (U, г _ {(а, к)})}$ за Икс с семенами U читает: ${ Displaystyle г _ {(а, к)} (и) = к (1-и) ^ {- { гидроразрыва {1} {а}}},}$ или, что то же самое, ${ displaystyle g _ {(a, k)} (u) = ku ^ {- 1 / a}.}$
2.	Основные уравнения. Фактическая связь между моделью и наблюдаемыми данными выражается в виде набора отношений между статистикой по данным и неизвестными параметрами, которые являются следствием механизмов выборки. Мы называем эти отношения основные уравнения. Вращение вокруг статистики ${ displaystyle s = h (x_ {1}, ldots, x_ {m}) = h (g _ { boldsymbol { theta}} (z_ {1}), ldots, g _ { boldsymbol { theta} } (z_ {m}))}$, общая форма главного уравнения: ${ displaystyle s = rho ({ boldsymbol { theta}}; z_ {1}, ldots, z_ {m})}$. С помощью этих соотношений мы можем проверить значения параметров, которые могли бы сгенерировать выборку с наблюдаемой статистикой из конкретной настройки начальных значений, представляющих начальное значение выборки. Следовательно, совокупности образцов семян соответствует совокупность параметров. Чтобы гарантировать чистоту свойств этой популяции, достаточно случайным образом нарисовать начальные значения и задействовать либо достаточная статистика или просто хорошая статистика w.r.t. параметры в основных уравнениях. Например, статистика ${ displaystyle s_ {1} = sum _ {i = 1} ^ {m} log x_ {i}}$ и ${ displaystyle s_ {2} = min _ {я = 1, ldots, m} {x_ {i} }}$ оказывается достаточно для параметров а и k случайной величины Парето Икс. Благодаря (эквивалентной форме) механизму отбора проб ${ Displaystyle г _ {(а, к)}}$ мы можем читать их как ${ displaystyle s_ {1} = m log k + 1 / a sum _ {i = 1} ^ {m} log u_ {i}}$ ${ displaystyle s_ {2} = min _ {i = 1, ldots, m} {ku_ {i} ^ {- { frac {1} {a}}} },}$ соответственно.
3.	Популяция параметра. Установив набор основных уравнений, вы можете сопоставить исходные данные образца с параметрами либо численно с помощью бутстрап населения, или аналитически через извилистый аргумент. Следовательно, из популяции семян вы получаете совокупность параметров. Пример. Из приведенного выше основного уравнения мы можем нарисовать пару параметров, ${ Displaystyle (а, к)}$, совместимый с наблюдаемым образцом, решив следующую систему уравнений: ${ displaystyle a = { frac { sum log u_ {i} -m log min {u_ {i} }} {s_ {1} -m log s_ {2}}}.}$ ${ displaystyle к = mathrm {e} ^ { frac {as_ {1} - sum log u_ {i}} {ma}}}$ куда ${ displaystyle s_ {1}}$ и ${ displaystyle s_ {2}}$ наблюдаемая статистика и ${ displaystyle u_ {1}, ldots, u_ {m}}$ набор однородных семян. Перенося в параметры вероятность (плотность) воздействия на семена, получаем закон распределения случайных параметров А и K совместимы с наблюдаемой вами статистикой. Совместимость обозначает параметры совместимых популяций, то есть популяций, которые мог бы создать образец, дающий начало наблюдаемой статистике. Вы можете формализовать это понятие следующим образом:

Определение

Для случайной величины и взятой из нее выборки совместимое распределение это распределение, имеющее такой же механизм отбора проб ${ displaystyle { mathcal {M}} _ {X} = (Z, g _ { boldsymbol { theta}})}$ из Икс со значением ${ displaystyle { boldsymbol { theta}}}$ случайного параметра ${ Displaystyle mathbf { Theta}}$ получено из основного уравнения, основанного на статистике правильного поведения s.

Пример

Совместная эмпирическая кумулятивная функция распределения параметров ${ Displaystyle (А, К)}$ случайной величины Парето.

Кумулятивная функция распределения среднего M гауссовой случайной величины

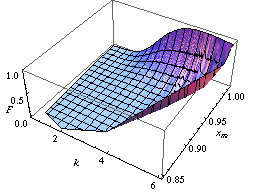
Вы можете найти закон распределения параметров Парето А и K как пример реализации бутстрап населения метод, как на рисунке слева.

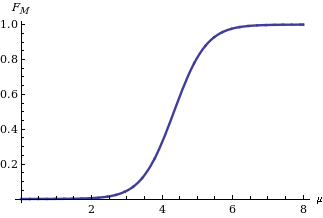
Реализация извилистый аргумент метод, вы получите закон распределения ${ Displaystyle F_ {M} ( mu)}$ среднего M гауссовой переменной Икс на основе статистики ${ displaystyle s_ {M} = sum _ {i = 1} ^ {m} x_ {i}}$ когда ${ displaystyle Sigma ^ {2}}$ как известно, равно ${ displaystyle sigma ^ {2}}$ (Аполлони, Мальчиоди и Гайто 2006). Его выражение:

${ Displaystyle F_ {M} ( mu) = Phi left ({ frac {m mu -s_ {M}} { sigma { sqrt {m}}}} right),}$

показано на рисунке справа, где ${ displaystyle Phi}$ это кумулятивная функция распределения из стандартное нормальное распределение.

Верхний (фиолетовая кривая) и нижний (синяя кривая) крайние значения 90% доверительного интервала среднего M гауссовой случайной величины для фиксированного ${ displaystyle sigma}$ и разные значения статистики s_м.

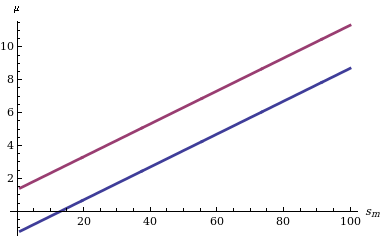
Вычисление доверительный интервал за M учитывая, что его функция распределения проста: нам нужно найти только два квантиля (например, ${ displaystyle delta / 2}$ и ${ displaystyle 1- delta / 2}$ квантилей в случае, если нас интересует доверительный интервал уровня δ, симметричный относительно вероятностей хвоста), как показано слева на диаграмме, показывающей поведение двух границ для разных значений статистики s_м.

Ахиллесова пята подхода Фишера заключается в совместном распределении более чем одного параметра, например среднего и дисперсии гауссова распределения. Напротив, при последнем подходе (и вышеупомянутых методах: бутстрап населения и извилистый аргумент) мы можем узнать совместное распределение многих параметров. Например, сосредоточив внимание на распределении двух или более параметров, на рисунках ниже мы сообщаем о двух доверительных областях, в которых функция, которую необходимо изучить, падает с достоверностью 90%. Первый касается вероятности того, что расширенный Машина опорных векторов присваивает двоичную метку 1 точкам ${ Displaystyle (х, у)}$ самолет. Две поверхности нарисованы на основе набора точек выборки, в свою очередь маркированных в соответствии с определенным законом распределения (Аполлони и др. 2008 г.). Последнее касается доверительной области вероятности рецидива рака молочной железы, рассчитанной на основе цензурированной выборки (Аполлони, Мальчиоди и Гайто 2006).

90% доверительная область для семейства машин опорных векторов, наделенных функцией профиля гиперболического тангенса

90% доверительный интервал для функции риска рецидива рака молочной железы, рассчитанный на основе цензурированной выборки ${ Displaystyle t = (9,13,> 13,18,12,23,31,34,> 45,48,> 161), ,}$ с>т обозначая цензуру время

Примечания

Эта статья включает в себя список общих Рекомендации, но он остается в основном непроверенным, потому что ему не хватает соответствующих встроенные цитаты. Пожалуйста, помогите улучшать эта статья введение более точные цитаты. (Июль 2011 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Рекомендации

• Фрейзер, Д. А. С. (1966), "Структурная вероятность и обобщение", Биометрика, 53 (1/2): 1–9, Дои:10.2307/2334048, JSTOR 2334048.CS1 maint: ref = harv (связь)
• Фишер, М. А. (1956), Статистические методы и научные выводы, Эдинбург и Лондон: Оливер и БойдCS1 maint: ref = harv (связь)
• Apolloni, B .; Malchiodi, D .; Гайто, С. (2006), Алгоритмический вывод в машинном обучении, Международная серия по расширенному интеллекту, 5 (2-е изд.), Аделаида: Мэджилл, Advanced Knowledge InternationalCS1 maint: ref = harv (связь)
• Apolloni, B .; Bassis, S .; Malchiodi, D .; Витольд, П. (2008), Загадка гранулярных вычислений, Исследования в области вычислительного интеллекта, 138, Берлин: Springer, ISBN 9783540798637CS1 maint: ref = harv (связь)
• Рэмси, Ф. П. (1925), "Основы математики", Труды Лондонского математического общества: 338–384, Дои:10.1112 / плмс / с2-25.1.338.CS1 maint: ref = harv (связь)
• Уилкс, С.С. (1962), Математическая статистика, Статистические публикации Wiley, Нью-Йорк: Джон ВилиCS1 maint: ref = harv (связь)