WikiDer > Алфавитная система счисления
| Системы счисления |
|---|
| Индусско-арабская система счисления |
| Восточная Азия |
| Европейский |
| Американец |
| По алфавиту |
| Бывший |
| Позиционные системы к основание |
| Нестандартные позиционные системы счисления |
| Список систем счисления |
An буквенная система счисления это тип система счисления. Разработано в классическая древность, он процветал в раннее средневековье.[1] В буквенных системах счисления числа написаны с использованием символы из алфавит, слоговое письмо, или другой система письма. В отличие от акрофонические системы счисления, где числительное представлено первой буквой лексического названия числительного, буквенные системы счисления могут произвольно назначать буквы числовым значениям. Некоторые системы, в том числе арабский, Грузинский и иврит систем, используйте уже установленные Алфавитный порядок.[2] Алфавитные системы счисления возникли с Греческие цифры около 600 г. до н.э. и в значительной степени вымер к 16 веку.[3] После разработки позиционная цифра такие системы, как Индусско-арабские цифры, использование буквенных систем счисления сократилось до преимущественно упорядоченных списков, разбивка на страницы, религиозные функции и гадательная магия.[4]
История
Первая аттестованная буквенная система счисления - это Греческий алфавит система (названная Ионный или же Милезский система из-за ее происхождения на западе Малая Азия). Структура системы повторяет структуру Египетские демотические цифры; Греческие буквы заменили египетские знаки. Первые образцы греческой системы датируются 6 веком до нашей эры и написаны буквами архаичное греческое письмо используется в Иония.[5]
Другие культуры, контактировавшие с Грецией, приняли это числовое обозначение, заменив греческие буквы своим собственным письмом; в их число входили евреи в конце 2 века до нашей эры. В Готический алфавит приняли свои буквенные цифры наряду с греческим сценарием.[6] В Северная Африка, то Коптская система был разработан в 4 веке нашей эры,[7] и Ge'ez Система в Эфиопии была разработана около 350 года нашей эры.[8] Оба были разработаны на основе греческой модели.
Арабы разработали свою собственную буквенную систему счисления, абджад цифры, в 7 веке нашей эры, и использовал его в математических и астрологических целях даже в 13 веке, намного позже введения Индусско-арабская система счисления.[9] После принятия христианства Армяне и Грузины разработали свою алфавитную систему счисления в 4 или начале 5 века, а в Византийская империя Кириллические цифры и Глаголица были введены в 9 веке. Алфавитные системы счисления были известны и использовались на севере, в Англии, Германии и России, на юге, в Эфиопии, на востоке, в Персии, и в Северной Африке, от Марокко до Центральной Азии.[нужна цитата]
К XVI веку нашей эры большинство алфавитных систем счисления вымерли или мало использовались, вытесненные Арабский позиционный и Западные цифры как обычные цифры торговли и управления по всей Европе и на Ближнем Востоке.[10]
Новейшие используемые буквенные системы счисления, все они позиционные, являются частью систем тактильного письма для слабовидящий. Хотя 1829 шрифт Брайля у него была простая зашифрованная позиционная система, скопированная с западных цифр с отдельным символом для каждой цифры, ранний опыт работы со студентами заставил ее разработать Луи Брайля чтобы упростить систему, доведя количество доступных шаблонов (символов) со 125 до 63, ему пришлось перепрофилировать дополнительный символ, чтобы обозначить буквы a – j как цифры. Помимо этой традиционной системы, другой был разработан во Франции в 20 веке, и еще один в США.
Системы
В алфавитной системе счисления используется буквы скрипта в определенном порядке алфавита для обозначения цифр.
В греческом языке буквы назначаются соответствующим числам в следующих наборах: от 1 до 9, от 10 до 90, от 100 до 900 и так далее. Десятичные разряды представлены одним символом. По мере того как алфавит заканчивается, более высокие числа представляются с помощью различных методов умножения. Однако, поскольку системы письма имеют разное количество букв, другие системы письма не обязательно группируют числа таким образом. В Греческий алфавит имеет 24 буквы; нужно было добавить еще три буквы, чтобы получить 900. В отличие от греческого, Еврейский алфавит22 буквы разрешены для числового выражения до 400. Арабский абджад28 согласных знаков могли представлять числа до 1000. В древних арамейских алфавитах было достаточно букв, чтобы достигать 9000. В математических и астрономических рукописях для представления больших чисел использовались другие методы. римские цифры и Чердачные цифрыобе системы были также алфавитно-цифровыми, со временем стали более лаконичными, но требовали, чтобы их пользователи знали гораздо больше знаков. Акрофонический цифры не принадлежат к этой группе систем, потому что их буквенно-цифровые символы не соответствуют порядку алфавита.
У этих различных систем нет единой объединяющей черты или особенности. Наиболее распространенная структура - это зашифрованная аддитивная структура с десятичным основанием, с использованием или без использования мультипликативно-аддитивной структуры для более высоких чисел. Исключения включают армянскую нотацию Ширакаци, который является мультипликативно-аддитивным и иногда использует основание 1000, а также греческую и арабскую системы астрономической записи.
Цифровые знаки
В таблицах ниже показаны буквенно-цифровые конфигурации различных систем письма.
Греческие буквенные цифры - «ионийские» или «милетские числа» - (крошечные буквы)
единицы α β γ δ ε ϛ ζ η θ 1 2 3 4 5 6 7 8 9 десятки ι κ λ μ ν ξ ο π ϟ 10 20 30 40 50 60 70 80 90 сотни ρ σ τ υ φ χ ψ ω ϡ 100 200 300 400 500 600 700 800 900 тысячи ͵α ͵β ͵γ ͵δ ͵ε ͵ϛ ͵ζ ͵η ͵θ 1000 2000 3000 4000 5000 6000 7000 8000 9000
Некоторые числа представлены Греческие буквенные цифры:
- ͵γϡμβ = (3000 + 900 + 40 + 2) = 3942
- χξϛ = (600 + 60 + 6) = 666
единицы א ב ג ד ה ו ז ח ט 1 2 3 4 5 6 7 8 9 десятки י כ ל מ נ ס ע פ צ 10 20 30 40 50 60 70 80 90 сотни ק ר ש ת 100 200 300 400 тысячи 'א 'ב 'ג 'ד 'ה 'ו 'ז 'ח 'ט 1000 2000 3000 4000 5000 6000 7000 8000 9000
В системе письма иврита всего двадцать четыре согласных знака, поэтому числа могут быть выражены отдельными знаками только до 400. Более высокие сотни - 500, 600, 700, 800 и 900 - могут быть записаны только с помощью различных совокупно-аддитивных комбинаций. младших сотен (направление письма справа налево):[11]
- תק = (400+100) 500
- תר = (400+200) 600
- תש = (400+300) 700
- תת = (400+400) 800
- תררק = 400+200+200+100 = 900
Армянская цифра знаки (крохотные буквы):
единицы ա բ գ դ ե զ է ը թ 1 2 3 4 5 6 7 8 9 десятки ժ ի լ խ ծ կ հ ձ ղ 10 20 30 40 50 60 70 80 90 сотни ճ մ յ ն շ ո չ պ ջ 100 200 300 400 500 600 700 800 900 тысячи ռ ս վ տ ր ց ւ փ ք 1000 2000 3000 4000 5000 6000 7000 8000 9000 десять тысяч օ ֆ 346 = յ
В отличие от многих алфавитных систем счисления, армянская система не использует умножение на 1 000 или 10 000 для выражения более высоких значений. Вместо этого более высокие значения записывались полностью с использованием лексических числительных.[12]
Высшие числа
По мере того как алфавит заканчивался, для выражения более высоких чисел в разных системах использовались различные методы умножения. В греческой алфавитной системе для числа, кратного 1000, Хаста Знак был помещен слева под числовым знаком, чтобы указать, что его следует умножить на 1000.[13]
- β = 2
- ͵β = 2,000
- ͵κ = 20,000
С помощью второго уровня мультипликативного метода - умножения на 10 000 - набор чисел может быть расширен. Самый распространенный метод, используемый Аристарх, включал размещение числовой фразы над большим символом M (M = мириады = 10 000), чтобы указать умножение на 10 000.[14] Этот метод может выражать числа до 100000000 (108).
20,704 − (2 ⋅ 10,000 + 700 + 4) можно представить как:
ψδ = 20,704
В соответствии с Папп Александрийскийотчет, Аполлоний Пергский использовал другой метод. В нем цифры над M = мириады = 10 000 представляют показатель степени 10 000. Число, которое нужно умножить на M, было написано после символа M.[15] Этот метод мог выразить 5,462,360,064,000,000 в качестве:
͵EYZB ͵ΓX ͵FY 100003 × 5462 + 100002 × 3600 + 100001 × 6400
Как отличить числовые фразы от текста
Буквенные цифры отличались от слов со специальными знаками, чаще всего горизонтальной чертой над числовой фразой, но иногда с точками, помещенными по обе стороны от нее. Последнее проявилось в греческом алфавите с Хаста знак.
В Эфиопские цифры, известный как Geʽez, знаки имеют отметки как над, так и под ними, чтобы указать, что их значение является числовым. Исключением являются эфиопские цифры, где цифровые знаки не являются буквами их письменности. Эта практика стала повсеместной с 15 века.[16]
Цифровые знаки эфиопских цифр с отметками как над, так и под буквами:
1 2 3 4 5 6 7 8 9 × 1 ፩ ፪ ፫ ፬ ፭ ፮ ፯ ፰ ፱ × 10 ፲ ፳ ፴ ፵ ፶ ፷ ፸ ፹ ፺ × 100 ፻ × 10,000 ፼
Направление цифр соответствует направлению системы письма. На греческом, коптском, эфиопском, готическом, армянском, грузинском, глаголице и кириллице буквы пишутся слева направо, а также используются обозначения Ширакаци. Написание справа налево встречается в еврейских и сирийских буквенных цифрах, арабских цифрах абджад и цифрах Феса.[нужна цитата]
Фракции
Дроби единицы
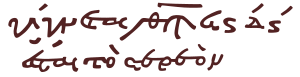
Дроби единицы были методом выражения дробей. В греческой алфавитной записи дроби единиц обозначались знаменателем - буквенным цифровым знаком, за которым следовали небольшие акценты или штрихи, помещенные справа от цифры, известной как Керая (ʹ). Следовательно, γʹ указал одну треть, δʹ одна четверть и так далее. Эти фракции были аддитивными и также назывались Египетские фракции.
Например: δ´ ϛ´ =1⁄4 + 1⁄6 = 5⁄12.
Смешанное число можно записать так: ͵θϡϟϛ δ´ ϛ´ = 9996 + 1⁄4 + 1⁄6
Астрономические дроби
Во многих астрономических текстах отдельный набор алфавитных систем счисления смешивает их обычные алфавитные цифры с основанием 60, например Вавилонские шестидесятеричные системы. Во II веке до нашей эры появился гибрид вавилонской системы обозначений и греческих буквенных цифр, который использовался для выражения дробей.[17] В отличие от вавилонской системы, греческое основание 60 не использовалось для выражения целых чисел.
С этим шестидесятеричный позиционный система - с суббазой 10 - для выражения фракциибыли использованы четырнадцать буквенных цифр (единицы от 1 до 9 и декады от 10 до 50), чтобы написать любое число от 1 до 59. Это могло быть числитель дроби. Позиционный принцип использовался для знаменателя дроби, который был записан с показателем 60 (60, 3 600, 216 000 и т. Д.). Шестидесятеричные дроби могут использоваться для выражения любого дробного значения с последовательными позициями, представляющими 1/60, 1/60.2, 1/603, и так далее.[18] Первым основным текстом, в котором появилась эта смешанная система, был Птолемейс Альмагест, написано во 2 веке нашей эры.[19]
Астрономические дроби (с греческими буквенными знаками):
единицы α β γ δ ε ϛ ζ η θ 1 2 3 4 5 6 7 8 9 десятки ι κ λ μ ν 10 20 30 40 50
͵αφιε κ ιε = 1515 + (20 х 1/60) + (15 х 1/3600) = 1515.3375
Эта смешанная система не использовала точка счисления, но у астрономических дробей был специальный знак для обозначения нуля в качестве заполнителя. В некоторых поздневавилонских текстах использовался аналогичный заполнитель. Греки переняли эту технику, используя свой собственный знак, форма и характер которого со временем изменились от ранних манускриптов (I век нашей эры) до буквенного обозначения.[20]
Это шестидесятеричное обозначение было особенно полезно в астрономии и математике из-за деления круга на 360 градусов (с делениями по 60 минут на градус и 60 секунд в минуту). В Теон Александрийскийкомментарий к Альмагесту (IV век н.э.), числовая фраза ͵αφιε κ ιε выражает 1515 (͵αφιε) градусов, 20 (κ) минут и 15 (ιε) секунд.[21] Значение градуса выражается обычными десятичными буквенными числами, включая использование мультипликативного числа. Хаста на 1000, а последние две позиции записаны шестидесятеричной дробью.
Арабы переняли астрономические дроби непосредственно у греков, и точно так же иудейские астрономы использовали шестидесятеричные дроби, но греческие числовые знаки были заменены их собственными буквенными цифровыми знаками, чтобы выражать как целые числа, так и дроби.
Буквенные системы счисления
- Цифры абджад
- Армянские цифры
- Āryabhaa нумерация
- Чердачные цифры
- Коптские цифры
- Кириллические цифры
- Эфиопские цифры
- Цифры фес
- Глаголические цифры
- Грузинские цифры
- Готические цифры
- Греческий алфавит
- Цифры на иврите
- римские цифры
- Система счисления Ширакаци
- Сирийские буквенные цифры
Рекомендации
- ^ Стивен Хрисомалис (2010). Числовые обозначения: сравнительная история. Издательство Кембриджского университета. п. 185. ISBN 9780521878180. Получено 2019-10-02.
- ^ Стивен Хрисомалис (2010). Числовые обозначения: сравнительная история. Издательство Кембриджского университета. п. 185. ISBN 9780521878180. Получено 2019-10-02.
- ^ Стивен Хрисомалис (2010). Числовые обозначения: сравнительная история. Издательство Кембриджского университета. п. 185. ISBN 9780521878180. Получено 2019-10-02.
- ^ Стивен Хрисомалис (2010). Числовые обозначения: сравнительная история. Издательство Кембриджского университета. п. 185. ISBN 9780521878180. Получено 2019-10-02.
- ^ С. Хрисомалис (2010), стр. 135–138.
- ^ С. Хрисомалис (2010) стр. 155.
- ^ С. Хрисомалис (2010) стр. 148.
- ^ С. Хрисомалис (2010) стр. 152.
- ^ С. Хрисомалис (2010) с.166.
- ^ С. Хрисомалис (2010) стр. 185.
- ^ С. Хрисомалис (2010) стр. 156
- ^ С. Хрисомалис (2010) стр. 174.
- ^ С. Хрисомалис (2010) стр. 138
- ^ Хит, Томас Л. (1921). История греческой математики. 2 тома. Кембридж: Издательство Кембриджского университета. С. 39–41.
- ^ Греческие системы счисления - MacTutor
- ^ Ифра (1998), стр. 246–247.
- ^ Ifrah (1998) стр. 156.
- ^ С. Хрисомалис (2010) стр. 169)
- ^ Хит (1921), стр. 44–45.
- ^ Иранский 1955
- ^ Томас, Айвор. 1962 г. Избранные, иллюстрирующие историю греческой математики, т. 1. Кембридж, Массачусетс: Издательство Гарвардского университета. С. 50–51.
Источники
- Стивен Хрисомалис (2010). Числовые обозначения: сравнительная история. Издательство Кембриджского университета. С. 133–187. ISBN 9780521878180.
- Жорж Ифра (1998). Универсальная история чисел: от предыстории до изобретения компьютера; перевод с французского Давида Беллоса. Лондон: Harvill Press. ISBN 9781860463242.
- Хит, Томас Л. (1921). История греческой математики. 2 тома. Кембридж: Издательство Кембриджского университета.
- Отто Нойгебауэр (1979). Эфиопская астрономия и компьютерные науки. Вена: Verlag der Österreichischen Akademie der Wissenschaften.
- Мегалли, Фуад (1991). Система счисления, коптский. Коптская энциклопедия, Азис С. Атия, изд.. Нью-Йорк: Макмиллан. С. 1820–1822..
- Мессиха, Хешмат. 1994. Les chiffres coptes. Le Monde Copte 24: 25–28.
- Брауне, Вильгельм и Эрнст Эббингаузы. 1966 г. Gotische Grammatik. Тюбинген: Макс Нимейер Верлаг.
- Гандз, Соломон. 1933. Еврейские цифры. Труды Американской академии еврейских исследований 4: 53–112.
- Миллард, А. 1995. Чужеземцы из Египта и Греции - знаки для чисел на раннем иврите. В Иммиграция и эмиграция на Древнем Ближнем Востоке, K. van Lerberghe and A. Schoors, eds., Pp. 189–194. Лёвен: Петерс.
- Колин, Г.С. 1960. Абджад. В Энциклопедия ислама, т. 1. С. 97–98. Лейден: Брилл.
- Колин Г.С. 1971. Хисаб аль-Джуммал. В Энциклопедия ислама, т. 3, стр. 468. Лейден: Brill.
- Бендер, Марвин Л., Сидней В. Хед и Роджер Коули. 1976. Эфиопская письменность. В Язык в Эфиопии, М.Л. Бендер, Дж.Д. Боуэн, Р.Л. Купер и К.А. Ferguson, eds., Pp. 120–129. Лондон: Издательство Оксфордского университета.
- Шоу, Аллен А. 1938–199. Заброшенная античная система счисления. Национальный математический журнал 13: 368–372.
- Кубберли, Пол. 1996. Славянские алфавиты. В Системы письма мира, Питер Т. Дэниэлс и Уильям Брайт, ред., Стр. 346–355. Нью-Йорк: Издательство Оксфордского университета.
- Панкхерст, Ричард К. П., изд. 1985 г. Письма эфиопских правителей (начало и середина девятнадцатого века), переведенный Дэвидом Л. Эпплярдом и А.К. Ирвин. Оксфорд: Издательство Оксфордского университета.
- Смит, Дэвид Э. и Л. Карпински. 1911 г. Индо-арабские цифры. Бостон: Джинн
- Гандз, Соломон. 1933. Еврейские цифры. Труды Американской академии еврейских исследований 4. С. 53–112.
- Шанцлин, Г. Л. 1934. Обозначение абджад. Мусульманский мир 24: 257–261.



